Дискретизация сигналов. Теорема В.А. Котельникова.

 

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми (analog). Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом (discrete series) и не может полностью соответство­вать аналоговому сигналу. Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала (samples). Как правило, отсчеты берутся через равные про­межутки времени Т, называемые периодом дискретизации (или интервалам, ша­гом дискретизации — sample time). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency): f_Д=1/Т. Соответст­вующая ей круговая частота определяется следующим образом: ω_Д=2π/Т.

Процесс преобразования аналогового сигнала в последовательность от счетов на­зывается дискретизацией (sampling), а результат такого преобразования — дискретным сигналом.

При обработке сигнала в вычислительных устройствах его отсчеты представля­ются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследст­вие этого отсчеты могут принимать лишь конечное множество значений и, сле­довательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню (quantization), а возникающие при этом ошибки округления — ошибками (или шумами) квантования (quantization error, quantization noise). Сигнал, дискретный во времени, но не квантованный по уровню, называется дис­кретным (discrete-time) сигналом. Сигнал, дискретный во времени и квантован­ный по уровню, называют цифровым (digital) сигналом. Сигналы, квантованные по уровню, но непрерывные во времени, на практике встречаются редко. Раз­ницу между аналоговыми, дискретными и цифровыми сигналами иллюстрирует рис. 7.1.

 

 

 

Рисунок 7.1. Аналоговый, дискретный и цифровой сигналы.

 

 

Процесс преобразования аналогового сигнала в цифровой предполагает последовательное выполнение следующих операций:

1. выборка значений исходной аналоговой величины в некоторые наперед заданные дискретные моменты времени, т. е. дискретизация сигнала по времени;

2. квантование (округление до некоторых известных величин) полученной в дискретные моменты време­ни последовательности значений исходной аналого­вой величины по уровню;

3. кодирование — замена найденных квантованных значений некоторыми числовыми кодами.

Пусть задана некоторая аналоговая зависимость U(t). Для получения ее дискретного эквивалента U(nТ_Д) = {U(0), U(Т_Д), U(2Т_Д),... } необходимо провести выборку ее значе­ний в дискретные моменты времени nТ_Д,, где n = 0, 1, 2... целое число. Постоянная величина Т_Д— носит название пе­риода выборки или периода дискретизации, а сам процесс замены исходной аналоговой функции u(t) некоторой диск­ретной функцией U(nТ_Д)называется дискретизацией сигна­ла во времени. Следует отметить, что полученная дискрет­ная функция U(nТ_Д)относительно самого сигнала U(t) но­сит по-прежнему аналоговый характер, так как может при­нимать бесконечное число различных значений.

Период дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью.

При выборе периода дискретизации можно воспользоваться теоремой В.А.Котельникова, согласно которой всякий непре­рывный сигнал, имеющий ограниченный частотный спектр, пол­ностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервалы времени:

Т_д = 1/2F_max,

где F_max – максимальная частота в частотном спектре сигнала.

Дискретизация по времени не связана с потерей информа­ции, если частота дискретизации f_Д=1/Т_Д в 2 раза выше максимальной частоты сигнала F_max. Однако почти все сигналы, используемые на практике, имеют неограниченный по частоте спектр, поэтому теорема Котельникова учитывает лишь 90% спектра сигнала. Для неограниченного по частоте спектра частоту дискретизации увеличивают в 2-3 раза:

f_Д = (2÷3)*2 F_max = (4÷6) F_max

Для устранения недостатка теоремы Котельникова применяют критерий Железнова (вы­полняется для случайных сигналов, имеющих конечную дли­тельность Т и неограниченный частотный спектр), в соответствии с которым рекоменду­ется принимать период дискретизации Т_Д, равный максимальному интервалу корреляции сигнала τ₀, т.е.

Т_Д = τ₀

Параметр τ₀ характеризует такой промежуток времени, в пре­делах которого отдельные значения случайного процесса можно считать статистически зависимыми (коррелированными). Таким образом, исходный непрерывный сигнал заме­няется совокупностью W = Т/τ₀ некоррелированных отсчетов (выборок), следующих с частотой

f_Д = 1/ Т_Д = 1/τ₀.

Кроме временной дискретизации необходимо производить еще квантование выборочных значений сигнала. Поскольку математической моделью непрерывного сиг­нала является случайный процесс U(t), мгновенные значения сигнала U_k = U(t_k) представляют собой случайную величину. Диапазон ее изменения, называемый непрерывной шкалой мгно­венных значений сигнала, ограничен значениями U_min и U_max, что отражает условие физической реализуемости сигнала. Не­прерывную шкалу мгновенных значений U_max – U_min сигнала разбивают на m уровней. Отличительной особенностью дискре­тизации по уровню является замена непрерывной шкалы уров­ней сигнала U(t) дискретной шкалой Ū_к{ к = 1,2,...,М), в которой различные значения сигнала отличаются между собой на некоторое фиксированное (или выбираемое в процессе квантования) значение ΔU, называемое шагом квантования. Таким образом, квантование представляет собой округление мгновен­ных значений преобразуемого сигнала. При равномерном кван­товании (ΔU = const) число разрешенных дискретных уровней составляет

Чем больше шаг квантования, тем больше получается ошибка – шум квантования:

ξ(U) = U_к - Ū_к .

Если в результате квантования любое из мгновенных значений сигнала U(t) оказалось в интервале

(Ū_к – ΔU/2; Ū_к + ΔU/2),

то оно округляется до Ū, а возникающая при этом ошибка

| ξ(U)|_max = ΔU/2.

 

 

 

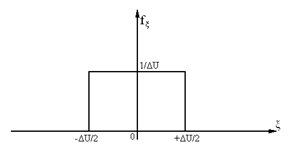
Рисунок 7.2. Выбор шага квантования сигнала

 

На практике ΔU выбирают следующим методом. Полагают ошибку квантования ξ(U) случайной величиной, подчиненной равномер­ному закону распределения. Плотность вероятности f(ξ) для случайной величины ξ принимает значение внутри интервала (– ΔU/2; + ΔU/2) и равна нулю вне этого интервала.

Дисперсия D[ξ] ошибки квантования ξ определяется как

Для выполнения последней операции необходимо выб­рать некоторый код К = {K_1, К₂,...}, способный отобра­жать не менее (N+1)-го значения, и каждому дискретно­му значению Ū_к поставить в соответствие некоторый код K_i. В простейшем случае в качестве кода может быть ис­пользована последовательность чисел, соответствующих по­рядковым номерам уровней квантования. При таком выбо­ре кода функция U(t)может быть заменена последова­тельностью десятичных чисел: Кn= {0, 1, 3, 4, 4, 5, 4, 4, 3, 2, 2}, или в двоичной форме Кn = {000, 001, 011, 100, 100, 101, 100, 100, 011, 010, 010}.

Р.Хартли предложил в качестве меры количества информа­ции использовать логарифм числа возможных сообщений

I = W log_a m,

Согласно этому логарифму, количество информации в дискретном сигнале зависит от числа отсчётов W= Т/τ₀ и от числа уровней квантования m.

Часто принимают а = 2, при этом значение I измеряется в битах.

Количество информации, приходящееся на один отсчет сигнала, называют удельной информативностью сигнала, или энтропией сигнала

H = I/W.

Энтропия является мерой неопределенности исследуемого процесса.