При минимизации по методу Квайна (базис 1)предполагается, что исходная функция задана в СДНФ.
Импликанта функции – некая логическая функция, обращаемая в нуль при наборе переменных, на котором сама функция также равна нулю. Поэтому любой конъюнктивный терм, входящий в состав СДНФ, или группа термов, соединенных знаками дизъюнкции, является импликантами исходной ДНФ.
Первичная импликанта функции – импликанта типа элементарной конъюнкции некоторых переменных, никакая часть которой не является импликантой.
Задача минимизации по методу Квайна состоит в попарном сравнении всех импликант, входящих в СНДФ, с целью выявления возможности поглощения какой – то переменной:
 (2.6)
(2.6)
Таким образом, удается снизить ранг термов. Эта процедура проводится до тех пор, пока не остается ни одного члена, допускающего поглощение с каким-либо другим термом. Термы, подвергшиеся поглощению, отмечаются. Неотмеченные термы переставляют собой первичные импликанты.
Полученное логическое выражение не всегда оказывается минимальным. Поэтому исследуется возможность дальнейшего упрощения. Для этого составляется таблица, в строках которой записываются найденные первичные импликанты, а в столбцах указываются термы исходного управления. Клетки этой таблицы отмечаются в случае, если первичная импликанта входит в состав какого-либо терма. После этого задача упрощения сводится к тому, чтобы найти минимальное количество первичных импликант, которые совместно покрывают все столбцы.
Метод Квайна выполняется в несколько этапов, рассмотрим его применение на конкретном примере
Пусть необходимо минимизировать логическую функцию, заданную в виде 
Задача решается в несколько этапов.
Этап 1. Нахождение первичных импликант. Прежде всего составляется таблица (табл.2.3) и находятся импликанты четвертого и третьего ранга, т.е. снижается ранг членов, входящих в СДНФ.
Таблица 2.3
| Исходные термы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 (0011)
(0011)
|
|
|
| 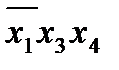
|
| 
|
|
|
 (0100)
(0100)
|
|
| 
|
|
|
| 
|
|
 (0101)
(0101)
|
| 
|
| 
|
|
|
| 
|
 (0111)
(0111)
| 
|
| 
|
|
|
|
|
|
 (1001)
(1001)
|
|
|
|
|
| 
|
| 
|
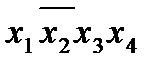 (1011)
(1011)
| 
|
|
|
| 
|
|
|
|
 (1100)
(1100)
|
| 
|
|
|
|
|
| 
|
 (1101)
(1101)
|
|
| 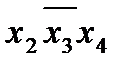
|
| 
|
| 
|
|
Затем составляется другая таблица, которая включает все термы, не подвергшиеся поглощению, а также первичные импликанты третьего ранга. Составление таблиц продолжается до тех пор, пока нельзя будет применять правило. В рассматриваемом примере можно дойти до первичной импликанты второго ранга – х2.х3
Первичные импликанты наименьшего ранга выделены в табл.2.4:
Таблица 2.4
| Первичные импликанты ранга 3
| 
| 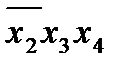
| 
| 
| 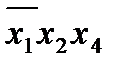
| 
| 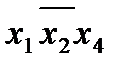
| 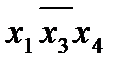
| 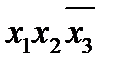
|

|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
| 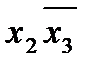
|

|
|
|
|
|
| х2.х3
|
|
|
|

|
|
|
|
|
|
|
|
|
|
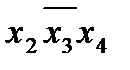
|
|
|
| 
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этап 2. Расстановка меток. Составляется таблица, число строк которой равно числу полученных первичных импликант, а число столбцов совпадает с числом минтермов СНДФ. Если в некоторый минтерм СНДФ входит какая-либо из первичных импликант, то на пересечении соответствующего столбца и строки становится метка (табл.2.5):
Таблица 2.5
| Первичные
импликанты
|
|
|
|
|
|
|
|
|
| Исходные термы
|
|
|
|
|
|
|
|
|
|

| Ú
|
|
| Ú
|
|
|
|
|
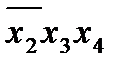
| Ú
|
|
|
|
| Ú
|
|
|
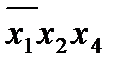
|
|
| Ú
| Ú
|
|
|
|
|

|
|
|
|
| Ú
| Ú
|
|
|

|
|
|
|
| Ú
|
| Ú
| Ú
|

|
| Ú
| Ú
|
|
|
| Ú
| Ú
|
Этап 3.Нахождение существенных импликант. Если в каком-либо из столбцов в таблице, представленной выше, имеется только одна метка, то первичная импликанта в соответствующей строке является существенной, так как без нее не будет получено все множество заданных минтермов. В таблице существенной импликантой является терм  . Столбцы, соответствующие существенным импликантам, из таблицы вычеркивается.
. Столбцы, соответствующие существенным импликантам, из таблицы вычеркивается.
Этап 4. Вычеркивание лишних столбцов. После третьего этапа в результате вычеркивания столбцов 2,3,7и 8 получается табл.2.6.
Таблица 2.6
| Первичные
импликанты
|
|
|
|
|
| Исходные термы
|
|
|
|
|
|

| Ú
| Ú
|
|
|
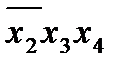
| Ú
|
|
| Ú
|
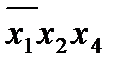
|
| Ú
|
|
|

|
|
| Ú
| Ú
|

|
|
| Ú
|
|
Если в таблице есть два столбца, в которых имеются метки в одинаковых строках, то один из них вычеркивается. Покрытие оставшегося столбца будет осуществлять отброшенный минтерм. В примере такого случае нет.
Этап 5. Вычеркивание лишних первичных импликант. Если после отбрасывания некоторых столбцов на этапе 4 в таблице, представленной выше появляются строки, в которых нет ни одной метки, то первичные импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, так как они не покрывают оставшиеся в рассмотрении минтремы.
Этап 6. Выбор минимального покрытия. Выбирается в таблице такая совокупность первичных импликант, которая включает метки во всех столбцах по крайней мере по одной метке в каждом столбце. При нескольких возможных вариантах такого выбора отдается предпочтение варианту покрытия с минимальным суммарным числом букв в импликантах, образующих покрытие. Этому требованию удовлетворяют первичные импликанты  и
и  .
.
Таким образом, минимальная форма заданной функции складывется из суммы существенных импликант (этап 3) и первичных импликант, покрывающих оставшиеся минтермы (этап 6):
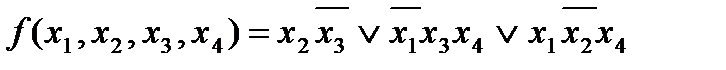 (2.7)
(2.7)
На основании изложенного, сформулируем алгоритм получения минимальных дизъюнктивных нормальных форм переключательной функции.
1. ПФ представляют в СДНФ. При этом если функция задана таблицей, то ее представляют в записи по единицам, если же функция задана в произвольной аналитической форме, то СДНФ можно получить применяя операции развертывания, правила Де-Моргана и формулы булевой алгебры.
2. В полученной СДНФ проводят все операции неполного склеивания и поглощения. В результате этого получается сокращенная ДНФ заданной функции.
3. Находят все минимальные ДНФ по импликантной матрице или методом испытания.





 (2.6)
(2.6)
 (0011)
(0011)
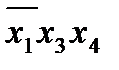

 (0100)
(0100)


 (0101)
(0101)



 (0111)
(0111)


 (1001)
(1001)


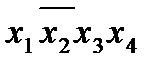 (1011)
(1011)


 (1100)
(1100)


 (1101)
(1101)
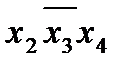



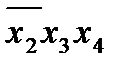


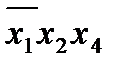

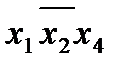
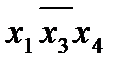
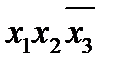



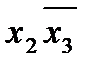


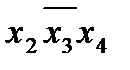





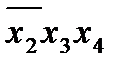
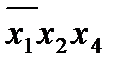

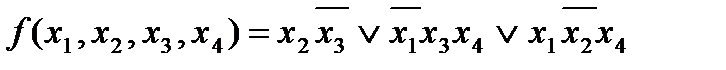 (2.7)
(2.7)

