При построении комбинационных схем (КС) с целью уменьшения затрат оборудования производится минимизация системы булевых функций, выполняемая обычно в 2 этапа. Сначала по канонической ДНФ системы булевых функций строится минимальная форма. Для этого используются методы Квайна-Мак-Класки и импликантных матриц, карты Карно и т.д. Затем по минимальной форме находится скобочная форма. Если схема И-НЕ, то используются специальные приемы преобразования булевых функций, позволяющие минимизировать затраты оборудования в схемах с учетом специфики функций, реализуемых логическими элементами. Минимальные скобочные представления булевых функций используются в качестве формы для построения комбинационной схемы.
Канонический метод синтеза КС покажем на следующем примере.
Пример. Пусть требуется синтезировать схему операционного элемента, реализующего ПФ
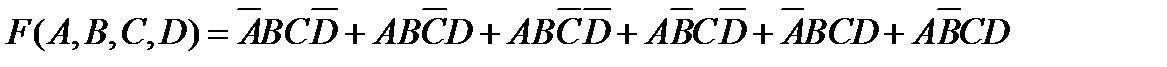
Выполним минимизацию этой ПФ с помощью карт Карно.
Минимальная форма ПФ имеет вид:

Реализация КС в базисе И, ИЛИ, НЕ представлена на рис.2.7

Рисунок 2.7 – Реализация КС в базисе И, ИЛИ, НЕ
Если для построения схемы используются элементы универсального базиса, реализующие операции И-НЕ, необходимо булевы функции перевести в базис И-НЕ. Этот перевод функций НЕ, И, ИЛИ выполняется по следующим формулам: (в базисе реализуется функция  ),
),

 (2.8)
(2.8)


Рисунок 2.8 – Реализация отрицания, конъюнкции и дизъюнкции в базисе И-НЕ
Реализация отрицания, конъюнкции и дизъюнкции в базисе И-НЕ показана на рис.2.8.
В соответствии со схемами и формулами, конъюнктивные термы  на выходах элементов И-НЕ будут определены инверсиями конъюнкций
на выходах элементов И-НЕ будут определены инверсиями конъюнкций  . Дизъюнкция термов вычисляется элементом И-НЕ, на входы которого поступают инверсии конъюнктивных термов. Схема, построенная по этому правилу, представлена на рис.2.9.
. Дизъюнкция термов вычисляется элементом И-НЕ, на входы которого поступают инверсии конъюнктивных термов. Схема, построенная по этому правилу, представлена на рис.2.9.

Рисунок 2.9 – Реализация КС в базисе И-НЕ
Схема, представленная на рис.2.9. незначительно отличается от рис.2.7.
Как показывает опыт, простая замена булевых функций на функции И-НЕ обычно не приводит к минимальным формам. Чтобы минимизировать затраты оборудования в схеме, необходимо минимизировать число инверсий над входными переменными по правилу:
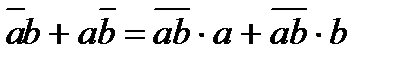

 (2.9)
(2.9)
Это правило позволяет выражение с двумя инверсиями 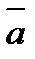 и
и  привести к выражению с единственной инверсией
привести к выражению с единственной инверсией 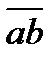 . С использованием этого правила ДНФ исходный ПФ преобразуется следующим образом:
. С использованием этого правила ДНФ исходный ПФ преобразуется следующим образом:


Рисунок 2.10 – Схема КС, преобразованной по методу уменьшения числа отрицаний
На рис.2.10 представлена схема, содержащая на 2 элемента меньше, чем эквивалентная ей схема рис.2.9.
Таким образом, при синтезе схем в базисе И-НЕ минимизация булевых функций проводится следующим образом:
1. Строятся минимальные ДНФ булевых функций;
2. Минимизируется число инверсий входных переменных на основе правила  ;
;
3. Дизъюнктивные формы переводятся в базис И-НЕ на основе соотношений (2.10).
Дополнительно следует отметить, что сокращение числа инверсий возможно только в случае если они имеют вид  , но не
, но не  .
.
Для реализации ПФ в базисе ИЛИ-НЕ необходимо по карте Карно-Вейча записать ее значение в конъюнктивной форме (по нулям) и преобразовать полученные выражения по правилу де Моргана к виду ИЛИ-НЕ. После этого не вызовет затруднений построить функциональную схему по полученному выражению.





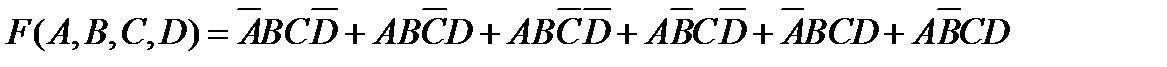

 ),
),
 (2.8)
(2.8)
 на выходах элементов И-НЕ будут определены инверсиями конъюнкций
на выходах элементов И-НЕ будут определены инверсиями конъюнкций  . Дизъюнкция термов вычисляется элементом И-НЕ, на входы которого поступают инверсии конъюнктивных термов. Схема, построенная по этому правилу, представлена на рис.2.9.
. Дизъюнкция термов вычисляется элементом И-НЕ, на входы которого поступают инверсии конъюнктивных термов. Схема, построенная по этому правилу, представлена на рис.2.9.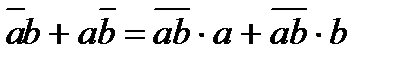

 (2.9)
(2.9) и
и  привести к выражению с единственной инверсией
привести к выражению с единственной инверсией  . С использованием этого правила ДНФ исходный ПФ преобразуется следующим образом:
. С использованием этого правила ДНФ исходный ПФ преобразуется следующим образом:
 ;
; , но не
, но не  .
.


