Геометрическая интерпретация задач линейного программирования дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. Задачи с двумя переменными всегда можно решить графически. Однако уже в трёхмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трёх, графическое решение невозможно.
Пусть дана задача
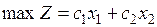 , (1)
, (1)
 , (2)
, (2)
 . (3)
. (3)
Каждое из ограничений (2) и (3) задает на плоскости  некоторую полуплоскость. Полуплоскость – выпуклое множество. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи есть выпуклое множество.
некоторую полуплоскость. Полуплоскость – выпуклое множество. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи есть выпуклое множество.
Пусть область допустимых решений – непустое множество, например многоугольник A 1 A 2 A 3 A 4 A 5 (рис. 3.4).

Рис. 3.4. Схема поиска решения задачи
графо-аналитическим методом
Выберем произвольное значение целевой функции Z = Z 0. Получим с 1 х 1 + с 2 х 2 = Z 0. Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение Z 0. Считая в равенстве (1) Z параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
Найдём частные производные целевой функции по х 1 и х 2:
 (4),
(4),  (5).
(5).
Частные производные (4) и (5) функции показывают скорость её возрастания вдоль соответствующих осей. Следовательно, с 1 и с 2 – скорости возрастания Z вдоль осей Oх 1 и Oх 2. Вектор с = (с 1, с 2) называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
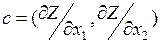 .
.
Вектор с указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор с = (с 1, с 2) перпендикулярен к прямым Z = const семейства с 1 х 1 + с 2 х 2 = Z.
Из геометрической интерпретации элементов задачи вытекает общий порядок её графического решения:
1) с учетом системы ограничений строим область допустимых решений;
2) определяем вектор с = (с 1, с 2) наискорейшего возрастания целевой функции, т. е. вектор градиентного направления;
3) проводим произвольную линию уровня Z = Z 0;
4) при решении задачи на максимум перемещаем линию уровня Z = Z 0 в направлении вектора  так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня Z = Z 0 перемещают в антиградиентном направленииж
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня Z = Z 0 перемещают в антиградиентном направленииж
5) определяем оптимальное решение х * = (х 1*, х 2*) и экстремальное значение целевой функции Z * = z (x *).
Пример. Найти оптимальные значения переменных х 1 и х 2, доставляющих максимум целевой функции
у = х 1 + 2 х 2 ® max,
при ограничениях на значения переменных
2 х 1 + х 2 £ 10, х 1 + 3 х 2 £ 18, х 1 ³ 0, х 2 ³ 0.
Для формирования области допустимых решений ОДР необходимо в системе координат х 1O х 2 построить линии, соответствующие ограничениям, приравнивая их левые и правые части, и определить направления расположения допустимых значений искомых переменных в соответствии со знаками неравенств (рис. 3.5).
Вычисления для построения первых двух ограничений:
2 х 1 + х 2 £ 10 ® 2 х 1 + х 2 = 10 Þ х 2 = 10 – 2 х 1;
х 1 + 3 х 2 £ 18 ® х 1 + 3 х 2 = 18 Þ х2 = (18 – х1) / 3;

Рис. 3.5. Область допустимых решений задачи
В соответствии с третьим ограничением значения переменной х 1 должны находиться выше оси Ох 2, а в соответствии с четвертым ограничением значения переменной х 2 должны находиться правее оси Ох 1. Следует иметь в виду, что границы ОДР в область допустимых решений входят.
Для окончательного определения оптимальных значений переменных х 1 и х 2 необходимо сначала построить произвольную прямую для целевой функции, приравняв её выражение к любому числу, так, чтобы эта прямая располагалась в пределах выбранного масштаба рисунка. Приравняем выражение целевой функции, например, к числу «16» и построим соответствующую прямую линию.
у = х 1 + 2 х 2 ® max; х 1 + 2 х 2 = 16 Þ х2 = (16 – х1) / 2;
После этого необходимо построить прямую линию, параллельную данной прямой, так, чтобы она коснулась границы ОДР. Координаты точки касания этой прямой с границей ОДР будут оптимальными значениями переменных х 1опт и х 2опт.
Для точного определения координат точки касания линии целевой функции границы ОДР необходимо решить систему, включающую в себя два уравнения: 2 х 1 + х 2 = 10 и х 1 + 3 х 2 = 18. При этом максимальное значение целевой функции у max = х 1 + 2 х 2 = 2,4 + 2 × 5,2 = 12,8.





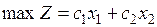 , (1)
, (1) , (2)
, (2) . (3)
. (3) некоторую полуплоскость. Полуплоскость – выпуклое множество. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи есть выпуклое множество.
некоторую полуплоскость. Полуплоскость – выпуклое множество. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи есть выпуклое множество.
 (4),
(4), 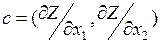 .
. так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня Z = Z 0 перемещают в антиградиентном направленииж
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня Z = Z 0 перемещают в антиградиентном направленииж



