Тема 10. Оптимизация производства по экономическим критериям

10.1. Экономические показатели производства

Кинетическая модель химического процесса позволяет предсказать варианты решений по типу реакторов и параметрам процесса, наиболее выгодным с точки зре­ния удельной производительности и селективности. Однако при варьировании каких-либо условий процесса удельная производительность и селективность нередко изменяются в противоположных направлениях либо появляются дополнительные затраты на стадиях подготовки реакционной смеси или разделения продуктов. Например, снижение степени конверсии или применение избытка второго реагента часто благоприятствует росту селективности и удельной производительности, но сопровождается расходами на выделение и рециркуляцию непревращенных веществ; а повышение концентрации катализатора или инициатора увеличивает производительность, но связано с дополнительными материальными затратами. Повышение давления газофазных процессов, способствуя росту производительности, а часто и селективности, в то же время вызывает дополнительный рас­ход энергии на компримирование. Изменение температуры, бла­гоприятное для какого-либо из показателей процесса, может обусловить применение более дорогостоящих теплоносителей или конструкционных материалов и т. д. Поэтому оптимизация процесса по таким показателям, как максимум выхода или селективности по целевому продукту, высокая удельная произво­дительность, практически никогда не дает удовлетворительных результатов. Единственно надежными критериями являются эко­номические факторы.

Важным экономическим показателем производства является себестоимость целевого продукта, т.е. стоимость производства единицы продукции. Она складывается из четырех видов затрат: материальные затраты (сырье и материалы), энергетические затраты, затраты на оборудование, которые складываются из амортизационных отчислений и эксплуатационных расходов, заработная плата работающих и другие денежные расходы.

Главная статья себестоимости ‒ это материаль­ные затраты, основной причиной изменения которых является селективность, зависящая от работы реакционного узла. Сущест­венное влияние на снижение материальных затрат оказывает рецир­куляция непревращенных реагентов, а также ути­лизация побочных продуктов. Переход на синтез с использова­нием более дешевого сырья также снижает эту статью затрат.

Энергетические затраты представляют собой вторую по зна­чимости статью в себестоимости продукции. Они складываются из расхода тепловой и электрической энергии (работа насосов и компрессоров, нагревание и охлаждение по­токов, испарение жидких веществ, ректификация и др.). Важным элементом их экономии является систе­ма утилизации энергии.

Амортизационные отчисления, включаемые в себестоимость, служат источником для воспроизводства сооружений и обору­дования (ремонт, частичная или полная замена деталей и уз­лов).

Заработная плата работающих и другие денежные расходы за­висят от степени механизации и автоматизации производства, применения автоматизированных систем управления и т. д.

Минимум себестоимости ‒ это один из экономических критериев оптимальности производства.

Перечисленные выше затраты складываются из расходов на всех стадиях процесса, при чем каждый его узел вносит свой вклад в величину этих расходов. Если ограничиться (и в ряде случаев вполне реальной) задачей оптимизации от­дельных реакционного узла, то можно учитывать только переменные расходы по реак­ционному узлу и смежным стадиям, на которые непосредственно влияет варьирование условий процесса. Следовательно, в стоимость процесса входят переменные затраты, которые обозначают через 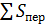. Они зависят от оптимизируемых параметров, например, стоимость реагентов, расход которых зависят от изменяемых параметров, энергетические затраты, стоимость теплоносителе и т.д. Затраты же по другим стадиям производства принимают условно постоянными и обозначают через 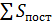. Затраты на рециклизацию непревращенного реагента ‒ через 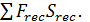Кроме того, необходимо учесть расходы по реакционному узлу S_R. Часть их (S_R,_V) пропорциональна объему реактора (стоимость оборудования и его ремонта), а остальные (S_R,₀) - постоянные во времени (контрольно-измерительные приборы, заработная плата обслуживающего персонала и т.д.). Часовая стоимость работы реакционного узла будет суммой

Кроме того, при реализации побочных продуктов их стоимость 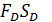вычитается из стоимости процесса.

Тогда часовая стоимость процесса составит:

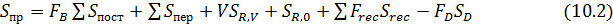
а себестоимость продукта В:

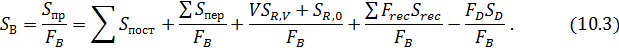
Принимая во внимание, что 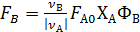, в уравнении (10.3) фигурируют такие показатели производства, как сте­пень конверсии, селективность, объем реактора. Выразив эти показатели количественно, можно найти минимум суммы пере­менных затрат и минимум себестоимости продукта.

10.2. Оптимизация реакционного узла по экономическим критериям

Влияние единичной мощности оборудования. Расходы на заработную плату, амортизационные отчисления и удельные капитальные вложения растут в дробной степени от величины потоков или объема оборудования. Это же относится к непроизводительным потерям сырья и продук­ции. Таким образом, при прочих равных условиях себестои­мость снижается при увеличении единичной мощности любого оборудования, в том числе и реактора.

Оптимизация концентрации гомогенного катализатора. Из­менение концентрации катализатора влияет на материальные затраты на катализа­тор (включая стадию его удаления из реакционной смеси) и интенсивность процесса, т.е. на затраты на оборудование. Если производительность установки задана, то для минимизации себестоимости достаточно минимизировать сумму 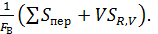При постоянстве других затрат другие слагаемые уравнения (10.3) оказываются постоянными, поэтому при оптими­зации достаточно противопоставить эти статьи расходов.

Пример 1. Гомогенно-каталитическая реакция А→В с кинетическим уравнением r =2000 С_КС_А кмоль·л^-1·ч^-1 проводится в РИС.

Найти оптимальную концентрацию гомогенного катализатора, если Х_А =0,99; 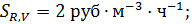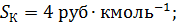C_A0 = 1 кмоль·л^-1.

Решение

В переменные затраты 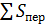входят только расходы на катализатор, которые составят

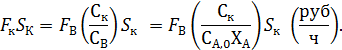
Объем реактора находят по характеристическому уравнению РИС:

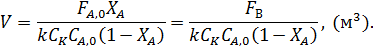
Следовательно, минимизации подлежит сумма:

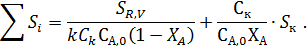
При заданных значениях F_В и Х_А для нахождения минимума берут производную и приравнивают ее к нулю

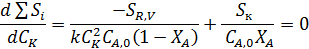
Оптимальная концентрация катализатора будет равна

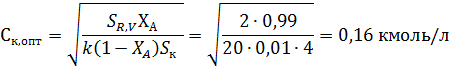
Из данного уравнения видно, что оптимальная кон­центрация катализатора тем больше, чем выше степень конверсии и затраты на реактор, пропорциональные его объему, а также чем ниже константа скоро­сти реакции и цена катализатора.

Пример 2. Найти для примера 1 по критерию себестоимости оптимальную концентрацию катализатора, если все условия остаются преж­ними, но F _Ви F _А,0 могут изменяться, C_A0 = 1 кмоль·л^-1; S_R,0 = 5 руб· ч^-1 и V =4 м³.

Решение

Минимизации подлежит сумма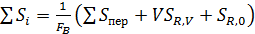

Из кинетики реакции находят

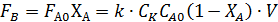
Так как 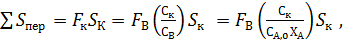то подлежащая минимизации сумма составит:

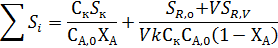
Берут производную и приравнивают ее к нулю:

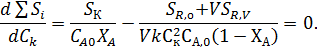
В результате получают:

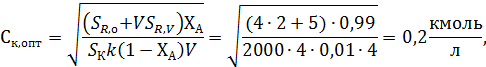
Следовательно, при данных условиях становится более выгодным повышение концентрации катализатора, т. е. некоторая интенсификация производства.

Оптимизация степени конверсии. Эта задача часто является одной из важнейших, поскольку степень конверсии сильно влияет на удельную производительность реакторов и на селективность. При оптимизации степени конверсии необходимо рассматривать вместе расходы по реакционному узлу и расходы на рециркуляцию (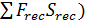, которые пропорциональны величине рециркулируемого потока.

Пример 3. Целевой продукт В получают по реакции второго порядка.

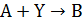
в изотермических условиях в РИС при следующих условиях:

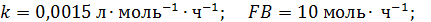
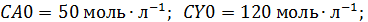
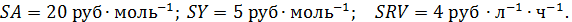
Найти оптимальную степень конверсии, себестоимость продукта В, объем реактора и начальные мольные потоки реагентов.

Решение.

Задачу решают в программе Mathcad.

Стоимость процесса составляет

.

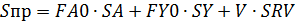Формулы для расчета:

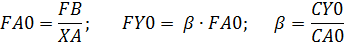
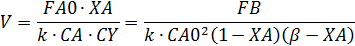
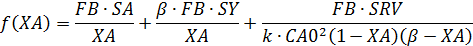
Given

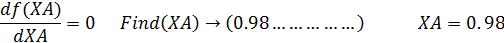
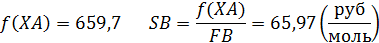
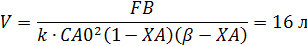
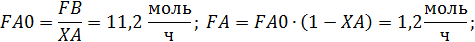
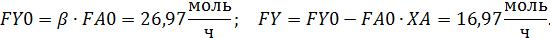
Пример 4. Целевой продукт В получают по реакции второго порядка

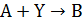
в изотермических условиях в РИС c рециклом непревращенного реагента А по схеме, представленной на рис. 10.1 Условия проведения процесса:

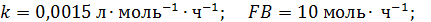
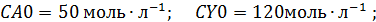
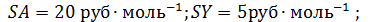
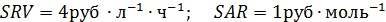
Найти оптимальную степень конверсии, себестоимость продукта В, объем реактора и начальные мольные потоки реагентов.

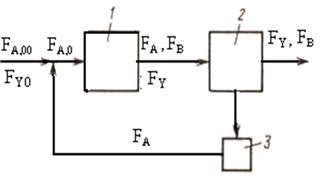
Рис. 10.1. Схема потоков при рециркуляции непревращенного реагента А: 1 – реакционный узел; 2 – блок отделения непревращенного реагента; 3 – блок рециркуляции

 

Решение

Задачу решают в программе Mathcad.

Стоимость процесса составляет:

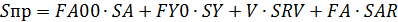
Формулы для расчета:

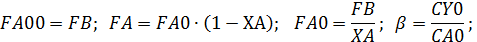
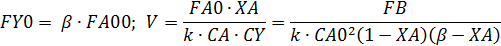
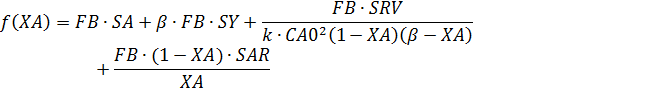
Given

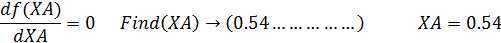
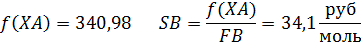
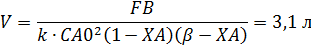
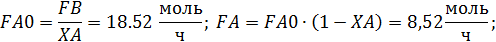
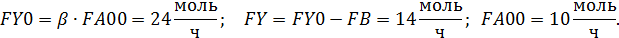
Пример 5. В РИС в изотермических условиях протекают параллельные реакции второго порядка:

Найти оптимальную степень конверсии, себестоимость продукта В, объем реактора РИС и начальные мольные потоки реагентов. При той же степени конверсии определить объем РИВ. Задачу решить в программе Mathcad.

Исходные данные:

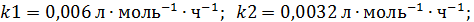
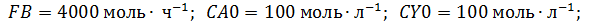
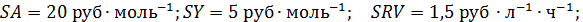
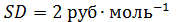
Решение

 

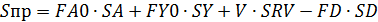
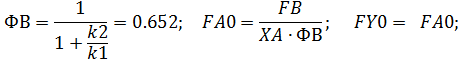
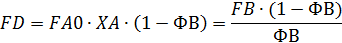
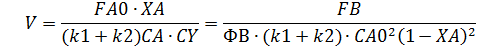
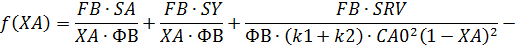
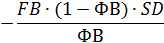
Given

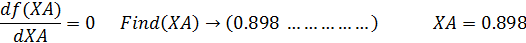
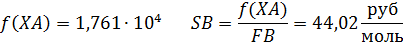
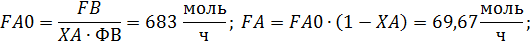
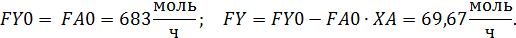
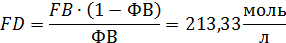
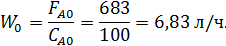
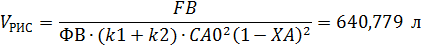
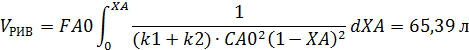
Пример 6.Целевой продукт В получают в РИС

в изотермических условиях c рециклом непревращенного реагента А по схеме, представленной на рис. 10.2.

Исходные данные:

 

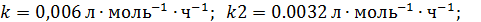
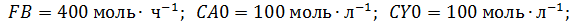
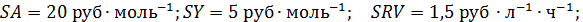
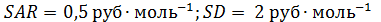
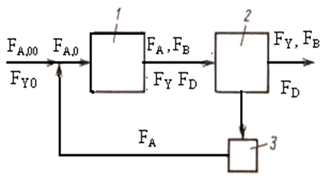
Рис. 10.2. Схема потоков при рециркуляции непревращенного реагента А, если целевой продукт В является промежуточным продуктом последовательной реакции: 1 – реакционный узел; 2 – блок отделения непревращенного реагента; 3 – блок рециркуляции

 

Решение

Задачу решают в программе Mathcad.

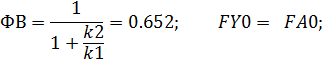
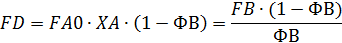
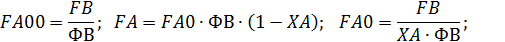
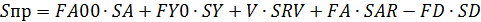
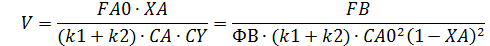
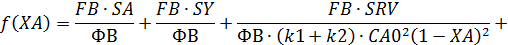
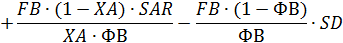
Given

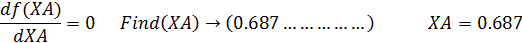
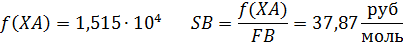
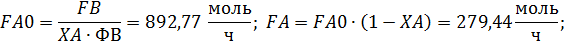
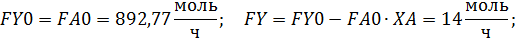
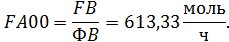
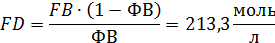
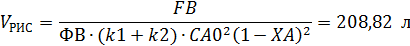
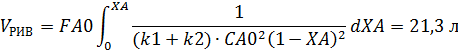
Пример 7. Целевой продукт В получают при последовательных реакции второго порядка в изотермических условиях в РИВ объемом V =1 м³:

c рециклом непревращенного реагента А по схеме, представленной на рис. 10.2.

Из экспериментальных данных известно, что k ₂/ k ₁ = 0,5. Цена реагента А равна S _А=20 руб·моль^-1; начальная концентрация С_A,0=2 моль·л^-1; затраты на выделение и рециркуляцию непревращенного реагента А S_{re c}= 3руб·моль^-1; S_{R ,0}=4 pyб; S_R,V = 2руб ·м^-3·ч^-1.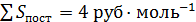

Найти оптимальную степень конверсии в условиях рециркуляции непревращенного реагента А, если: а) побочный продукт является бесполезным отходом; б) побочный продукт реализуют по цене 7 руб /кмоль.

Решение

Из уравнений материального баланса 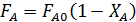, откуда

 

 

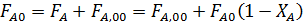
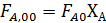
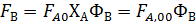
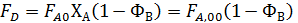
В соответствии с кинетикой процесса характеристическое уравнение РИВ имеет вид:

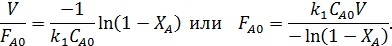
Интегральная селективность по промежуточному продукту В для последовательных реакций первого порядка в РИВ:

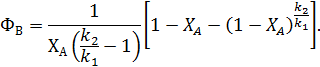
Часовая стоимость процесса:

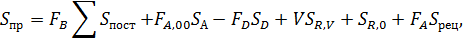
а себестоимость продукта В:

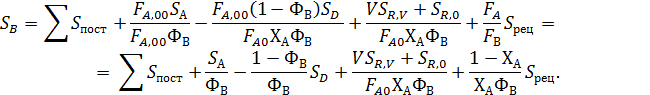
Подставляя выражение 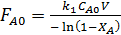, получают уравнение, связанное со всеми параметрами процесса.

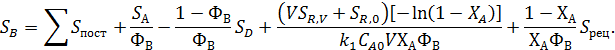
По нему при разной степени Х_А находят каждое слагаемое:

ХА	0,1	0,2	0,3	0,4	0,5	0,6	0,7
ФВ	0,97	0,94	0,91	0,87	0,83	0,78	0,71
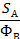
	20,6	21,3	22,0	23,0	24,1	25,7	28,2
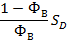
	0,22	0,45	0,69	1,05	1,44	1,98	2,86
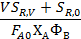
	1,9	2,0	2,2	2,6	2,9	3,4	4,2
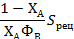
	27,8	12,8	7,7	5,2	3,6	2,6	1,8
SB
без реализации	54,3	40,1	36,9	34,8	34,6	35,7	38,2
с реализацией	54,08	39,65	36,21	33,75	33,16	33,72	35,34

Графическое изображение полученных данных представлено на рис. 10.3. Материальные затраты (кривая 1) растут с повышением степени конверсии в связи со снижением селективности, умень­шаясь при реализации побочных продуктов (кривая 1-1). Затраты на рециркуляцию (кривая 2) увеличиваются при снижении степени конверсии из-за роста рециркулируемого потока, а амортизацион­ные отчисления (кривая 3) растут с повышением степени конверсии в результате уменьшения удельной производительности уста­новки.

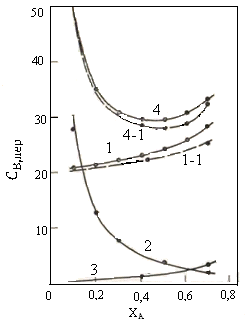
Рис. 10.3. Зависимость переменных слагаемых себестоимости от степени конверсии: 1 – материальные затраты без реализации побочного продукта; 1-1 - то же с реализацией побочного продукта; 2 - расходы, связанные с отделением и рециркуляцией непревращенного реагента; 3- амортизационные отчисления; 4 – сумма переменных затрат в себестоимости продукции без реализации побочного продукта, 4-1- то же с реализацией последнего.

Та­ким образом, сумма переменных слагаемых себестоимости име­ет минимум при определенных степенях конверсии (в рассмот­ренном примере при Х_А= 0,45 без утилизации побочного продук­та и при Х_А=0,50 с утилизацией). Оптимальная степень конверсии увеличивается, если рецикл непревращенного реагента отсутствует. В этом случае слагаемое себестои­мости S_А/Фв превращается в Sа/Ха·Фв и минимум себестоимости находится вблизи степени конверсии, соответствующей максимальном выходу целевого продукта η_В = Ха·Фв, в данном примере при Х_А=0,75.

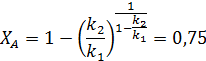
В приведенных в этом разделе примерах оптимизировался только один параметр при постоянстве остальных. В действи­тельности необходимо отыскивать глобальный минимум себестоимости, или удельных приведенных затрат, либо максимум прибыли, являющийся функцией множества параметров процесса. Такая многопараметрическая задача оптимизации выходит за рамки данного курса.

Вопросы для самопроверки

1. Назовите затраты, из которых складывается себестоимость продукции.

2. Расскажите об оптимизации производства по экономическим критериям.

3. Расскажите об оптимизации реакционного узла для проведения простых реакций без рецикла непревращенного реагента.

4. Расскажите об оптимизации реакционного узла для проведения сложных реакций без рецикла непревращенного реагента.

5. Расскажите об оптимизации реакционного узла для проведения простых реакций с рецикла непревращенного реагента.

Контрольные задачи

Приведены в Сборнике задач по курсу «Теория химико-технологических процессов органического синтеза» - Инженерные расчеты в химической технологии (работа 6).