Решение системы линейных уравнений

Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки А2:В3, а свободные члены – в ячейки D2:D3 (рис. 6.5).

Вспомним, что решение линейной системы АХ = В, где А – матрица коэффициентов, В – столбец (вектор) свободных членов, Х – столбец (вектор) неизвестных, имеет вид Х = А^-1В, где А^-1 – обратная матрица к А.

В нашем случае

.

Поэтому для решения системы уравнений

1. Выберите тот диапазон, в который будет введено решение. Например, F2:F3.

2. Введите в него формулу

=МУМНОЖ(МОБР(А2:В3);D2:D3)

3. Завершите вод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (рис. 6.5):

{=МУМНОЖ(МОБР(А2:В3);D2:D3)}

Рис. 6.5. Решение системы линейных уравнений

Таким образом, решением системы уравнений является вектор

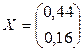
В качестве более сложного примера решим систему линейных уравнений

А²Х = В, где

.

Решение этой системы является вектор Х = (А²)^-1В.

Для нахождения вектора Х:

1. Введите элементы матрицы А в диапазон ячеек А2:В3.

2. Введите элементы вектора В в диапазон ячеек D2:D3.

3. Выберите диапазон F2:F3, куда поместим элементы вектора решения.

4. Введите в этот диапазон формулу:

=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)

5. Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива:

{=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)}

В диапазоне ячеек F2:F3 будет найдено решение системы уравнений

Нахождение значения квадратичной формы

Рассмотрим пример вычисления квадратичной формы 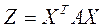, при этом

Для нахождения этой квадратичной формы:

1. Введем элементы матрицы A в диапазоне ячеек А2:В3 и вектора X в диапазоне ячеек D2:D3.

2. Выберем ячейку F2 для вычисления значения формы.

3. Введем формулу:

=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3); A2:B3);D2:D3)

4. Завершим ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (см. рис. 6.6):

{=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3); A2:B3);D2:D3)}

 

Рис. 6.6. Нахождение значения квадратичной формы

 

В ячейке F2 будет получено искомое значение формы 196.

 

Примеры использования матричных операций в экономических задачах

 

Пример 1. Данные о доходах (тыс. ден. ед.) холдинговой компании по трем регионам трех компаний за 2000 и 2002 гг. представлены в матрицах А и В:

Здесь элемент a_ijматрицы Аозначает доход i-й компании в j-м регионе за 2000 г. Аналогично – для матрицы В,но за 2002 г. Вычислите матрицу С приростов доходов за период с 2000 по 2002 г. и проанализируйте ее. Рассчитайте матрицу С_ср, характеризующую средние размеры приростов доходов компаний холдинга за год.

Решение.

1) Матрица С приростов доходов за рассматриваемый период равна:

С = В – А.

 

Элементы матрицы Свыражают изменение доходов с 2000 по 2002 г. Так, третья компания по первому региону потерпела убытки в размере 40 тыс. ден. ед. (c₃₁ = - 40), эта же компания (третья) по третьему региону в этот же период не принесла доходов (с₃₃ = 0).

2) Матрица С_ср, характеризующая средние размеры приростов доходов компаний холдинга за год, равна матрице С, деленной на n – количество лет в рассматриваемом периоде. В период с 2000 по 2002 г. входит 2 года (т.е. 2000 и 2001гг.), значит, n= 2, тогда: С_ср = C/2

 

Пример 2. Предприятие производит продукцию трех видов. При этом используется сырье трех типов. Нормы затрат сырья на единицу продукции каждого вида, себестоимость каждого вида сырья и стоимость его доставки приведены в таблице.

 

Показатель	Норма затрат сырья на единицу продукции, у. е.
I тип	II тип	III тип
Вид продукции
Себестоимость единицы сырья, ден. ед.
Стоимость доставки единицы сырья, ден. ед.

 

Каковы общие затраты предприятия на производство 100 у.е. продукции первого вида, 75 у.е. второго вида и 50 у.е. третьего вида?

 

Решение.

Нормы расходов сырья на единицу продукции запишем в виде матрицы А:

,

у которой элементы а_ij выражают количество сырья j-го типа на изготовление единицы изделия i-го вида. Пусть матрица С характеризует себестоимость единицы сырья и стоимость доставки единицы сырья:

Объем производства продукции задается матрицей-столбцом

Чтобы определить общие затраты S на производство продукции данного объема Q,надо знать затраты Рна сырье для производства единицы продукции каждого вида и его доставку. Для этого умножим матрицу расходов Ана матрицу С^т. Получим:

P = A · С^т

 

Тогда суммарные затраты составят S = Q^T * P:

 

 

 

Пример 3. Фабрика специализируется на выпуске изделий трех типов. При этом используется сырье трех видов: S_1, S₂, S₃. Нормы расхода каждого из них на единицу продукции каждого типа и объем расхода сырья на 1 день заданы таблицей:

 

Вид сырья	Нормы расхода на единицу продукции	Объем сырья на 1 день
1 тип	II тип	III тип
S1
S2
S3

 

Найдите ежедневный объем выпуска продукции каждого типа, учитывая, что сырье должно быть использовано полностью.

 

Решение.

Матрица нормы расхода имеет вид:

Матрица запаса сырья имеет вид:

Обозначим неизвестные объемы выпуска продукции через х_1, х₂ и х₃:

X= [х₁ х₂ х₃]^T. Тогда условие задачи можно записать в виде матричного уравнения АХ = В,откуда X =А^-1В, при условии, что А^-1 существует.

 

 

Пример 4. В таблице приведены расценки на выполнение работ для каждого вида оборудования.

 

Вид работ	Нормативы по видам оборудования, ден.ед.	Полные затраты на эксплуатацию, ден.ед.
механическое	тепловое	энергетическое
Тех. обслуживание
Текущие услуги
Капитальный ремонт

 

Найдите расчетные объемы работ (количество часов использования оборудования), которые смогут окупить затраты на эксплуатацию.

Решение.

Пусть необходимо х₁ч работы механического оборудования, х₂ чработы теплового оборудования и х₃ч работы энергетического оборудования, чтобы окупить затраты на техническое обслуживание, текущие услуги и капитальный ремонт. Тогда из условий задачи следует система уравнений:

3х₁ + х₂ + 4х₃ = 85

2х₁ + 2х₂ + 3х₃ = 82

10х₁ +20 х₂ + 15х₃ = 580

 

или в матричной форме АХ = В, где

 

 

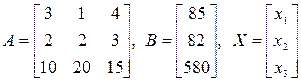
Чтобы окупить затраты на эксплуатацию, оборудование должно иметь следующий объем работ: механическое оборудование – 12 ч работы; тепловое – 17 ч; энергетическое – 8 ч.