Нахождение корней уравнения методом деления отрезка пополам

Хорошим упражнением по работе с Excel является программирование на рабочем листе алгоритма нахождения корня уравнения F(x)=0 методом деления отрезка пополам. Пусть непрерывная функция F(x) имеет значения разных знаков на концах отрезка [a;b], т.е.

F(a)F(b)<0.

Тогда уравнение F(x)=0 имеет корень внутри этого отрезка. Отрезок [a;b] называется отрезком локализации корня.

Пусть с=(a+b)/2 – середина отрезка [a;b]. Если F(a)F(c)£0, то корень находится на отрезке [a;c]; если F(a)F(c)>0, то за новый отрезок локализации берём [c;b].

Отметим, что новый отрезок локализации корня в два раза меньше первоначального. Процесс деления отрезка для локализации корня продолжаем до сих пор, пока его длина не станет меньше e, точности нахождения корня. В этом случае любая точка отрезка локализации отличается от корня не более чем на e/2.

На рис. 4.3 приведены результаты нахождения корня с точностью до 0,001 методом деления отрезка пополам уравнения х² – 2 = 0. За первоначальный отрезок локализации корня выбран [0;2].

 

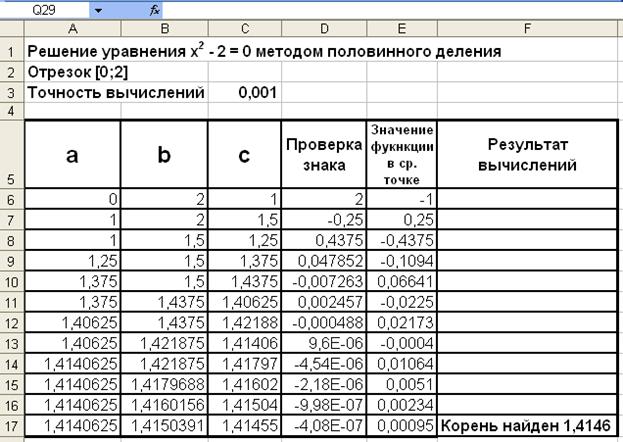
Рис. 4.3. Нахождение корня уравнения методом деления отрезка пополам

 

Для реализации этого метода необходимо ввести в ячейки рабочего листа формулы либо значения, приведенные в табл. 4.1.

 

Таблица 4.1 – Формулы для нахождения корней уравнения

Ячейка	Формула либо значение
A6
B6
C6	=(A6 + B6)/2
D6	=(A6^2 – 2)*(C6^2 – 2)
E6	=C6^2 – 2
F6	=ЕСЛИ(В6 – А6<$C$3; “Корень найден и равен” &Текст(С6; “0,0000”); ““)
A7	=ЕСЛИ(D6<=0;A6;C6)
B7	=ЕСЛИ(D6<=0;C6;B6)
C7	=(A7+B7)/2
D7	=(A7^2-2)*(C7^2 – 2)
E7	=C7^2 – 2
F7	=ЕСЛИ(В7 – А7<$C$3; “Корень найден и равен” &ТЕКСТ(С7; “0,0000”);””)

Замечание. Функция ТЕКСТ – это функция из категории функций по работе с текстом. Она преобразует значение в текст в заданном числовом формате:

ТЕКСТ (значение; формат)

- значение – это числовое значение или ссылка на ячейку;

- формат – это числовой формат с вкладки Число диалогового окна Формат ячеек.

Далее следует выделить диапазон ячеек А7:F7 и с помощью маркера автозаполнения протащить его вниз до тех пор, пока в столбце F не появится сообщение о том, что корень уравнения найден.

 

Примеры выполнения заданий

 

Построить графики функции y = x², используя внедренные диаграммы типа "График" и "Точечная диаграмма". Результаты сравнить.

Порядок выполнения задания:

· Составить таблицу значений функции:

Значение аргумента	Значение функции
-6
-5
-4
-3
-2
-1

· Выделить второй столбец таблицы.

· Вызвать Мастер диаграмм.

· В первом диалоговом окне выбрать тип диаграммы График, подтип График с маркерами, помечающими точки данных.

· Во втором диалоговом окне включить опцию Ряды в столбцах. На вкладке Ряд в качестве подписи меток по оси категорий задать значения первого столбца данных, выделив их в таблице.

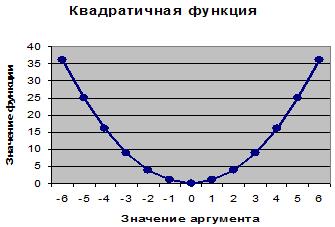
· На третьем шаге работы Мастера диаграмм ввести название диаграммы "Квадратичная функция", ввести название оси категорий "Значение аргумента", ввести название оси значений "Значение функции".

· На четвертом шаге задать способ помещения диаграммы на листе, выбрав опцию имеющемся.

· Щелкнуть по кнопке Готово.

График будет иметь следующий вид:

 

· Вновь выделить второй столбец таблицы.

· Вызвать Мастер диаграмм.

· В первом диалоговом окне выбрать тип диаграммы Точечная диаграмма, подтип Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров.

· Во втором диалоговом окне включить опцию Ряды в столбцах. На вкладке Ряд в качестве подписи меток по оси категорий задать значения первого столбца данных, выделив их в таблице.

· На третьем шаге работы Мастера диаграмм ввести название диаграммы "Функция x^2", ввести название оси категорий "Значение аргумента", ввести название оси значений "Значение функции".

· На четвертом шаге задать способ помещения диаграммы на листе, выбрав опцию имеющемся.

· Щелкнуть по кнопке Готово.

График будет иметь следующий вид: