Истинная длина отрезка по частям пространства

Работая в ортогональных проекциях, следует действовать так:

8.2.1 Построить отрезок прямой в трех (или в двух) проекциях (см. Алгоритм 5.1).

8.2.2 Определить следы прямой (Алгоритм 7.1).

8.2.3 Построить истинную длину отрезка прямой, в соответствии с Алгоритмом 6.1.1 или 6.1.2, или отметить ее на одной из проекций, если прямая занимает частное положение (Алгоритм 6.1.3).

8.2.4 Проекция прямой, на которой выполнялись построения истинной длины, служит для отрезка истинной длины базовой линией разбиения, как в Алгоритме 8.1 для пропорционального деления отрезка. Направлением переноса служит перпендикуляр к этой проекции. Для разбиения истинной длины отрезка по частям пространства необходимо перенести проекции следов прямой с базовой проекции отрезка на отрезок истинной длины параллельно направлению переноса. Построенные на истинной длине следы служат точками перехода прямой из одного октанта в другой.

8.2.5 Определить положение в пространстве одной из крайних точек отрезка (см. Алгоритм 1.1). В найденном октанте отрезок будет лежать от крайней точки до ближайшего следа прямой.

8.2.6 Определить, в какую часть пространства переходит прямая. Если Вы затрудняетесь с определением октанта, можно вначале выяснить, как изменяются знаки координат точек на прямой после пересечения с плоскостью проекций. Изменение знака касается только той координаты, которая отсутствует в плоскости, содержащей данный след прямой

(таблица 10). Зная знаки координат точек на следующем участке прямой, Вы

8.2.7 определите октант для очередного ее отрезка от одного следа до другого.

8.2.8 Повторять действия, описанные в пп. 8.2.6 и 8.2.7, пока не достигнете второй крайней точки отрезка.

Таблица 10 – Изменение координат точек на прямой после пересечения с плоскостью проекций

След прямой	M	N	P
содержится в плоскости проекций	1	2	3
и после прохождения через нее изменяется знак следующей координаты:	z	y	x

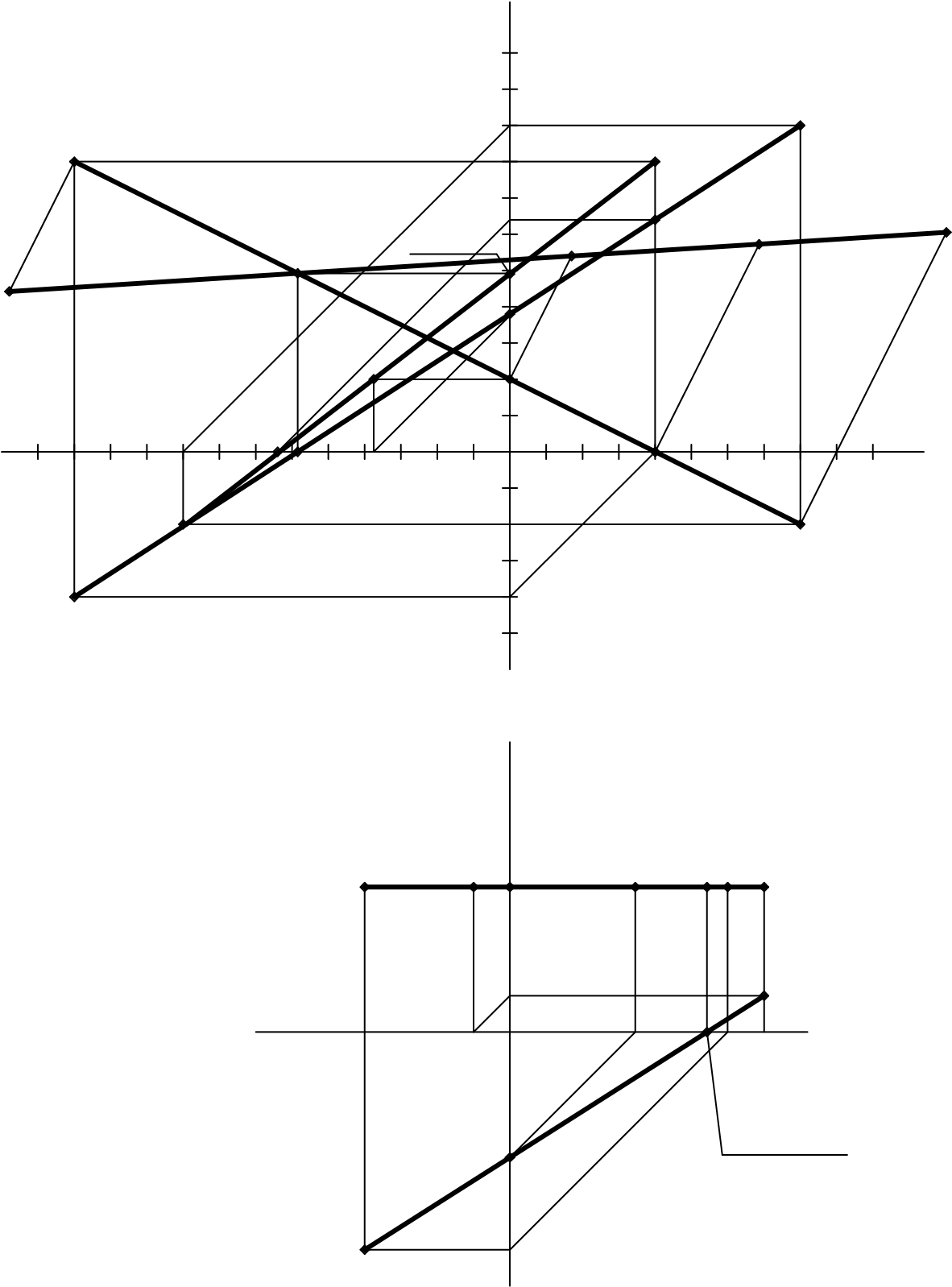
Рисунок 18 приводит пример реализации Алгоритма 8.2 для тех же отрезков прямых, что были построены на рисунках 7, а и 11, а.

z

I I B I A I I I

A

I I I

y A I N I, I N * I I N _I P * M V I I M * V I I B *

A * I I I P I I ^y _B

P _P

I I I I I

M M

x I I I N ^I O B I I y _B

I

A

y а) z

I I B I I I N I I, I P I I PI I I N I I A I I I B I I

A

I

B, B *

x O V I y

I

I N, N *

P, P * V

I I

A, A *

y а)

Рисунок 18 - Определение истинной длины отрезка прямой по частям пространства: а) для прямой общего положения; б) для прямой частного положения

Прямая АВ на рисунке 18, а была задана аналитическим способом. На основании координат концов отрезка были построены три его проекции (см. пояснение к рисунку 7, а). Прямая занимает общее положение, поэтому, в точках пересечений проекций прямой с осями координат, были построены проекции трех следов (см. пояснение к рисунку 14, а). Истинная величина отрезка АВ была определена методом трапеций (см. пояснение к рисунку 9, а). Отметим, что найденная истинная величина пересекает базовую проекцию A’’В’’ в точке одноименной проекции одноименного следа N’’ – за счет этого можно проверить точность построений методом трапеций.

Положение фронтального следа прямой на отрезке истинной длины совпадает с его проекцией: N*=N’’. Два оставшихся следа переносим с базовой, фронтальной проекции, вычертив связи, параллельные направлению переноса (A’’A* или В’’B*). Находим P* и M*.

Определяем последовательность прохождения прямой по частям пространства. Точка А лежит в I октанте (все три координаты положительны). При пересечении фронтальной плоскости проекций (точка N) прямая переходит во II октант. Очередная точка смены октанта – профильный след (точка P): следующий отрезок прямой (P*M*) находится в VI октанте. За горизонтальным следом (точка M) прямая окажется в VII части пространства. Проверяем координаты точки В – все они отрицательные, это характерно для VII октанта.

На рисунке 18, б выполнены построения для отрезка прямой АВ частного положения. Действия при этом, в целом, аналогичны уже описанным. Отличие состоит в том, что прямая параллельна плоскости ₁, поэтому истинная величина отрезка равна его горизонтальной проекции (A*B*=A’B’). Поэтому разбиение отрезка прямой по частям пространства выполнено именно на этой проекции: P’=P*, N’=N*.

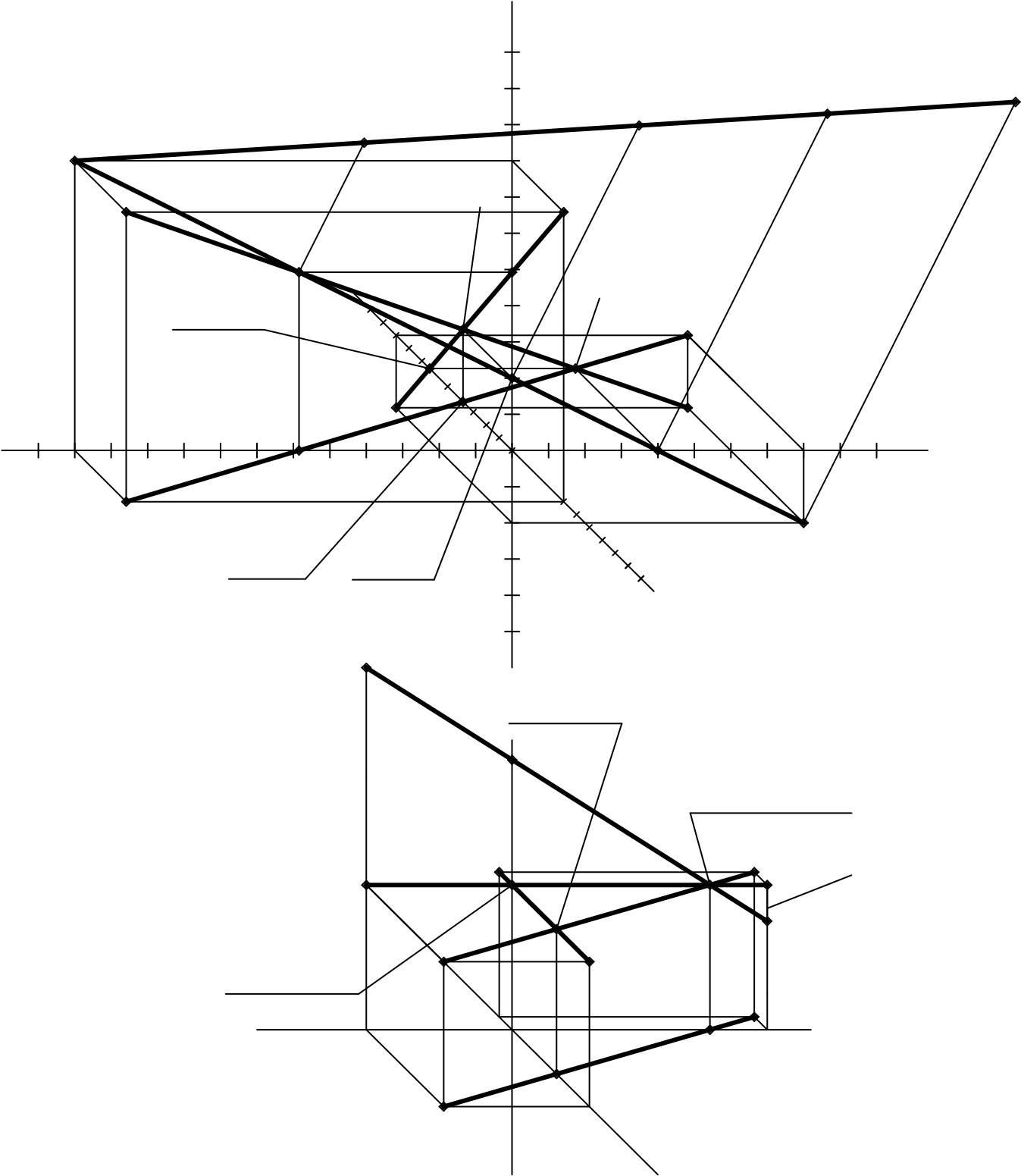
Во фронтальной косоугольной диметрии построения выполняются по той же схеме, т.е.: Алгоритм 5.2; Алгоритм 7.2; Алгоритм 6.2, а затем действия, описанные в пп. 8.2.4 – 8.2.7 (рисунок 19).

z

A I, I A * I N * I I I I I I I I P * V I M * V I I B *

P, P A

A N I, I N I I I I

I I I

M N M, M B I

I B I I I w ' B

N

x O M I I I I

I I I I B

A P P

y

A * I I I а)

_I P, P

y _A P * ^z V N ^I , ^I N, N *

A I I B I I I B B I I y B

P I, I N I I I A A I I I V B I I B *

x O N I

I

I P

A б) y

 

Рисунок 19 - Истинная длина отрезка прямой с разбиением по частям пространства в косоугольной фронтальной диметрии - для тех же прямых, что на рисунке 18

Прямая АВ на рисунке 19, а занимает общее положение. Построение следов в аксонометрии описано в пояснениях к рисунку 16, а. Истинная величина отрезка методом треугольника построена аналогично построениям, показанным на рисунке 13, б.

Перенос следов на отрезок истинной величины выполняется с базовой, фронтальной проекции

(A’’В’’). Направление переноса задает отрезок В’’B*, перпендикулярный A’’В’’. Параллельно ему строим N’’N*, P’’P* и M’’M*. Определение прохождения прямой по частям пространства было описано выше, в пояснении к рисунку 18, а.

Прямая АВ на рисунке 19, б находится в частном положении: она параллельна горизонтальной плоскости. В косоугольной фронтальной диметрии ее горизонтальная проекция искажена. Следовательно, истинная величина отрезка должна быть построена общим способом, на основе фронтальной проекции прямой.

Выполняем построение методом трапеций. Под прямым углом к A’’В’’ откладываем ординаты концов отрезка с учетом коэффициента искажения по оси OY в противоположных направлениях (y_A и y_B имеют противоположные знаки). Параллельно A’’A* или В’’B* строим связь P’’P*. Точка N* совпадает с N’’.

Точка В находится в VI октанте: координаты x_B и y_B отрицательны, а z_B - положительна. Проходя через фронтальную плоскость проекций (точка N), прямая переходит в V октант. За точкой P прямая будет лежать в I октанте. Проверим: у точки А все координаты положительны, это соответствует I октанту.

Рисунок 20 приводит пример оформления Задачи № 2 из альбома домашних заданий.

Построение следов плоскости

Как известно, плоскость, в общем случае, задается тремя точками, не принадлежащими одной прямой. Точки эти могут быть заданы аналитически или графически, занимать общее или частное положение, быть отдельно стоящими или принадлежать некоторым отрезкам прямых линий. Все эти возможности порождают разнообразие способов задания плоскости. Среди них особое место занимает определение положения плоскости ее следами, т.е. линиями пересечения этой плоскости с плоскостями проекций.

Умение переходить от одного способа задания плоскости к другому играет очень важную роль при решении позиционных и метрических задач.

Задание координат плоскости

Задание плоскости с помощью координат – это тот же способ задания с помощью трех точек, только точки эти занимают частное положение: каждая из них принадлежит одной из координатных осей. Таким образом, у каждой из них всего одна координата, отличная от нуля, что позволяет записывать положение плоскости аналитически в виде α (x_α; y_α; z_α), по аналогии с координатами точек.

Если координаты плоскости, или точки схода следов, заданы аналитически, то следы можно вычертить по следующему алгоритму (обозначения даны для плоскости ):

9.1.1 Обозначить точки схода следов на осях координат точно так же, как это делается для проекций точек на оси (см. Алгоритм 1). Если координата плоскости по некоторой оси равна бесконечности, то соответствующая точка схода следов не обозначается – это характерно для плоскостей частного положения. Информация о координатах плоскостей частного положения представлена в Таблице 11.

Таблица 11 - Координаты плоскостей частного положения

Координата			Плоскость
п	ерпендикуляр	на		параллельна
1	2	3	1	2	3
x	+/-	+/-		+/-		
y	+/-		+/-		+/-	
z		+/-	+/-			+/-

 

 

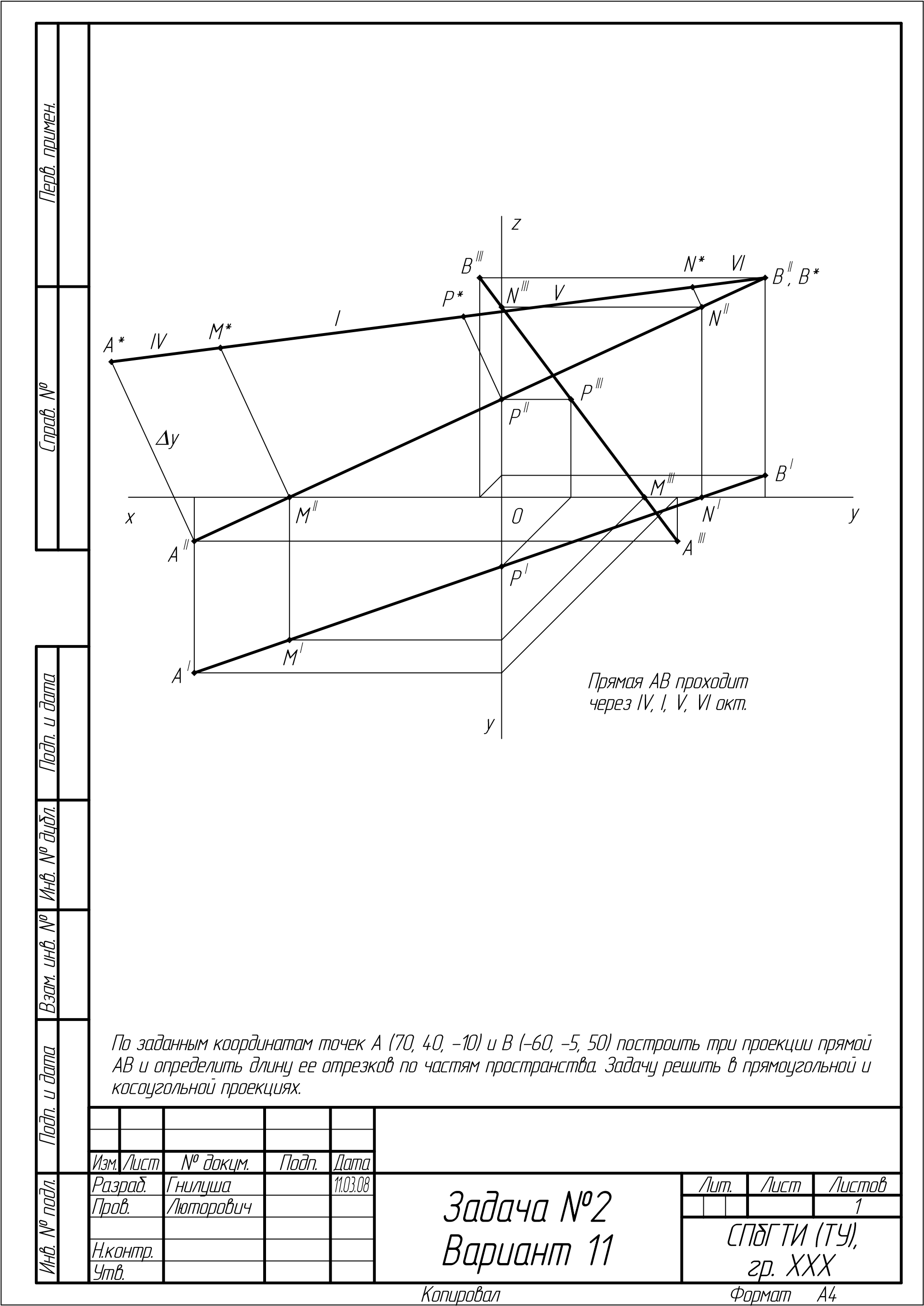
Рисунок 20 - Пример оформления задания, решенного по Алгоритмам 5 – 8

 

9.1.2 Соединить отрезками прямых линий точки, принадлежащие одной и той же плоскости проекций: точки X_α и Y_α определяют горизонтальный след плоскости h’_0; X_α и Z_α – фронтальный, f’’_0, и, наконец, Z_α и Y_α на оси y профильной плоскости проекций – профильный след p’’’_0. (Такие обозначения следов связаны с тем, что они представляют собой проекции прямых частного положения, лежащих в плоскости, см. Алгоритм 10). При прочерчивании следов нужно учесть тип линии: основной сплошной линией след прочерчивается только в том случае, если обе соединяемые координаты имеют положительное значение. В противном случае точки схода следов соединяют штриховой линией.

9.1.3 Если одна из координат плоскости, определяющих след, равна бесконечности, то такой след проводится от имеющейся точки схода следов параллельно той оси проекций, значение координаты для которой бесконечно. Если равны бесконечности обе координаты для некоторого следа, это значит, что плоскость параллельна данной плоскости проекций и, следовательно, следа на ней не образует.

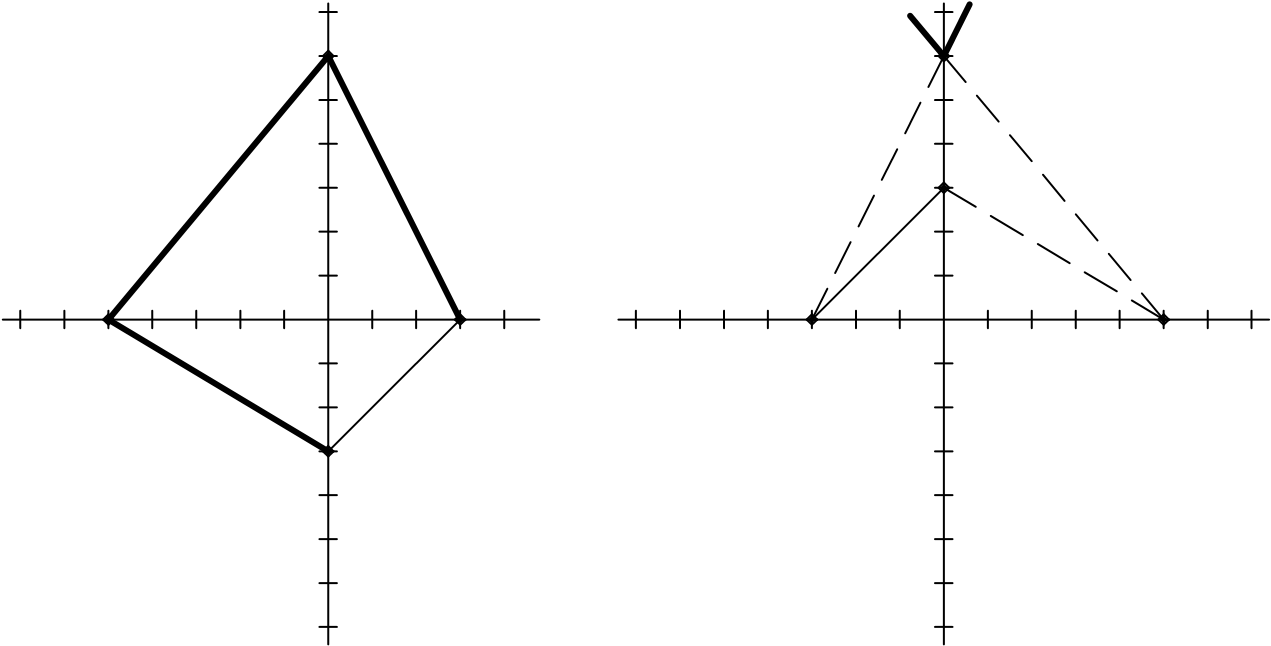
Построение следов для плоскостей, имеющих различные координаты, проиллюстрировано на рисунке 25.

(25; 15; 30) ^z (-2 5; -1 5; 30) ^z I I I ⁽; 15; 30) ^z

Z  p Z 

I I I I I

f 0 p 0 p 0_{} I I I

x X _{} O Y y x O Y _{}y

I

h _{0} Y  Y 

y а) y в)

Z  0 f 0 I I

I I Y f 0_{}

I

h 0_{}

Y _{}O X _{}y x

I

h 0_{}

y б)

 

Рисунок 21 - Построение следов плоскости, заданной координатами: а) плоскость общего положения с положительными координатами; б) плоскость общего положения с координатами разного знака; в) плоскость частного положения (профильно-проецирующая)