

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Самостоятельная работа № 15.
История развития и становления тригонометрии
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: подготовить реферат по предложенной теме.
Реферат должен быть выполнен с соблюдением методических рекомендаций по написанию реферата.
Самостоятельная работа № 16.
Преобразование тригонометрических выражений
Цель: Знать методы решения задач при помощи основных тригонометрических формул, уметь применять их при решении соответствующих заданий.
Методические рекомендации
Используя методические рекомендации, решите примеры:
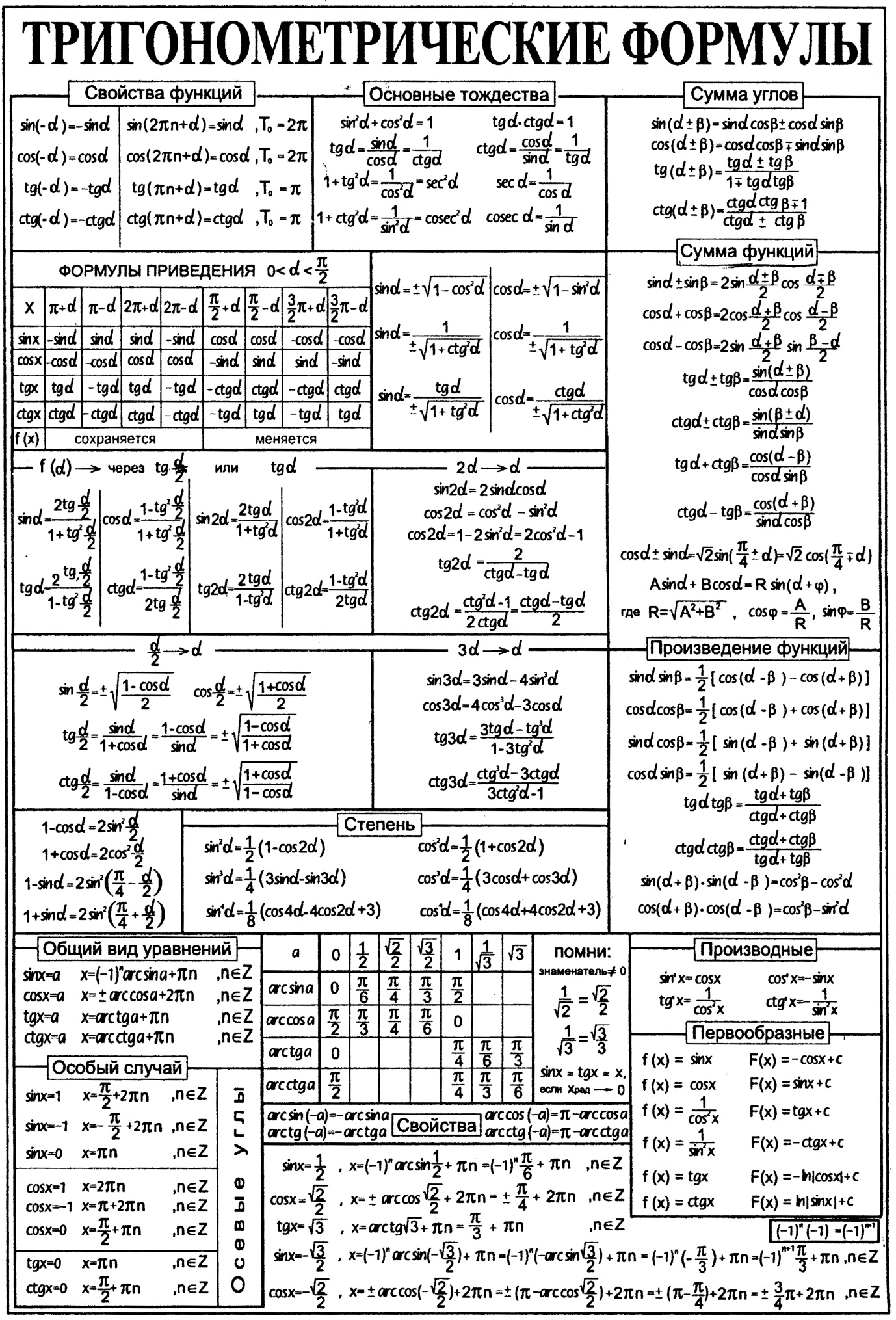
1) Основное тригонометрическое тождество. Найти:
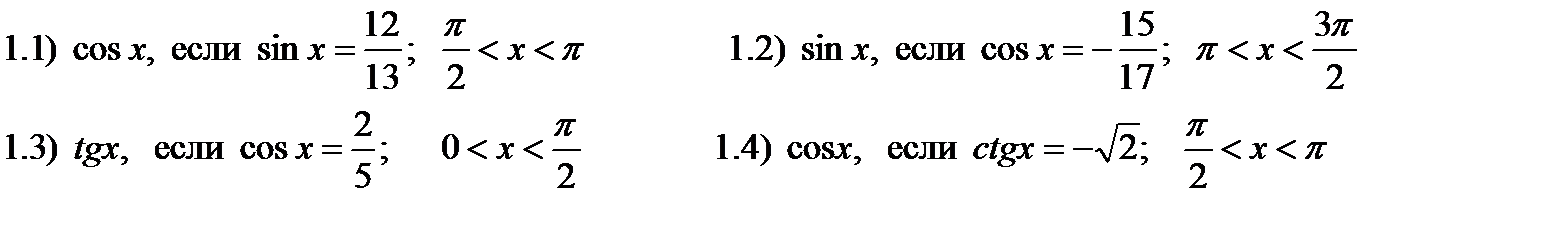
2) Формулы приведения, формулы сложения и двойного угла. Упростить:
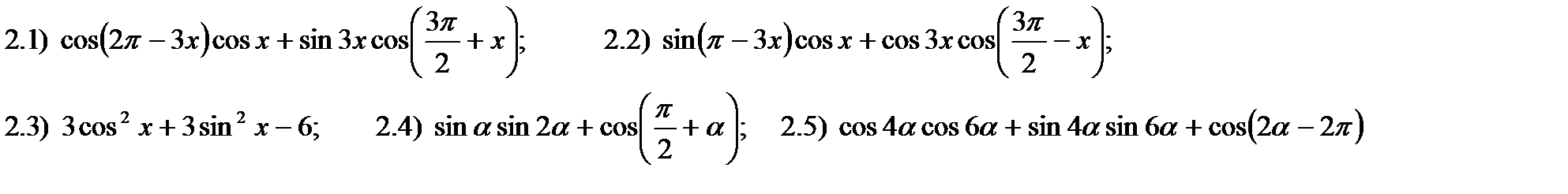
3) Найти значение выражения: 3.1) sin(p/2 + a) – 4cos(p-a), если cosa = -0,4;
3.2) 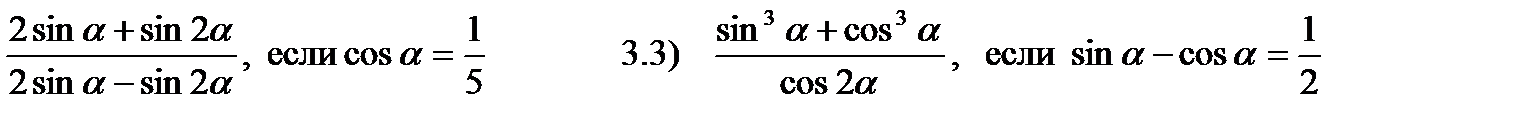
4) Вычислить:
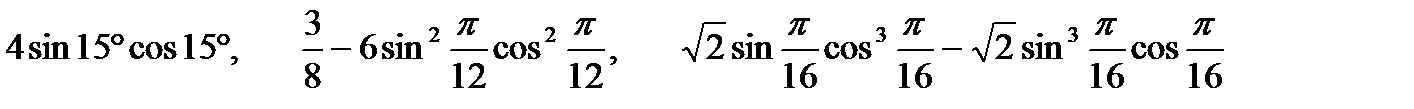 ,
, 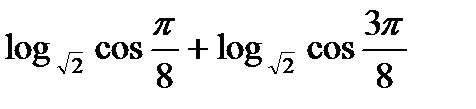
5) Доказать тождества:1) 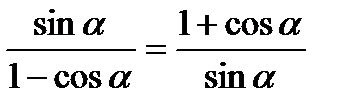 ; 2)
; 2) 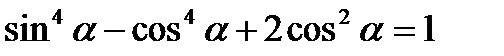 ; 3)
; 3) 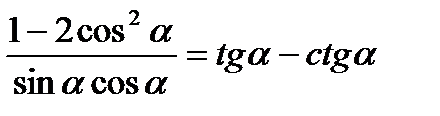
Самостоятельная работа № 17.
Решение тригонометрических уравнений повышенной сложности
Цель: Знать методы решения тригонометрических уравнений, формулы для нахождения корней, уметь использовать полученные знания при решении уравнений повышенной сложности.
Методические рекомендации
I. Решение простейших тригонометрических уравнений.
| Уравнение | Формулы решения | Частные случаи |
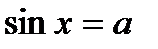
| при 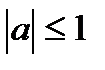 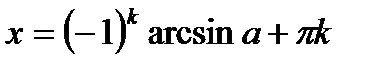 , , 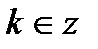 при
при 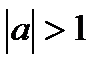 - решений нет - решений нет
| 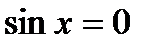 ; ; 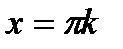 , , 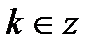
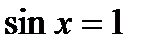 ; ; 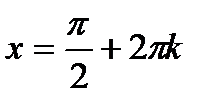 , , 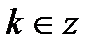
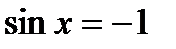 , , 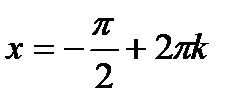 , , 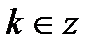
|
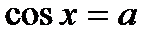
| при 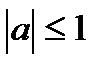 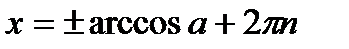 , , 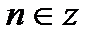 при
при 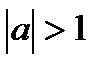 - решений нет - решений нет
| 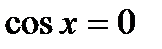 ; ; 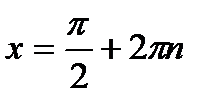 , , 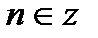
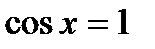 ; ; 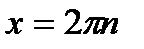 , , 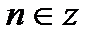
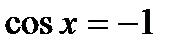 ; ; 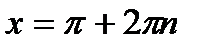 , , 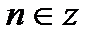
|
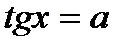
| 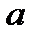 - любое число - любое число 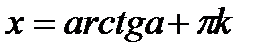 , , 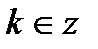
| - |
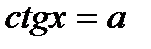
| 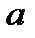 - любое число - любое число 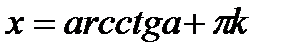 , , 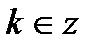
| - |
II. Тригонометрические уравнения.
| Уравнение | Способ решения | Формулы |
1. Уравнение содержит только синусы или косинусы (синусы и косинусы) вида
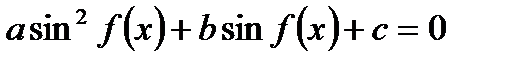
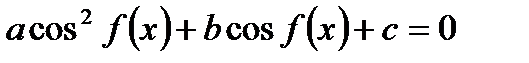 и т.д.
и т.д.
| Уравнение сводится к квадратному (биквадратному) относительно синуса (косинуса) | 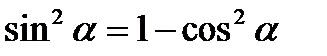
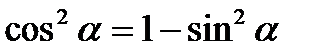
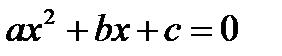
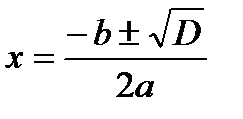
|
2. Однородное уравнение I степени вида
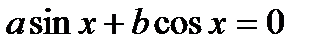
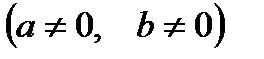
| Деление обеих частей на 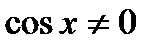 . Получаем: . Получаем: 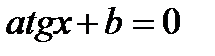
| 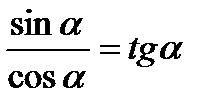
|
3. Однородное уравнение II степени вида
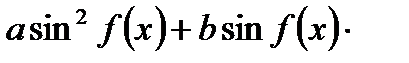
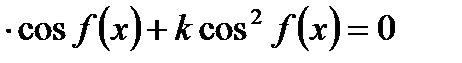
| Деление обеих частей на 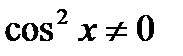 . Получаем: . Получаем: 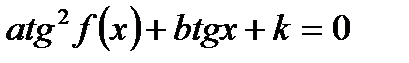
| 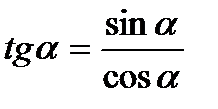
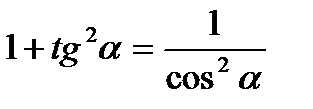
|
4. Уравнение вида
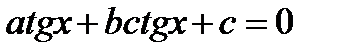
| Уравнение сводится к квадратному относительно тангенса заменой
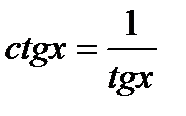
| 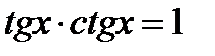
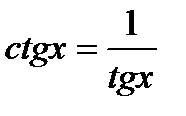
|
III. Основные тригонометрические тождества.
1. 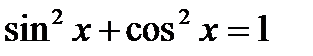 ;
; 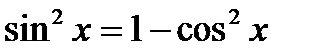 ;
; 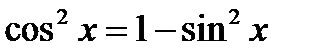
2. 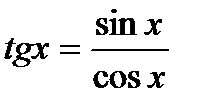
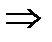
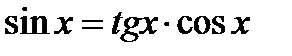
3. 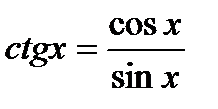
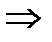
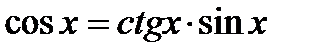
4. 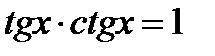
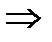
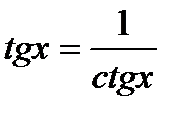 и
и 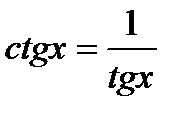
5. 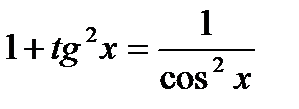
6. 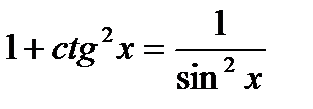
IV. Формулы сложения.
1. 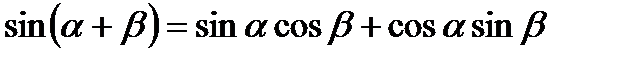
2. 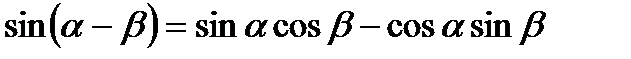
3. 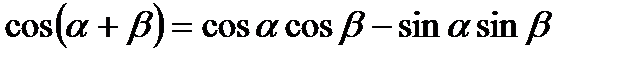
4. 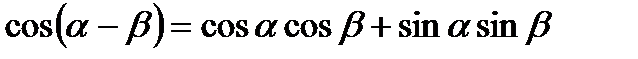
5. 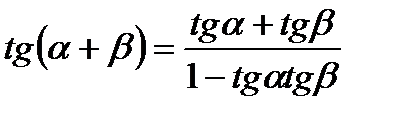
6. 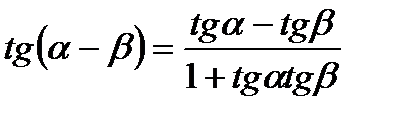
V. Формулы двойного и половинного аргументов.
1. 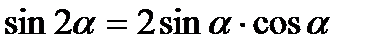
2. 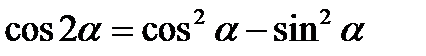 ;
; 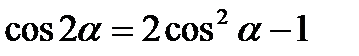 ;
; 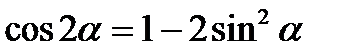
3. 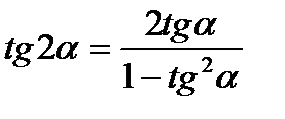
4. 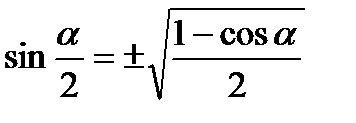
5. 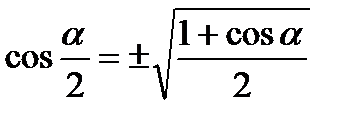
6. 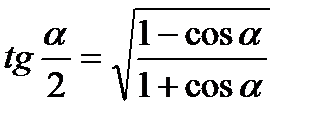
VI. Формулы суммы и разности одноименных тригонометрических функций.
1. 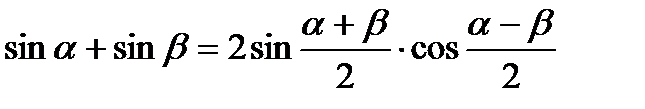
2. 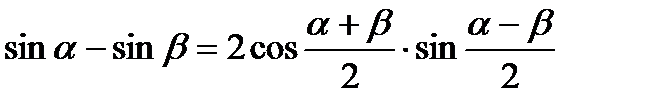
3. 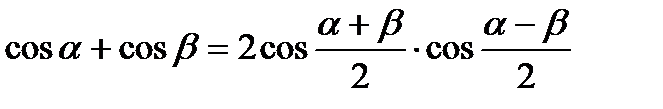
4. 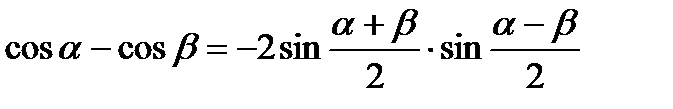
5. 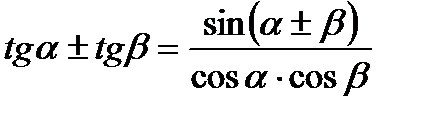
Значения тригонометрических функций
| град | |||||
| радиан | 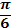
| 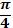
| 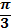
| 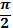
| |
sin 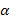
| 
| 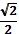
| 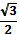
| ||
cos 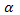
| 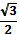
| 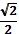
| 
| ||
tg 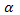
| 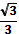
| 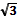
| не существ | ||
ctg 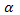
| Не существ | 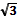
| 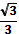
|
Используя методические рекомендации, решите уравнения:
1. 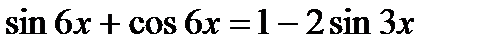 ;
;
2. 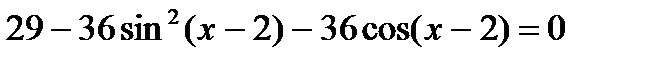 ;
;
3. 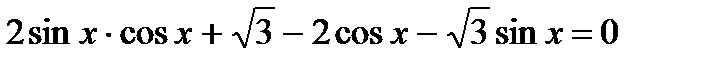 ;
;
4. 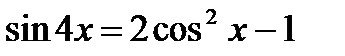 ;
;
5. 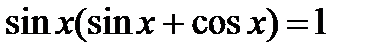 ;
;
6. 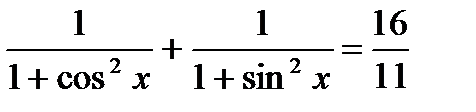 .
.
Подсказки.
1. Воспользуйтесь формулой двойного угла для 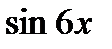 и
и 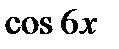 .
.
2. Обозначьте 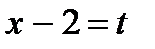 , решите уравнение, сведя его к квадратному с помощью формулы
, решите уравнение, сведя его к квадратному с помощью формулы 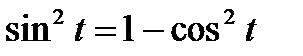 .
.
3. Сгруппируйте 1-ое и 3-е слагаемые, примените разложение на множители.
4. Воспользуйтесь формулой двойного угла для 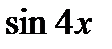 и
и 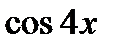 , формулой понижения степени
, формулой понижения степени 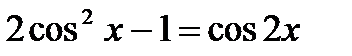 .
.
5. Раскройте скобки, примените основное тригонометрическое тождество.
6. Приведите дроби к общему знаменателю, а затем используйте основное тригонометрическое тождество 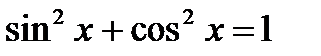 , сведите уравнение к квадратному.
, сведите уравнение к квадратному.
Раздел 7. Функции, их свойства и графики
Самостоятельная работа № 18.
|
|
|

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!