Поиск решений по имитационным моделям осуществляется осуществляется с помощью методов экспериментальной оптимизации на ЭВМ, являющихся особой разновидностью численных методов оптимизации. При этом разработчик модели сталкивается с необходимостью разработки не только собственно имитационного алгоритма, но и с разработкой специфических именно для этого алгоритма вспомогательных элементов – моделей входов, выхода, обратной связи (рис. 4.1.).
Следует отметить, что в программном обеспечении одновременных ЭВМ присутствуют пакеты прикладных программ (в первую очередь по разделу «Математическая статистика»), которые можно использовать при разработке тех или иных вспомогательных элементов конкретной имитационной модели. В связи с этим остановимся более подробно на задачах, ими решаемых.
Модели случайных входов
Создавая стохастическую имитационную модель, всегда приходится решать, следует ли в модели использовать имеющиеся эмпирические значения входных стохастических факторов непосредственно или целесообразно использовать их теоретико-вероятностные или частотные распределения. Непосредственное использование имеющихся статистических данных предполагает запись в память ЭВМ и выборку их из памяти определенным образом, обеспечивающим «чистоту» статистического эксперимента. В общем случае применение теоретических частотных или вероятностных распределений с учетом требований к машинному времени и памяти более эффективно, чем использование табличных данных для получения значений случайных факторов, необходимых в работе с моделью. Кроме того, использование необработанных эмпирических данных означает, что имитируется только прошлое. Возможными будут считаться только те события, которые уже происходили.
В связи с этим на практике в большинстве случаев эмпирические данные обрабатываются для получения наиболее близкого к ним теоретического закона распределения данной случайной величины и дальнейшего воспроизведения этого закона в процессе моделирования.
Для введения в моделирующий алгоритм случайных факторов используются специальные модели имитации случайных величин и событий. Эти модели являются основополагающими в статистическом моделировании, так как практически все остальные действия сводятся к преобразованию полученных случайных чисел по соответствующим правилам. В качестве исходной последовательности для получения случайных чисел с любым законом распределения либо для моделирования случайных событий используются случайные числа, равномерно распределенные в интервале (0 – 1). Наиболее распространенным способом получения таких чисел является программный. К настоящему времени создано большое количество разнообразных программ получения случайных чисел. В программное обеспечение современных ЭВМ входят стандартные программы генерирования случайных чисел, равномерно распределенных в интервале (0 – 1).
Преобразование случайных чисел с равномерным законом распределения в случайные числа с заданным (в общем случае произвольным) законом распределения базируется на теореме: если случайная величина yi имеет плотность распределения f(y), то случайная величина
 (4.1)
(4.1)
является равномерно распределенной в интервале (0-1).
Решение уравнения (4.1) относительно yi дает возможность получить искомое случайное число (рис. 4.2).

Рис. 4.2. Получение случайных чисел решением интегрального уравнения
Точное решение интегрального уравнения (4.1) возможно только для ряда относительно простых законов распределения, например:
1. Равномерное распределение с параметрами  и
и  :
:
 ;
;
 .
.
2. Показательное распределение с параметрами  :
:
 .
.
Но так как случайная величина (1- xi) также имеет равномерное распределение в интервале (1 – 0), справедливо
 .
.
Однако в большинстве практически важных случаях уравнение (4.1) относительно yi точно не решается, поэтому на практике большое развитие получили приближенные методы.
Метод преобразования равномерно распределенных случайных
чисел, базирующихся на центральной предельной теореме
теории вероятности
Для получения случайных чисел, распределенных по нормальному закону, можно воспользоваться центральной теоремой теории вероятности, согласно которой сумма большого числа случайных чисел, имеющих равномерное распределение в интервале (0-1), дает распределение, асимптотически приближающееся к нормальному. Поэтому для получения нормального распределения следует суммировать случайные числа, равномерно распределенные в интервале (0-1), при этом математическое ожидание М и среднеквадратическое отклонение  получаемого закона при достаточно большом числе случайных n будут определяться следующими выражениями:
получаемого закона при достаточно большом числе случайных n будут определяться следующими выражениями:

При n = 8 – 12 приближение к нормальному закону достаточно высокое для потребностей практики. Если необходимо смоделировать нормальный закон с параметрами математического ожидания  и среднеквадратического отклонения
и среднеквадратического отклонения 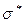 , то требуемые случайные числа yk получаются по формуле
, то требуемые случайные числа yk получаются по формуле
 ,
,
где k – номер случайного числа с заданным нормальным законом распределения.
Методы преобразования равномерно распределенных чисел,
базирующихся на аппроксимации экспериментальных законов
распределения
Пусть на основе экспериментального частотного распределения (рис. 4.3, а) построена экспериментальная функция распределения (рис. 4.3, б), где hj – частота попадания случайного фактора y в j -й интервал; yj – значение случайного фактора, соответствующего крайней правой точке j-го интервала;  – величина интервалов;
– величина интервалов;  – накопленная частота попадания случайного фактора y в интервалах от 0 до
– накопленная частота попадания случайного фактора y в интервалах от 0 до  .
.

Рис. 4.3. Получение случайных чисел на основе экспериментального
закона распределения
Для равных интервалов
 , где j – номер интервала. (4.2)
, где j – номер интервала. (4.2)
Как видно из рис. 4.3, б, для получения случайного числа yk с заданным законом распределения необходимо, получая случайные числа xk, равномерно распределенные в интервале (0 – 1), проверять начиная с j = 1 неравенство
 . (4.3)
. (4.3)
Если неравенство не выполняется, j увеличивается на единицу. При выполнении неравенства случайное число yk получается в соответствии с (4.2) и (4.3) по формуле
 .
.
Если имеется возможность получить тем или иным способом аналитическую запись закона f(y), аппроксимирующего экспериментальное частотное распределение, можно использовать следующий прием.
Преобразуем распределение f(y) (рис. 4.4.,  ) таким образом, чтобы оно вписалось в единичный квадрат (рис. 4.4,б), для чего введем новую переменную
) таким образом, чтобы оно вписалось в единичный квадрат (рис. 4.4,б), для чего введем новую переменную
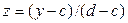 .
.

Рис. 4.4. Получение случайных чисел методом единичного квадрата
Проведя смещение и сжатие по оси координат и деля конкретное распределение f(z) на fmax, получим
 .
.
Тогда, выбирая пару случайных чисел, равномерно распределенных в квадрате (1, 1), проверяем, лежит ли точка с координатами (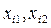 ) под кривой распределения f(z), т.е.
) под кривой распределения f(z), т.е.
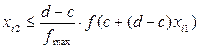 .
.
Если да, то значение случайной величины рассчитывается по формуле
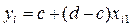 .
.
В противном случае число отбрасывается и выбирается следующая пара чисел  .
.
Аналогично вышеописанным способом могут быть построены процедуры формирования случайных значений дискретных величин. Например, необходимо получить случайные числа m, имеющие распределение Пуассона:
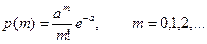 ..
..
Для этого необходимо взять случайное число xi и проверить справедливость неравенства
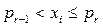 , (4.4)
, (4.4)
где  .
.
Если неравенство (4.4) не выполняется, то r увеличивается на единицу; при выполнении неравенства искомое случайное число m принимается равным r (рис. 4.5)

Рис. 4.5. Принцип получения дискретных случайных чисел





 (4.1)
(4.1)
 и
и  :
: ;
; .
. :
: .
. .
. получаемого закона при достаточно большом числе случайных n будут определяться следующими выражениями:
получаемого закона при достаточно большом числе случайных n будут определяться следующими выражениями:
 и среднеквадратического отклонения
и среднеквадратического отклонения 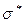 , то требуемые случайные числа yk получаются по формуле
, то требуемые случайные числа yk получаются по формуле ,
, – величина интервалов;
– величина интервалов;  – накопленная частота попадания случайного фактора y в интервалах от 0 до
– накопленная частота попадания случайного фактора y в интервалах от 0 до  .
.
 , где j – номер интервала. (4.2)
, где j – номер интервала. (4.2) . (4.3)
. (4.3) .
.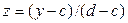 .
.
 .
.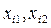 ) под кривой распределения f(z), т.е.
) под кривой распределения f(z), т.е.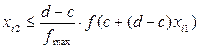 .
.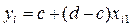 .
. .
.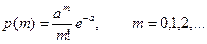 ..
..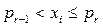 , (4.4)
, (4.4) .
.



