При обработке выходной информации стохастических имитационных моделей чаще всего решают следующие задачи:
 определение основных параметров полученной случайной выборки выходных данных (т.е. средних, дисперсии и т.д.);
определение основных параметров полученной случайной выборки выходных данных (т.е. средних, дисперсии и т.д.);
 определение формы и параметров закона распределения выходных характеристик;
определение формы и параметров закона распределения выходных характеристик;
 определение статистической зависимости между входами и выходами модели и проверка существенности полученной связи.
определение статистической зависимости между входами и выходами модели и проверка существенности полученной связи.
Для решения этих задач привлекается один из основных разделов математической статистики – теория испытания статистических гипотез. Смысл проверки статистических гипотез состоит в том, чтобы по имеющимся данным (случайной выборке) принять наиболее обоснованное решение о виде или параметрах генеральной совокупности.
Статистические критерии – показатели, вычисляемые на основе фактических наблюдения и дающие основание для суждения и приемлемости некоторых гипотез. При суждении о параметрах генеральной совокупности по определенному статистическому критерию принимают заранее некоторую наибольшую вероятность ошибки исследователя  . Эта вероятность называется уровнем значимости. В зависимости от важности рассматриваемого вопроса уровень значимости может принимать значения от 0,01 до 0.001 и даже выше. Дополнительная до 1 вероятность
. Эта вероятность называется уровнем значимости. В зависимости от важности рассматриваемого вопроса уровень значимости может принимать значения от 0,01 до 0.001 и даже выше. Дополнительная до 1 вероятность  называется доверительной вероятностью.
называется доверительной вероятностью.
В соответствии с уровнем значимости устанавливаются доверительные границы, в которых, судя по имеющимся статистическим данным, должен лежать искомый параметр генеральной совокупности. Эти границы (доверительные интервалы) будут тем уже, чем больше значений в имеющейся выборке и чем меньше доверительная вероятность. При этом считается, что все рассматриваемые данные имеют одинаковую точность измерений.
Определение выборочного среднего и выборочной дисперсии случайной выборки статистических данных проводится в следующем порядке:
выборочное среднее 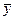 случайных величин
случайных величин 
 ,
,
где yj – j - е значение случайной величины y; m – объем статистических данных – число замеренных значений случайной величины y;
выборочная дисперсия равна квадрату эмпирического стандарта S, являющегося аналога среднеквадратической ошибки при конечном числе статистических данных:
 ;
;
для заданной доверительной вероятности p по таблицам математической статистики определяется значение критерия Стьюдента  , зависящее от доверительной вероятности p и объема имеющихся статистических данных (k = m -1);
, зависящее от доверительной вероятности p и объема имеющихся статистических данных (k = m -1);
определяются симметричные доверительные оценки выборочной средней, имеющие вид неравенства
 ,
,
где Y – математическое ожидание случайной величины y.
Критерий Стьюдента используется для определения доверительных интервалов в случае небольшого количества статистических данных  . При m больше 20 для определения доверительного интервала используется правило трех сигм:
. При m больше 20 для определения доверительного интервала используется правило трех сигм:  ;
;
Доверительную оценку средней квадратической ошибки  записывают в виде оценки относительного отклонения оцениваемого значения
записывают в виде оценки относительного отклонения оцениваемого значения  от эмпирического стандарта S:
от эмпирического стандарта S:
 ,
,
где значение доверительного коэффициента 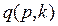 находится в зависимости от доверительной вероятности p и числа имеющихся статистических данных (k = m - 1) по соответствующим таблицам.
находится в зависимости от доверительной вероятности p и числа имеющихся статистических данных (k = m - 1) по соответствующим таблицам.
Проверка гипотез о законе распределения выходных характеристик проводится аналогично решению этой задачи для входных случайных величин. Для этого статистические данные группируются по интервалам таким образом, чтобы эти интервалы покрывали весь диапазон изменения исследуемого фактора y, длины интервалов были равны и чтобы количество данных в каждом интервале было достаточно большим (во всяком случае, не менее 5). Для каждого интервала (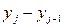 ) подсчитывается число mj результатов измерений попавших в этот интервал. После чего переходят к вычислению относительных частот hj попадания измеряемого параметра в интервал по формуле
) подсчитывается число mj результатов измерений попавших в этот интервал. После чего переходят к вычислению относительных частот hj попадания измеряемого параметра в интервал по формуле
 .
.
Графическое построение полученного экспериментального распределения относительных частот позволяет подобрать наиболее близкий к нему по форме теоретический закон распределения, после чего определяются числовые значения параметров аппроксимирующей функции – теоретического закона распределения. Далее необходимо проверить гипотезу о соответствии выбранного теоретического закона распределения и распределения в генеральной совокупности с помощью критериев согласия, позволяющих на основании доверительных интервалов сделать вывод о ее опровержении или неопровержении.
Из всех критериев согласия наиболее часто применяется критерий 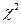 (критерий Пирсона):
(критерий Пирсона):
 ,
,
где  – теоретическая частота попадания случайной величины в интервал
– теоретическая частота попадания случайной величины в интервал  – число равных интервалов, но которые разбивается диапазон изменения исследуемой случайной величины.
– число равных интервалов, но которые разбивается диапазон изменения исследуемой случайной величины.
По соответствующим математико-статистическим таблицам находят при данном числе степеней свободы k и доверительной вероятности pкритическое значение критерия  . Гипотеза о соответствии экспериментального закона распределения теоретическому считается непротиворечивой опыту при условии
. Гипотеза о соответствии экспериментального закона распределения теоретическому считается непротиворечивой опыту при условии  .
.
При использовании критерия 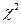 необходимо, чтобы объем экспериментальных данных был больше 50, а количество их в каждом интервале – более 5. В ряде случаев в качестве критериев согласия используются и другие статистические критерии, например критерий Колмогорского, Ястремского, критерий w2. Более подробно с вопросами построения теоретических законов распределения и их проверки с помощью критериев согласия можно ознакомиться в литературе по математической статистике.
необходимо, чтобы объем экспериментальных данных был больше 50, а количество их в каждом интервале – более 5. В ряде случаев в качестве критериев согласия используются и другие статистические критерии, например критерий Колмогорского, Ястремского, критерий w2. Более подробно с вопросами построения теоретических законов распределения и их проверки с помощью критериев согласия можно ознакомиться в литературе по математической статистике.
Для определения статистической зависимости между исследуемыми величинами и проверки полученной связи используют аппарат однофакторного и многофакторного регрессионного анализа. Эта задача эквивалентна решению задачи идентификации, где в качестве объекта рассматривается сама имитационная модель. В связи с тем, что при проведении экспериментов на ЭВМ неясно, какая из функций наилучшим образом описывает получающиеся данные, выбирают несколько таких функций, исходя из предположений о картине протекания исследуемого процесса:
 ,
,
где w – некоторая выходная характеристика модели; х – вектор входных параметров модели; f1,…,fS – различные математические функции, описывающие взаимосвязь выхода w со входами 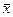 ;
;  – векторы параметров для соответствующих функций.
– векторы параметров для соответствующих функций.
После нахождения параметров  необходимо оценить качества полученной модели путем получения доверительных оценок параметров и доверительной оценки отклонения теоретической зависимости от экспериментальных данных. Например, для линейной зависимости результативного признака от факторного х теоретическую прямую можно записать в виде
необходимо оценить качества полученной модели путем получения доверительных оценок параметров и доверительной оценки отклонения теоретической зависимости от экспериментальных данных. Например, для линейной зависимости результативного признака от факторного х теоретическую прямую можно записать в виде
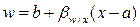 ,
,
где  .
.
Значимость эмпирического коэффициента корреляции r проверяется путем сравнения абсолютного значения коэффициента корреляции, умноженного на 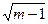 , с его критическими значениями
, с его критическими значениями  при заданной доверительной вероятности p. Если
при заданной доверительной вероятности p. Если  , то случайные величины коррелированы между собой. Критические значения
, то случайные величины коррелированы между собой. Критические значения  для различного объема статистических измерений и различных доверительных вероятностей p приведены в соответствующей литературе по математической статистике.
для различного объема статистических измерений и различных доверительных вероятностей p приведены в соответствующей литературе по математической статистике.
Доверительными границами для b служат
 ,
,
а для  –
–
 ,
,
где  – среднее арифметическое величины w;
– среднее арифметическое величины w;  – эмпирические стандарты величин w и k; t = t(p,k) – значение критерия Стьюдента для заданной доверительной вероятности p и числа степеней свободы k = m – 2.
– эмпирические стандарты величин w и k; t = t(p,k) – значение критерия Стьюдента для заданной доверительной вероятности p и числа степеней свободы k = m – 2.





 определение основных параметров полученной случайной выборки выходных данных (т.е. средних, дисперсии и т.д.);
определение основных параметров полученной случайной выборки выходных данных (т.е. средних, дисперсии и т.д.); . Эта вероятность называется уровнем значимости. В зависимости от важности рассматриваемого вопроса уровень значимости может принимать значения от 0,01 до 0.001 и даже выше. Дополнительная до 1 вероятность
. Эта вероятность называется уровнем значимости. В зависимости от важности рассматриваемого вопроса уровень значимости может принимать значения от 0,01 до 0.001 и даже выше. Дополнительная до 1 вероятность  называется доверительной вероятностью.
называется доверительной вероятностью.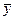 случайных величин
случайных величин 
 ,
, ;
; , зависящее от доверительной вероятности p и объема имеющихся статистических данных (k = m -1);
, зависящее от доверительной вероятности p и объема имеющихся статистических данных (k = m -1); ,
, . При m больше 20 для определения доверительного интервала используется правило трех сигм:
. При m больше 20 для определения доверительного интервала используется правило трех сигм:  ;
; записывают в виде оценки относительного отклонения оцениваемого значения
записывают в виде оценки относительного отклонения оцениваемого значения  ,
,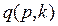 находится в зависимости от доверительной вероятности p и числа имеющихся статистических данных (k = m - 1) по соответствующим таблицам.
находится в зависимости от доверительной вероятности p и числа имеющихся статистических данных (k = m - 1) по соответствующим таблицам.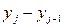 ) подсчитывается число mj результатов измерений попавших в этот интервал. После чего переходят к вычислению относительных частот hj попадания измеряемого параметра в интервал по формуле
) подсчитывается число mj результатов измерений попавших в этот интервал. После чего переходят к вычислению относительных частот hj попадания измеряемого параметра в интервал по формуле .
.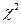 (критерий Пирсона):
(критерий Пирсона): ,
, – теоретическая частота попадания случайной величины в интервал
– теоретическая частота попадания случайной величины в интервал  – число равных интервалов, но которые разбивается диапазон изменения исследуемой случайной величины.
– число равных интервалов, но которые разбивается диапазон изменения исследуемой случайной величины. . Гипотеза о соответствии экспериментального закона распределения теоретическому считается непротиворечивой опыту при условии
. Гипотеза о соответствии экспериментального закона распределения теоретическому считается непротиворечивой опыту при условии  .
. ,
,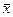 ;
;  – векторы параметров для соответствующих функций.
– векторы параметров для соответствующих функций.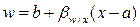 ,
, .
.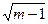 , с его критическими значениями
, с его критическими значениями  при заданной доверительной вероятности p. Если
при заданной доверительной вероятности p. Если  , то случайные величины коррелированы между собой. Критические значения
, то случайные величины коррелированы между собой. Критические значения  ,
, –
– ,
, – среднее арифметическое величины w;
– среднее арифметическое величины w;  – эмпирические стандарты величин w и k; t = t(p,k) – значение критерия Стьюдента для заданной доверительной вероятности p и числа степеней свободы k = m – 2.
– эмпирические стандарты величин w и k; t = t(p,k) – значение критерия Стьюдента для заданной доверительной вероятности p и числа степеней свободы k = m – 2.


