Однако следует отметить, что задача создания строгого формально-логического подхода к проблеме эксперимента на языке математики пока недостижима, так как любой эксперимент в значительной мере связан с эвристической деятельностью.
Рассмотрим критерии оптимальности факторных планов, позволяющие оценить коэффициенты регрессии. Для этого обратимся, например, к матрице планирования – условному обозначению сочетаний уровней переменных факторов, соответствующих условиям проведения отдельных экспериментов (рис. 3.1), и рассмотрим эти условия.
| k
N
| Переменные факторы
|
| x1
| x2
| x3
|
|
| –1
| –1
| –1
|
|
| –1
| –1
| +1
|
|
| –1
| +1
| –1
|
|
| –1
| +1
| +1
|
|
| +1
| –1
| –1
|
|
| +1
| –1
| +1
|
|
| +1
| +1
| –1
|
|
| +1
| +1
| +1
|
Рис. 3.1. Матрица планирования двухуровнего
трехфакторного эксперимента
1. Условие ортогональности, обеспечивающее получение независимых оценок коэффициентов регрессии и их дисперсий.
1.1. Условие ортогональности к столбцу или условие симметричности гласит: “Алгебраическая сумма элементов любого столбца матрицы планирования равна нулю”, т.е. планы симметричны относительно центра эксперимента.
 , (3.1)
, (3.1)
где j – номер фактора; i – номер опыта (серии опытов).
1.2. Условие парной ортогональности: “Сумма почленных произведений двух любых разных столбцов матрицы планирования равна нулю”.
 , k¹j. (3.2)
, k¹j. (3.2)
Это свойство позволяет упрощать или усложнять модели, исключая или добавляя коэффициенты без пересчета уже найденных параметров.
2. Условие нормировки: сумма квадратов элементов любого i-го столбца матрицы равна числу опытов (серий опытов) – N.
 . (3.3)
. (3.3)
В соответствии с этим положением коэффициенты уравнения регрессии определяются формулами:
 , (j = 1, 2, 3...k), (3.4)
, (j = 1, 2, 3...k), (3.4)
а их дисперсия
 , (3.5)
, (3.5)
где  - дисперсия воспроизводимости опытов; n – число параллельных опытов.
- дисперсия воспроизводимости опытов; n – число параллельных опытов.
3. A – оптимальность (от английского термина average variance – средняя дисперсия) соответствует планам с минимальной средней дисперсией оценок коэффициентов регрессии.
4. D – оптимальность (по начальной букве английского слова determinant– определитель) обеспечивает минимум обобщенной дисперсии всех оценок коэффициентов регрессии.
5. E – оптимальность (от английского eigen value – собственное значение) не допускает наличие слишком больших дисперсий у некоторых оценок коэффициентов регрессии.
Критериями оптимальности планов, связанных с ошибками в оценке поверхности отклика, будут следующие.
6. Насыщенность плана – приближение числа опытов к числу коэффициентов уравнения регрессии. Этот критерий вступает в противоречие с желанием экспериментатора максимально сократить число опытов.
7. Композиционность – возможность перехода от простых моделей к более сложным при сохранении результатов первоначальных шагов.
8. Ротатабельность (от английского rotatable – способный к вращению) – это наличие одинаковой дисперсии во всех направлениях факторного пространства на равных расстояниях от центра плана.
9. G – оптимальность (от английского general variance – общая дисперсия) минимизирует максимально возможную дисперсию предсказаний – дисперсию экстраполированных (продолженных за рамки эксперимента) значений выхода.
10. Q – оптимальность минимизирует среднюю дисперсию предсказаний.
11. Возможность преобразования независимых факторов (переменных) при сохранении оптимальности плана.
Следует отметить, что существует еще более 10 критериев оптимальности факторных планов, но они менее важны.
Задачи, решаемые факторными планами
Все экспериментальные задачи, решаемые с помощью оптимальных факторных планов, можно разделить на две группы:
- оптимизационные или экстремальные задачи,
- задачи описания или интерполяционные.
Оптимизационные задачи связаны с нахождением экстремума поверхности отклика, обеспечивающего оптимальное функционирование рассматриваемой системы.
Например, оптимизация состава синтезируемого соединения.(например сорбента). Факторами являются процентное содержание компонентов, а выходом – наибольшая сорбцинная способность. Здесь величина экстремума выхода и оптимальные значения факторов заранее неизвестны. Для подобных задач характерны несколько случаев.
1. Имеется несколько экстремумов. Здесь среди частных экстремумов необходимо найти глобальный.
2. Оптимальная величина параметра оптимизации имеет нечисловое одностороннее логическое ограничение. Например, привес бройлеров или минимум себестоимости изделия. Понятно, что нельзя обеспечить привес бройлера больше, чем вес курицы, или свести себестоимость к нулю. Однако, строго говоря, в нашем случае ограничение отсутствует, так как оптимизируемые характеристики могут изменяться бесконечно, но при уменьшении величины этого изменения.
3. Оптимум выхода имеет конкретное одностороннее физическое ограничение. Например, выход годного на литье или расход моечного раствора. Известно, что выход годного не может превысить 100%, а минимальная норма моечного раствора должна обеспечивать смачивание всей очищаемой поверхности. Здесь оптимум асимптотически приближается к ограничению, но не должен когда-либо его превысить.
Наконец, оптимум может носить качественный характер одного из нескольких вариантов (технологических процессов, конструкций аппаратов, работы операторов).
Для каждого случая имеется некоторая оптимальная стратегия, но не всегда формализованная, а чаще всего основанная на опыте и интуиции экспериментатора.
Задачи описания носят интерполяционный характер. Формируется расчетная формула – модель для определения параметра выхода в любой точке исследованного диапазона факторов. Например, формула механической обработки, связывающая скорость резания V с глубиной t, подачей S и стойкостью инструмента T:
 . (3.6)
. (3.6)
Иногда, если невозможно поставить эксперимент во всем рассматриваемом диапазоне факторного пространства, полученные модели используют для экстраполяции выхода, прогнозирования поведения системы. Оценка точности результатов осуществляется дисперсией предсказаний, а план эксперимента должен обладать ротатабельностью.
Наконец, для экстремальных зависимостей, когда известен оптимум выхода и его допустимые колебания, интерполяционная (линеаризованная или квадратичная) модель позволяет рассчитать допустимый разброс факторов, обеспечивающих колебание выхода в заданных пределах.
В зависимости от степени кривизны поверхности отклика она может быть описана линейной функцией относительно переменных и нелинейной, например, квадратичной. Выбор плана экспериментальных исследований при отсутствии априорной информации осуществляется на основе личного опыта исследователя.
Таким образом, экспериментатор обосновывает тип задачи, выбор оптимального плана, его реализацию и принятие соответствующих решений после анализа полученных результатов.
Критерий оптимизации
При постановке оптимизационных задач очень важно правильно определить параметр, который требуется оптимизировать. Эта часть исследований не поддается формализации и целиком зависит от опыта и интуиции исследователя.
Параметр оптимизации является реакцией (откликом) исследуемой системы на воздействие факторов. Поскольку реакция любого объекта исследований весьма многогранна, необходимо выбрать аспект реакции, представляющий наибольший интерес, то есть параметр оптимизации является количественной характеристикой цели исследований.
В качестве оптимизируемых характеристик в различных системах могут быть выбраны следующие параметры:
1. Технологические, связанные с процессом производства (жирность молока, твердость металла),
2. Конструктивные, определяющие конструкцию (зазор в подшипнике скольжения, толщина стен строения),
3. Материаловедческие, характеризующие свойства используемых материалов (прочность кирпича, негорючесть облицовки).
4. Эксплуатационные, служащие оценкой работы системы (ресурс двигателя, износостойкость подошвы).
5. Экономические (себестоимость, рентабельность).
Предпочтительно использовать количественные параметры, но могут быть выбраны и качественные:
– тип технологического процесса изготовления какой-либо детали;
– различные конструкции некоторого узла;
– марка или структура применяемого материала;
– ремонтопригодность или резервируемость;
– необходимость в капитальных затратах.
Для перевода качественных параметров в количественные может быть использован, например, ранговый подход или разбиение матрицы экспериментального плана на блоки.
Движение в факторном пространстве к оптимуму возможно, если выбран один единственный параметр оптимизации. При наличии нескольких параметров (например, точность, себестоимость, ресурс) все, кроме одного, выступают уже не параметрами оптимизации, а ограничениями (оптимум ресурса при установленной точности и себестоимости).
Основные требования к параметру оптимизации можно сформулировать в следующем виде:
1 – параметр оптимизации должен быть количественным;
2 – измеряемым;
3 – должен выражаться одним числом (например, соотношение компонентов A: B = 3: 2 выражается одним числом – 1,5);
4 – быть однозначным в статистическом смысле (заданному набору факторов соответствует одно значение выхода);
5 – эффективным в статистическом смысле, т.е. определяемым с наибольшей достижимой точностью;
6 – существующим для всех исследуемых состояний системы (область его определения может иметь ограничения);
7 – универсальным или обладать полнотой – способностью всесторонне характеризовать объект;
8 – с конкретным физическим смыслом (по возможности);
9 – простым и легко вычисляемым.
Требование физического смысла связано с последующей интерпретацией результатов экспериментов. Легко понять термины "наибольшая производительность" или "точность". Но когда для параметров выхода не выполняется требование статистической эффективности (например, однородность дисперсий), прибегают к преобразованию выхода. Например: ln y или sin 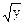 и становится неясным, что значит экстремум выхода.
и становится неясным, что значит экстремум выхода.
Практически всегда результаты исследования сложных объектов могут быть представлены как задачи с несколькими выходными параметрами. В этом случае можно получить математические модели для каждого параметра выхода, но оптимизировать одновременно несколько функций невозможно.
Из положения можно выйти двумя способами: обосновать отказ от всех выхо-дов, кроме одного, или ввести новый единый обобщенный критерий.
В первом случае можно выбрать одну наиболее важную функцию, исходя из опыта исследователя и целей эксперимента, или воспользоваться данными корреляционного анализа. При этом между всевозможными парами параметров вычисляется коэффициент парной корреляции – мера связи между двумя случайными величинами. Сильная корреляционная связь (более 0,8) при высокой достоверности (обычно 0,95 при числе степеней свободы f = N – 2) позволяет исключить из рассмотрения любой из двух анализируемых параметров как не содержащий дополнительной информации об объекте исследований.
Гораздо перспективнее представляется второй путь – введение обобщенного параметра оптимизации. Для этого необходимо предварительно решить три вопроса:
- привести все параметры выхода к сравнимому безразмерному виду,
- ввести для всех параметров однотипную шкалу измерений,
- выбрать правило объединения нескольких частных откликов в единый обобщенный.
Переменные факторы
Исследование любого объекта – это изучение его реакции на внешние воздействия или факторы. Следовательно, фактор представляет собой измеряемую переменную величину, принимающую в некоторый момент времени определенное дискретное значение.
Каждый фактор имеет область определения – совокупность множества значений, которые он может принимать.
Факторы могут быть количественными (величина погрешности, твердость материала и т.п.) и качественными (различные технологические процессы, разные операторы и т.п.). Качественные факторы могут быть переведены в количественные, например, ранжированием.
Факторы могут быть размерными (прочность, процентный состав) и безразмерными (ранг, относительная деформация); с дискретной областью определения (размеры) и непрерывной (время, температура). В последнем случае экспериментатор выбирает некоторое множество дискретных значений фактора, называемых уровнями.
Выбор уровней факторов и, в значительной степени, отбор значимых факторов из их общего количества является неформализованной эвристической задачей (несмотря на априорную информацию). Решение подобных задач целиком зависит от интуиции и опыта экспериментатора.
Факторы должны быть управляемыми, т.е. позволять исследователю устанавливать требуемое значение (уровень) фактора и поддерживать его постоянство в течение всего эксперимента.
Рассмотрим процесс измерения некоторой величины и влияние внешних факторов на его точность. Управляемыми факторами можно считать точность измерительных приборов, квалификацию (разряд) исследователя, освещенность рабочего места и проч. К неуправляемым факторам можно отнести самочувствие оператора, температуру и влажность в лаборатории т.п. Очевидно, что при планировании экспериментальных исследований возможен учет только управляемых факторов, а неуправляемые следует отнести к шумовому полю путем рандомизации опытов.
Все факторы должны быть однозначными, т. е. не являться функциями других факторов. В противном случае их трудно, а зачастую невозможно поддерживать на установленных уровнях. Примерами однозначных факторов являются температура, размер, давление; неоднозначных – погрешность, характер температурной функции в реакторе. В последнем случае можно добиться однозначности, используя при линейном росте температуры тангенс угла наклона прямой, а при нелинейном или смешанном законе – номер температурной кривой.
Все используемые в эксперименте факторы должны быть независимы, т.е. любой уровень каждого фактора может быть установлен независимо от величины уровней остальных факторов. Если это условие невыполнимо, то невозможно планировать эксперимент.
Например, в некоторой термодинамической системе при выполнении закона Менделеева–Клапейрона (p×V = c×T) нельзя одновременно независимо установить давление P, объем V и температуру T, так как по любым двум факторам может быть вычислен третий. Поэтому в план эксперимента можно включить лишь два любых фактора: P и V, P и T, V и T. Иными словами, между выбранными и включенными в план эксперимента факторами не должно быть линейной корреляционной зависимости.
Выбранные факторы должны быть совместимы, т.е. все их комбинации являются осуществимыми и безопасными. Несовместимым будет попытка сплавить олово и графит. Несовместимо воздействие на глицерин смеси серной и азотной кислот, могущее привести к взрыву образовавшегося нитроглицерина. Иногда добиться совместимости факторов можно уменьшением диапазона их варьирования.
Наконец, следует иметь в виду, что точность фиксации уровней должна быть выше, чем точность измерения параметра оптимизации. В противном случае возникают затруднения (статистическая неоднородность, значительная погрешность выхода) в обработке результатов эксперимента.
Для успешного выбора основного (нулевого), а также наибольшего и наименьшего уровней факторов необходимо учитывать априорную информацию о точности фиксирования факторов, погрешность параметра оптимизации, интенсивность влияния того или иного фактора на выход.
При выборе диапазона варьирования отобранных факторов начинают с назначения основного уровня (центра экспериментального плана). При оптимизационных задачах в качестве него выбирают оптимум выходного параметра, а первоначальный интервал варьирования факторов выбирают небольшим. Это позволяет получать линейные модели и выработать стратегию пошагового движения к оптимуму.
При интерполяционном характере экспериментальных задач стараются как можно больше расширить диапазон варьирования. При этом, как правило, получаются нелинейные регрессионные модели.
В зависимости от соотношения интервал варьирования – область определения фактора различают узкий – 0,0, средний – 0,3 и широкий – более 0,3 интервалы.
Необходимое число уровней факторов выбирают в общем случае в зависимости от кривизны поверхности отклика в факторном пространстве. Необходимо помнить, что количество уровней фактора влияет на порядок полиномиальной модели, а количество опытов определяется формулой
N = Mk, (3.7)
где M – число уровней каждого фактора; k – число переменных факторов в эксперименте.
Нулевой или средний уровень фактора может быть найден из выражения
 , (3.8)
, (3.8)
где  ,
,  ,
, 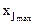 – соответственно наименьший, средний и наибольший уровни j-го фактора.
– соответственно наименьший, средний и наибольший уровни j-го фактора.
Величина интервала варьирования фактора рассчитывается по формуле
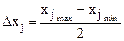 . (3.9
. (3.9
Следует отметить, что интервал варьирования не должен быть меньше погрешности, с которой фиксируется уровень фактора.
С целью облегчения и упрощения расчетов при обработке экспериментальных результатов, а также для возможности использования стандартных планов экспериментов факторы кодируются. При этом все вычисления производятся в безразмерной системе координат – кодированной системе. Наибольшему уровню фактора присваивается обозначение “+1”, наименьшему “–1”, а среднему “0”.
Кодирование – это линейное преобразование натуральных (размерных) уровней факторов в кодовые безразмерные величины. Переход от натуральных xj к кодированным Xj переменным осуществляется по формуле
 . (3.10)
. (3.10)
Кодированное пространство (при числе факторов-осей более трех – гиперпростран-ство), на осях которого откладываются значения варьируемых факторов, называется факторным.
Таким образом, при решении оптимизационных задач мы находим экстремум пара-метра оптимизации, а при решении интерполяционных задач – описываем процесс его изменения в факторном пространстве.
Планы полнофакторных экспериментов
В настоящее время отсутствует единая всеобъемлющая теория эксперимента. Выбор того или иного оптимального плана основывается в значительной степени на опыте исследователя и логике исследований. Математическая теория эксперимента не дает однозначно оптимальных решений.
В зависимости от задач исследований свойств объекта, выполнения математических ограничений и т.п. можно выбрать тот или иной класс планов – стратегию научного поиска.
Одна из классификаций планов выглядит следующим образом:
- планы дисперсионного анализа;
- планы отсеивающего эксперимента;
- планы многофакторного анализа;
- планы для изучения поверхности отклика;
- планы для динамических задач;
- планы для изучения механизма явлений;
- планы для построения диаграмм состав – свойство.
По методу анализа и виду математической модели все планы можно разбить на три группы: планы дисперсионного, регрессионного и ковариационного анализа.
По числу уровней переменных факторов планы бывают 2х-, 3х- и более уровневые. Кроме того, различают планы первого порядка для построения линейных моделей, второго – для квадратичных моделей и планы высших порядков. В настоящее время наиболее освоены и распространены симметричные двухуровневые планы типа 2k, где k – число факторов. Эти планы имеют одновременно все критерии оптимальности.
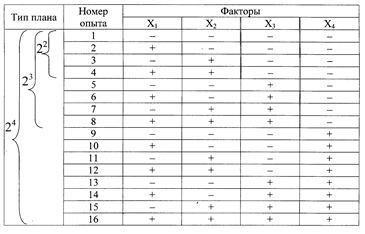
Планы изображаются в виде матриц планирования – таблиц, где наибольшее значение фактора обозначено “+”, а наименьшее “–” (рис.3.5).
Каждый столбец в матрице планирования называется вектор-столбцом, а строка – век-тор-строкой.
Логика построения матриц планирования двухуровневых полнофакторных экспериментов очевидна: необходимо повторить предыдущий план на наименьшем и наибольшем уровнях добавляемого исследуемого фактора.
Рис. 3.5. Матрицы полного факторного двухуровнего эксперимента
(2-4 фактора)





 , (3.1)
, (3.1) , k¹j. (3.2)
, k¹j. (3.2) . (3.3)
. (3.3) , (j = 1, 2, 3...k), (3.4)
, (j = 1, 2, 3...k), (3.4) , (3.5)
, (3.5) - дисперсия воспроизводимости опытов; n – число параллельных опытов.
- дисперсия воспроизводимости опытов; n – число параллельных опытов. . (3.6)
. (3.6)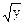 и становится неясным, что значит экстремум выхода.
и становится неясным, что значит экстремум выхода. , (3.8)
, (3.8) ,
,  ,
, 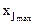 – соответственно наименьший, средний и наибольший уровни j-го фактора.
– соответственно наименьший, средний и наибольший уровни j-го фактора.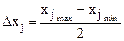 . (3.9
. (3.9 . (3.10)
. (3.10)