Інші критерії якості лінійної регресії

 

Припустимо, відомі n прогнозних даних 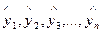, що відповідають n

реальним даним у₁, у₂, у₃, …, у_n, тобто маємо відповідно n помилок прогнозу е₁, е₂, е₃, …, е_n . Для визначення якості прогнозу (моделі) на практиці широко використовуються такі критерії:

:

1. Середня помилка прогнозу:

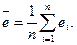                                                            (2.5.1)

Цей критерій характеризує ступінь зміщення прогнозу і для правильних прогнозів повинен прямувати до 0 за умови великої кількості спостережень, тобто

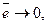при .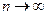

 

2. Дисперсія помилок:

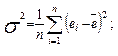                                                   (2.5.2)

та стандартне відхилення:

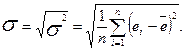                                 (2.5.3)

Цей критерій вимірює ступінь розкиду значень змінної навколо свого середнього значення.

Для простої лінійної регресії середнє значення помилок дорівнює нулеві. Тому

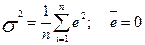.                                          (2.5.4)

 

 

3. Абсолютне середнє відхилення:

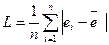.                                                  (2.5.5)

 

 

4. Середній квадрат помилки:

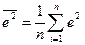. (2.5.6)

Цей критерій для лінійної регресії збігається з дисперсією помилок

 

.

5. Абсолютна середня процентна помилка:

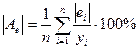.                                           (2.5.7)

 

Цей критерій використовується при порівнянні точності прогнозів різнорідних об’єктів, бо характеризує відносну точність прогнозу. При цьому вважається, якщо значення цього критерію менше 10% — висока точність прогнозу, а отже, і якість моделі; від 10 до 20% — добра точність; від 20 до 50% — задовільна точність; понад 50% — незадовільна точність

 

.

6. Середня процентна помилка:

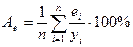.                                             (2.5.8)

 

Це показник незміщеності прогнозу. З точки зору практики для якісних моделей цей показник має бути малим, загалом не перевищувати 5%. Зазначимо, що як і показник 5, він не визначений для нульових значень у [5]

.

7. Середня абсолютна помилка:

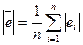
Примітка: Для розрахунку вищеперелічених критеріїв варто використати таблицю:

 

№
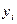
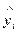
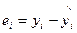
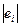
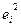
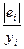
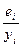
1 2 3 . . . n

 

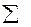
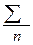
Завдання 17 . Перевірити якість лінійної регресійної моделі, побудованої в завданні 4, за допомогою критеріїв: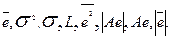

Зробити висновки.

 

Завдання 18. Перевірити якість лінійної регресійної моделі, побудованої в завданні 8, за допомогою критеріїв: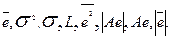

Зробити висновки.

 

Завдання 19. Перевірити якість лінійної регресійної моделі, побудованої в завданні 10, за допомогою критеріїв з розділу 2.5. Зробити висновки.

 

Завдання 20. Перевірити якість лінійної регресійної моделі, побудованої в завданні 11, за допомогою критеріїв з розділу 2.5. Зробити висновки.

 

 

2.6. Математичне сподівання та дисперсія розподілу параметрів  b ₀ та b ₁ . Оцінка дисперсії випадкової величини .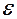

1. Математичне сподівання параметра b ₀ дорівнює:

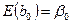.                                                (2.6.1)

             2. Дисперсія параметра b _0:

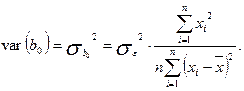    (2.6.2)

         3. Математичне сподівання параметра b ₁ дорівнює:

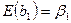.                                                (2.6.3)

 

   4. Дисперсія параметра b ₁ :

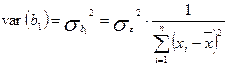,         (2.6.4)

де 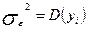 — дисперсія залежної змінної.

 

                5. Оцінка дисперсії випадкової величини :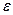

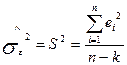,                                  (2.6.5)

де к — кількість параметрів, що оцінюється в регресійній моделі. Для простої лінійної регресії:

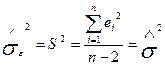.                         (2.6.6)

 

Середнє квадратичне відхилення оцінки дисперсії:

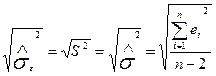.            (2.6.7)

Оскільки випадкова величина 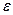 — неспостережувана, то і її дисперсію неможливо обчислити, тому на практиці дисперсія випадкової величини  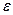замінюється на свою оцінку.

У виразах (2.6.2) та (2.6.4) дисперсія параметрів b₀ та b₁ — невідома, оскільки вона залежить від дисперсії помилок 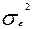 випадкової величини 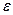, котру неможливо спостерігати. Отже, для параметрів b₀ та b₁ дійсна дисперсія замінюється своєю оцінкою [5]:

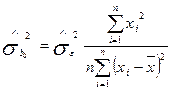;                       (2.6.8)

 

                         (2.6.9)

 

Приклад 5. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в прикладі 1.

Рішення:

  Для параметра b_1:

 

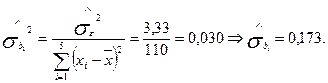
  Для параметра b_0:

 

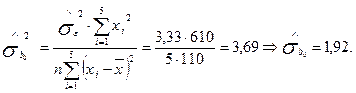
Завдання 21. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4.

 

Завдання 22 . Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8.

 

Завдання 23. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10.

 

Завдання 24. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11.

 

Завдання 25. Маємо таку інформацію:

 

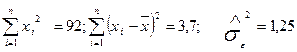; n = 40

 

а) визначити 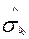;                  б) визначити .

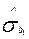2.7. Перевірка значимості параметрів b ₀  та b ₁ вибіркової лінійної регресійної моделі за допомогою t -теста Стьюдента

 

t -тест Стьюдента для перевірки значимості параметрів b₀ та b_1, визначених методом найменших квадратів, має вигляд:

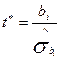.                           (2.7.1)

За таблицею t-розподілу Стьюдента визначають 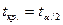 — критичне значення
з (n-2) ступенями вільності та 5%-рівнем значимості.

Якщо 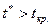, то параметр b_i — статистично значимий [5].

 

Приклад 6.  Перевірити значимість параметрів b₀ та b₁ лінійної регресійної

                 моделі, побудованої в прикладі 1, за допомогою

                 t-теста Стьюдента.      

 .  

Рішення:

 Для параметра b₁ та b₀:

_;

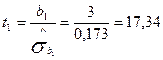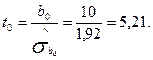
Примітк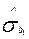а:  та 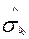 розраховані в прикладі 5. За таблицею t-розподілу Стьюдента визначимо 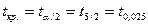— критичне значення з n-2=5-2=3 — ступенями вільності та 5%-рівнем значимості:

.

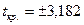Оскільки, t₁=17,34 > t_кр.=3,182;

t₂ = 5,21 > t_кр.=3,182.

Отже, параметри b₁ та b₀ статистично значимі.

 

Завдання 26. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4, використавши t-тест Стьюдента.

 

Завдання 27. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8, використавши t-тест Стьюдента.

 

Завдання 28. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10, використавши t-тест Стьюдента.

 

Завдання 29. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11, використавши t-тест Стьюдента.