Варіаційний ряд для прикладу 1

МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

“ХЕРСОНСЬКИЙ ДЕРЖАВНИЙ АГРАРНИЙ УНІВЕРСИТЕТ”

Кафедра вищої математики  та

                                                                                                       економічної кібернетики

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ  ТА ЗАВДАНН Я

ДЛЯ ПРОВЕДЕННЯ ПРАКТИЧНИХ ЗАНЯТЬ

 

            З КУРСУ “ЕКОНОМЕТРІЯ”

 

ДЛЯ СТУДЕНТІВ 2 КУРСУ

ЕКОНОМІЧНОГО ФАКУЛЬТЕТУ

 

       зі спеціальності:

6.050200

-  “Менеджмент організацій”

                                               

 

 

Херсон – 2010

Методичні рекомендації та завдання для проведення практичних занять з курсу “Економетрія” для студентів 2 курсу економічного факультету зі спеціальності: 6.050200 - “Менеджмент організацій”. Розглянуто та затверджено на засіданні кафедри вищої математики та економічної кібернетики протокол № 2 від “24” вересня 2010 року і схвалено навчально-методичною комісією спеціальності: “Менеджмент організацій” протокол № ____ від “___” _____________ 20____ року.

      

Рецензент: д.е.н., проф. Соловйов І.О.

Ас. Артамонова І.Ю. Методичні рекомендації та завдання для проведення практичних занять з курсу “Економетрія” для студентів 2 курсу економічного факультету зі спеціальності: 6.050200 - “Менеджмент організацій”. – Херсон, ДВНЗ “ХДАУ”, - 2010 р.

 

                                                                                            

Артамонова І.Ю. 2010

 

Інформаційна база економетричних моделей

 

Економетрія як наука насамперед ставить собі за мету обґрунтований аналіз економічних явищ на базі математико-статистичних методів. Такий аналіз потребує наявності числових характеристик економічних явищ та можливості вимірювання їх. При вимірюванні кількісних ознак можуть бути отримані два типи рядів даних — динамічні та варіаційні. Ці ряди здебільшого і становлять інформаційну базу економетричних моделей.

 

Динамічні ряди та їхні характеристики

Динамічним рядом називається послідовність спостережень за процесом або явищем у рівновіддалені проміжки часу.

Узагальненими характеристиками динамічного ряду є середній рівень ряду динаміки, середній абсолютний приріст, середній коефіцієнт (темп) зростання, середній коефіцієнт (темп) приросту.

Метод розрахунку середнього рівня ряду динаміки залежить від типу динамічного ряду. Для інтервальних динамічних рядів абсолютних показників середній рівень за досліджуваний період визначається за формулою простої середньої арифметичної:

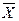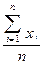 =                        (1.1.1),

де n — кількість рівнів ряду.

 

Приклад 1. Маємо інтервальний динамічний ряд абсолютних показників:

 

Роки	2006	2007	2008	2009	2010
Урожайність озимої пшениці, ц/га	25,2	26,7	13,6	28,1	30,9
Позначення	Х1	Х2	Х3	Х4	Х5

 

Визначити: Середній рівень урожайності озимої пшениці за період 2006-2010 роки.

Рішення: Середній рівень урожайності озимої пшениці дорівнює:

 

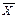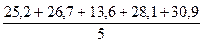 = = 24,9 ц/га

 

Середній рівень моментного динамічного ряду, коли проміжки між датами однакові, визначається за формулою середньої хронологічної:

 

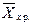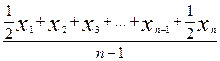 = ,           (1.1.2)

де n — кількість дат; Х₁, Х₂, Х₃, …, Х_n-1 X_n — рівні ряду в послідовні моменти часу.

Приклад 2. Маємо моментний ряд динаміки — чисельність робітників підприємства на перше число кожного місяця 2010 року:

          На 1.01.2010 – 800 осіб                               1.05.2010 - 824 осіб

1.02.2010 –804 осіб                               1.06.2010 - 820 осіб

1.03.2010 – 806 осіб                               1.07.2010 - 822 осіб

                1.04.2010 - 818 осіб

Визначити: Середню чисельність робітників за перше півріччя 2010 року.

Рішення: Середній рівень ряду за перше півріччя 2010 року дорівнює:

 

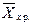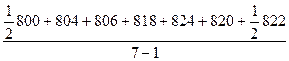
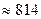= осіб.

 

Для визначення середнього рівня моментного ряду динаміки з неоднаковими проміжками між часовими датами використовується формула зваженої середньої арифметичної:

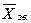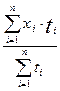 = ,   (1.1.3)

 

де t_i — кількість днів (місяців) між суміжними датами.

 

Середній абсолютний приріст показує, як швидко змінюється кінцевий рівень ряду відносно початкового:

 

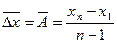, (1.1.4)

де 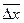;  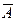— середній абсолютний приріст;

x_n, x₁ — кінцевий та початковий рівень ряду.

 

Приклад 3. Розрахувати для динамічного ряду урожайності озимої пшениці (приклад 1) середній абсолютний приріст за період 2006-2010 роки.

Рішення: 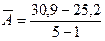 = 1,425 ц/га.

Середній коефіцієнт зростання характеризує середню швидкість зміни економічного процесу або явища і розраховується за формулою:

 

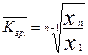,        (1.1.5)

 

де 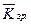— середній коефіцієнт зростання.

Середній коефіцієнт зростання, виражений у відсотках, називається середнім темпом зростання:

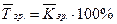, (1.1.6)

де 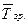— середній темп зростання.

 

Приклад 4. Визначити середній коефіцієнт (темп) зростання для динамічного ряду урожайності озимої пшениці (приклад 1) за період 2006-2010 роки.

Рішення: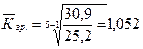

.

 

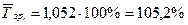Середній коефіцієнт приросту відрізняється від середнього коефіцієнта зростання на одиницю:

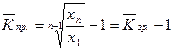, (1.1.7)

де 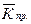— середній коефіцієнт приросту.

Середній коефіцієнт приросту, виражений у відсотках, називається середнім темпом приросту:

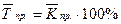, (1.1.8)

де 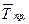— середній темп приросту.

 

Приклад 5. Розрахувати середній коефіцієнт (темп) приросту для динамічного ряду урожайності озимої пшениці (приклад 1) за період 2006-2010 роки.

Рішення:

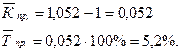
Показниками варіації рядів динаміки є: дисперсія, середнє квадратичне відхилення, коефіцієнт варіації.

Дисперсія показує середню суму квадратів відхилень рівнів ряду від середнього рівня і позначається 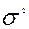або var(x):

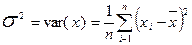,     (1.1.9)

де 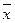— середній рівень динамічного ряду;

n — кількість спостережень.

Для того, щоб дисперсію можна було порівняти з середніми характеристиками, вводиться середнє квадратичне відхилення ( ):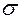

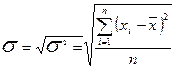. (1.1.10)

Для порівнювання ступеня коливання різнорідних показників у відсотках запроваджено інший показник — коефіцієнт варіації ( V ):

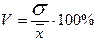,                  (1.1.11)

де V — коефіцієнт варіації; 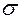— середнє квадратичне відхилення, 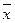— середній рівень ряду.

Приклад 6. Визначити показники варіації для динамічного ряду урожайності озимої пшениці (приклад 1) за період 2006-2010 роки.

Рішення: Дисперсія:

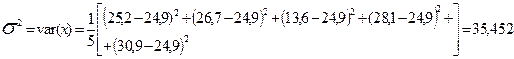
 Середнє квадратичне відхилення:

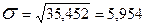ц/га

Коефіцієнт варіації:

.

 

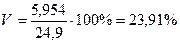Завдання 1. За даними урожайності картоплі за 11 років в сільськогосподарському підприємстві розрахувати:

а) середній рівень ряду динаміки;

б) середній абсолютний приріст;

в) середній коефіцієнт (темп) зростання;

г) середній коефіцієнт (темп) приросту;

д) дисперсію;

е) середнє квадратичне відхилення;

є) коефіцієнт варіації.

 

Роки	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
I варіант
Урожай-ність картоплі, ц/га	245	260	220	120	130	230	290	300	290	110	140
II варіант
Урожай-ність картоплі, ц/га	234	259	265	270	240	232	254	268	272	250	241
III варіант
Урожай-ність картоплі, ц/га	272	263	259	245	251	253	268	260	255	259	247

 

Завдання 2. За даними чисельності робітників підприємства на перше число кожного місяця 2009 року:

На 1.01.2009 р. — 198 осіб 1.02.2009 р. — 210 осіб 1.03.2009 р. — 213 осіб 1.04.2009 р. — 204 особи 1.05.2009 р. — 207 осіб 1.06.2009 р. — 215 осіб 1.07.2009 р. — 203 особи

1.08.2009 р. — 190 осіб 1.09.2009 р. — 185 осіб 1.10.2009 р. — 189 осіб 1.11.2009 р. — 209 осіб 1.12.2009 р. — 216 осіб 1.01.2010 р. — 205 осіб

 

Визначити середню чисельність робітників за перше та друге півріччя та за 2009 рік в цілому.

 

Завдання 3. За даними кількості внесення органічних добрив під картоплю в господарствах району за 13 років визначити:

а) середній рівень внесення органічних добрив під картоплю в районі за період з 1997 по 2009 роки;

б) середній абсолютний приріст;

в) середній коефіцієнт (темп) зростання;

г) середній коефіцієнт (темп) приросту;

д) дисперсію;

е) середнє квадратичне відхилення;

є) коефіцієнт варіації.

 

Роки	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
Внесено органічних добрив під картоплю, т/га	85	83	60	65	84	86	90	87	45	65	80	45	70

 

Завдання 4. За даними таблиці охарактеризувати динамічні ряди факторів Х₁,Х₂, Х₃, Х₄, Х₅, Х₆, розрахувавши для кожного з факторів:

а) середній рівень;

б) середній абсолютний приріст;

в) середній коефіцієнт (темп) зростання;

г) середній коефіцієнт (темп) приросту;

д) дисперсію;

е) середнє квадратичне відхилення;

є) коефіцієнт варіації.

 

Рік	*Кількість зареєстрова-них злочинів в Україні, тис., Х1	*Кількість населення України, млн.осіб, Х2	*Забезпече-ність житлом, м2 на особу, Х3	*Рівень освіти, осіб з освітою на 1000 осіб Х4	*Кількість міського населення, млн. осіб, Х5	*Продаж алкогольних напоїв, л на особу, Х6
1	2	3	4	5	6	7
2000 2001 2002 2003 2004 2005 2006 2007 2008 2009	250,0 249,6 248,7 237,8 243,0 322,3 369,8 405,5 480,5 539,3	50,7 50,8 51,0 51,2 51,4 51,7 51,8 51,9 52,1 52,2	16,0 16,3 16,8 17,1 17,3 17,6 17,8 18,0 18,2 18,5	877 884 894 903 912 928 939 951 962 974	33,2 31,4 33,7 34,2 34,7 34,6 34,8 35,1 35,3 35,4	5,3 5,2 3,4 2,9 3,2 3,8 4,1 4,1 3,6 3,3

 

*Джерело: “Статистичний щорічник України” (2009 р.).

 

Варіаційні ряди та їхні характеристики

Варіаційні ряди — це ряди даних, які показують кількісну міру певної ознаки у всіх об’єктах однієї сукупності.

Маємо варіаційний ряд: Х₁, Х₂, Х₃, …, Х_К,

де Х_i — числа, які показують зміну (варіацію) ознаки, що вивчається, і називаються варіантами;

і — номер варіанти (і = 1,2,3, …к).

 

Приклад 1. При обстеженні студентів 1-го курсу за віком було зафіксовано такі дані: 17,18,18,18,18,19,20,20,20,21,21,21,17,18,18,18,19,20,20,20,21,21,21,24.

Якщо впорядкувати ці дані у зростаючому або спадному порядку, то отримаємо ранжований ряд. Числа, які показують, скільки разів (як часто) зустрічаються окремі значення варіант, називаються частотами.

Позначимо частоту і-ї варіанти Х_і через n_i, тоді ранжований дискретний варіаційний ряд запишеться у вигляді:

 

Варіаційний ряд у загальному вигляді			Варіаційний ряд для прикладу 1
Номер: варіанти	Значення варіанти	Частота варіанти	Номер варіанти	Значення варіанти	Частота варіанти
1 2 . . . К	Х1 Х2 . . . Хк	n1 n2 . . . nк	1 2 3 4 5 6	17 18 19 20 21 24	2 7 2 6 6 1

 

Для варіаційного ряду є також дві групи характеристик: міри рівнів (середні) та міри розсіяння.

Найбільш поширеними середніми характеристиками для варіаційних рядів є середня арифметична, медіана і мода.

Для дискретного варіаційного ряду середня арифметична розраховується за формулою:

 

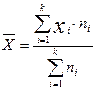,      (1.2.1)

де Х_і — і-та варіанта; n_i — частота і-ої варіанти.

Для інтервального варіаційного ряду середня арифметична розраховується також за формулою (1.2.1), але в ній Х_і— середина кожного інтервалу.

Медіаною називається таке значення ознаки, що вивчається, яке припадає на середину варіаційного ряду. При знаходженні медіани можливі два випадки: кількість членів ряду парна (n=2к) та непарна (n=2к+1).

Якщо всім одиницям (варіантам) дискретного ряду надати порядкові номери, то порядковий номер медіанної варіанти визначається як 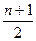 для ряду з непарною кількістю членів n.

 

Якщо ж кількість членів ряду є парним числом, то медіаною є середнє значення двох варіант, що мають порядкові номери 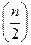 та .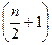

Знаходження медіани в інтервальному варіаційному ряді потребує визначення інтервалу, в якому вона знаходиться (медіанного інтервалу):

 

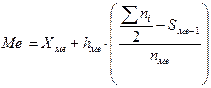,             (1.2.2)

де Ме — медіана;

Х_ме — нижня границя медіанного інтервалу;

h_ме — ширина медіанного інтервалу;

;

 

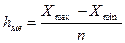де n — кількість інтервалів; n=1+3,322lgN;

N — кількість варіант;

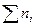— сума всіх частот (кількість членів ряду);

S_me-1 — сума частот, що накопичені до медіанного інтервалу;

n_me — частота медіанного інтервалу.

 

Модою називається варіанта, яка найчастіше зустрічається в даному варіаційному ряді. Іншими словами, для дискретного ряду мода дорівнює варіанті з найбільшою частотою.

Розрахунок моди у варіаційних рядах з рівними інтервалами здійснюється за інтерполяційною формулою:

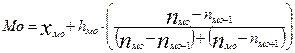,    (1.2.3)

де Мо — мода;

Х_мо — нижня границя модального інтервалу;

h_мо — ширина модального інтервалу;

n_мo-1, n_мo,n_мo+1 — частоти передмодального, модального, післямодального інтервалів, відповідно [1;3;6].

 

Приклад 2. Для варіаційного дискретного ряду з прикладу 1 розрахувати:

а) середню арифметичну;

б) медіану;

в) моду

Рішення: а) Середня арифметична:

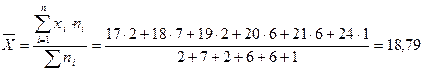 років.

 

Тобто, середній вік студентської групи 1 курсу становить 18,79 років.

б) медіана:

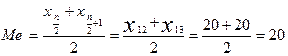 років.

в) мода:

Мо=18 років.

Мірами розсіяння варіант у варіаційних рядах є дисперсія (  ):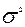

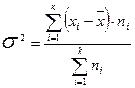,                                (1.2.4)

де х_i — i-та варіанта у дискретному ряді або середина кожного інтервалу в інтервальному ряді;

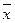— середня арифметична;

n_i — частота варіанти або інтервалу;

Середнє квадратичне відхилення ( ):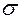

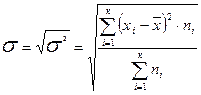;    (1.2.5)

Коефіцієнт варіації ( V ):

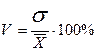.      (1.2.6)

 

Приклад 3. Для варіаційного дискретного ряду з прикладу 1 розрахувати:

а) дисперсію;

б) середнє квадратичне відхилення;

в) коефіцієнт варіації.

Рішення:

Значення варіанти, хі	Частота варіанти, ni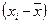
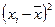
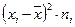
17 18 19 20 21 24	2 7 2 6 6 1	-1,79 0,79 0,21 1,21 2,21 5,21	3,204 0,624 0,044 1,464 4,884 27,144	6,408 4,369 0,088 8,785 29,305 27,144
Разом	24	Х	х	76,099

 

а) дисперсія:

;

 

 

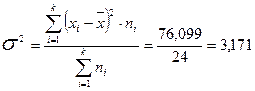б) середнє квадратичне відхилення:

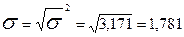 років;

 

в) коефіцієнт варіації:

.

 

Завдання 1. У випадковому порядку було відібрано 60 особистих карток студентів і виписані їх екзаменаційні оцінки з вищої математики:

4,4,2,3,5,3,5,4,3,3,4,2,4,3,5,4,4,3,3,

2,2,3,4,5,4,3,3,2,4,4,3,4,3,3,4,2,3,3,3,5,3,

3,3,4,5,2,4,3,3,3,4,4,2,3,5,4,3,5,4,3.

Побудувати варіаційний ряд розподілу студентів з успішності.

Визначити моду, медіану, середній бал, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

 

Завдання 2. У випадковому порядку було відібрано 100 клубнів картоплі та визначено вагу кожного клубня в грамах:

112, 210, 133, 215, 206, 80, 197, 134, 145, 183,251, 53, 142, 120, 177, 159, 111, 185, 200, 191, 96, 205, 138, 213, 209, 77, 201, 131, 148, 180, 260, 50, 146, 117, 180, 156, 116, 181, 203, 188, 81, 120, 135, 220, 144, 152, 150, 110, 118, 140, 125, 208, 134, 214, 209, 85, 195, 136, 143, 181, 256, 59, 142, 122, 177, 160, 114, 183, 199, 197, 101, 202, 142, 218, 209, 79, 206, 137, 148, 180, 259, 65, 82, 88, 117, 180, 68, 117, 181, 202, 188, 94, 113, 135, 220, 144, 59, 69, 100, 91.

Побудувати інтервальний ряд розподілу клубнів за вагою, утворивши при цьому 7-8 інтервалів. Для кожного інтервалу підрахувати локальні та накопичені частоти. Визначити моду, медіану середню, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

 

Завдання 3. За умовними даними середнього надою за рік від однієї корови по 20 передових господарствах регіону (дані в центнерах): 24,8; 25,9; 36,3; 41,8; 29,2; 39,6; 41,5; 51,8; 44,3; 49,5; 48,0; 36,4; 39,8; 41,6; 28,4; 49,1; 40,3; 39,6; 44,8; 53,6 побудувати варіаційний інтервальний ряд розподілу. Для кожного інтервалу ряду підрахувати локальні та накопичені частоти. Визначити моду, медіану, середню, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.

 

Завдання 4. На основі вихідних даних:

 

Групи робітників за величиною місячної заробітної плати, грн.	Кількість робітників, осіб
140 — 160 160 — 180 180 — 200 200 — 220 220 — 240	10 15 45 20 10
Разом	100

 

розрахувати показники міри рівнів (середні) та міри розсіяння.