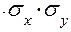Тотожність, яка пов’язує загальну суму квадратів із сумою квадратів залишків та сумою квадратів, що пояснює регресію:
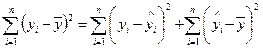 . (2.3.1)
. (2.3.1)
Кожна сума квадратів пов’язана з числом, яке називають її “ступенем вільності”. Це число показує, скільки незалежних елементів інформації, що утворилися з елементів 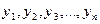 , потрібно для розрахунку даної суми квадратів.
, потрібно для розрахунку даної суми квадратів.
У статистиці кількістю ступенів вільності певної величини часто називають різницю між кількістю різних дослідів і кількістю констант, установлених в результаті цих дослідів незалежно один від одного.
Суми квадратів пов’язані з певним джерелом варіації, а також із ступенями вільності і середніми квадратами. Зведемо їх у таблиці, яка називається базовою таблицею дисперсійного аналізу ( ANOVA — таблиця). [5]
ANOVA -таблиця
| Джерело варіації
| Кількість ступенів вільності
| Сума квадратів
| Середні квадрати
|
| Зумовлене регресією (модель)
|
1
| 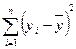
| 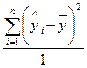
|
| Непояснюване за допомогою регресії (помилка)
|
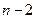
| 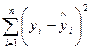
| 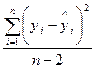
|
| Загальне
|
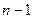
| 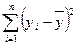
|
Не розраховується
|
Приклад 3. За даними та результатами прикладу 1 побудувати ANOVA-таблицю дисперсійного аналізу.
Рішення: Попередні розрахунки представимо в таблиці.
| i
| 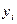
| 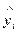
| 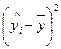
| 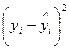
| 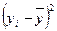
|
| 1
2
3
4
5
| 25
30
35
45
65
| 25
28
37
46
64
| 225
144
9
36
576
| 0
4
4
1
1
| 225
100
25
25
625
|
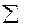
|
200
|
200
|
990
|
10
|
1000
|
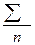
|
40
|
40
|
x
|
x
|
x
|
Побудуємо ANOVA-таблицю для прикладу про залежність між обсягами реалізації продукції та витратами на рекламу.
| Джерело варіації
| Кількість ступенів вільності
| Сума квадратів
| Середні квадрати
|
| Модель
| 1
| 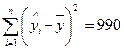
| 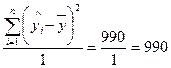
|
| Помилка
| n-2=5-2=3
| 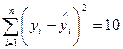
| 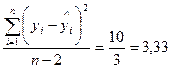
|
| Загальне
| n-1=5-1=4
| 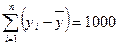
|
Не розраховується
|
Перевірка простої регресійної моделі на адекватність.
Поняття F -критерію Фішера
Критерій, що однозначно відповідає на питання про адекватність побудованої регресійної моделі — F -критерій Фішера:
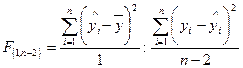 , (2.4.1)
, (2.4.1)
де чисельник — середній квадрат, який можна пояснити з регресійної моделі;
знаменник — середній квадрат помилок;
1, (n-2) — ступені вільності.
Перевірка моделі на адекватність за F-критерієм Фішера передбачає здійснення певних етапів:
1. На першому етапі розраховуємо величину F-критерію Фішера за формулою (2.4.1).
2. На другому етапі задаємо рівень значимості 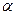 або
або 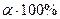 . Наприклад, якщо ми вважаємо, що можлива помилка
. Наприклад, якщо ми вважаємо, що можлива помилка 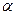 для нас становить 0,05 (або 5%), це означає, що ми можемо помилитися не більше, ніж у 5% випадків, а в 95% випадків
для нас становить 0,05 (або 5%), це означає, що ми можемо помилитися не більше, ніж у 5% випадків, а в 95% випадків 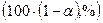 наші висновки будуть правильними.
наші висновки будуть правильними.
3. На третьому етапі за статистичними таблицями F-розподілу Фішера з (1, n-2) — ступенями вільності і рівнем довіри 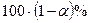 обчислимо критичне значення (Fкр.).
обчислимо критичне значення (Fкр.).
4. Якщо розраховане нами значення F>Fкр. , то з ризиком помилитися не більше, ніж у 5% випадків, ми можемо вважати, що побудована регресійна модель адекватна реальній дійсності [5].
Приклад 4. Перевірити на адекватність лінійну регресійну модель, побудовану в прикладі 1, за критерієм Фішера.
Рішення: Використовуючи ANOVA-таблицю дисперсійного аналізу, побудовану в прикладі 3, розрахуємо F-критерій Фішера за формулою (2.4.1):
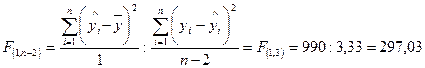
За таблицею F-розподілу Фішера знаходимо критичне значення (Fкр) з 1 та 3 ступенями вільності, задавши попередньо рівень довіри 95% або рівень значимості (помилки) 5%. Це буде точка:
F(1;3;0,95)=10,13.
Отже, F>Fкр., тобто, 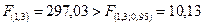 , що дозволяє зробити висновок про адекватність побудованої моделі реальній дійсності.
, що дозволяє зробити висновок про адекватність побудованої моделі реальній дійсності.
Завдання 12. За даними завдання 4 побудувати ANOVA-таблицю дисперсійного аналізу та перевірити на адекватність лінійну регресійну модель, одержану при виконанні завдання 4, за допомогою F-критерія Фішера.
Завдання 13. За даними завдання 8 побудувати ANOVA-таблицю дисперсійного аналізу та перевірити на адекватність лінійну регресійну модель, одержану при виконанні завдання 8, за допомогою F-критерія Фішера.
Завдання 14. За даними завдання 10 побудувати ANOVA-таблицю дисперсійного аналізу та перевірити на адекватність лінійну регресійну модель, одержану при виконанні завдання 10, за допомогою F-критерія Фішера.
Завдання 15. За даними завдання 11 побудувати ANOVA-таблицю дисперсійного аналізу та перевірити на адекватність лінійну регресійну модель, одержану при виконанні завдання 11, за допомогою F-критерія Фішера.
Завдання 16. Припустимо, що в регресії 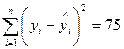 та
та 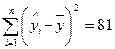 . Використайте F-критерій Фішера для перевірки значимості регресії (n=30). Використовуйте 5%-ий
. Використайте F-критерій Фішера для перевірки значимості регресії (n=30). Використовуйте 5%-ий
рівень значимості.
Тест
Вибрати правильну відповідь на запитання:
1. Лінійна регресія:
а) лінія, що відображає зв’язок між незалежною і залежною змінними;
б) інша назва простої регресії;
в) лінія, яка завжди має нахил, що дорівнює 1;
г) графік значень незалежної і залежної змінних;
д) лінія, яка завжди має нахил, що дорівнює 0
.
2. Нахил:
а) точка, де лінія регресії перетинає вісь у;
б) вимірює придатність лінії регресії;
в) вимірює зв’язок між залежною і незалежною змінними;
г) завжди дорівнює 1;
д) інша назва коефіцієнта детермінації
.
3. Перетин:
а) точка, де лінія регресії перетинає вісь у;
б) вимірює придатність лінії регресії;
в) вимірює зв’язок між залежною і незалежною змінними;
г) завжди дорівнює 1;
д) завжди дорівнює 0
.
4. Що з наведеного не є припущенням моделі лінійної регресії:
а) або 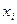 є сталими числами, або вони є статистично-незалежними від випадкових величин
є сталими числами, або вони є статистично-незалежними від випадкових величин 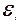 ;
;
б) дисперсія випадкової величини 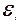 є сталою;
є сталою;
в) математичне сподівання випадкової величини 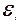 дорівнює нулеві;
дорівнює нулеві;
г) дисперсія випадкової величини дорівнює 0;
д) випадкові величини є статистично незалежними одна від одної
.
5. Коефіцієнт детермінації:
а) точка, де лінія регресії перетинає вісь у;
б) вимірює придатність лінії регресії;
в) вимірює зв’язок між незалежною і залежною змінними;
г) завжди дорівнює 1;
д) завжди дорівнює 0
.
6. Коефіцієнт детермінації вимірює:
а) варіацію незалежної змінної;
б) нахил лінії регресії;
в) перетин лінії регресії;
г) загальну варіацію залежної змінної, що пояснюється регресією;
д) завжди дорівнює 1
.
7. Сума квадратів, що пояснює регресію:
а) 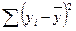 ;
;
б) 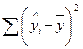 ;
;
в) 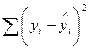 ;
;
г) 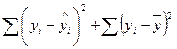 ;
;
д) 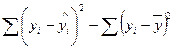 .
.
8. Сума квадратів помилок:
а) 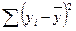 ;
;
б) 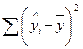 ;
;
в) 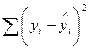 ;
;
г) 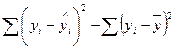 ;
;
д) 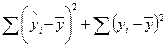
9. Коваріація між х та у є:
а) 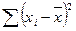 ;
;
б) 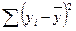 ;
;
в) 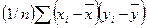 ;
;
г) r yx 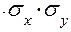
д) в і г.
10. Якщо ми хочемо, використовуючи регресійний аналіз, виміряти зв’язок між досвідом роботи і заробітною платою, то:
а) незалежною змінною має бути заробітна плата;
б) незалежною змінною має бути досвід роботи;
в) залежною змінною має бути заробітна плата;
г) залежною змінною має бути досвід роботи;
д) б і в
.
11. У регресії: у=0,34+1,2х нахил дорівнює:
а) х;
б) у;
в) 0,34;
г) 1,2;
д) 1,2/0,34.
12. У регресії: у=0,34+1,2х перетин дорівнює:
а) х;
б) у;
в) 0,34;
г) 1,2;
д) 1,2/0,34.
13. З урахуванням співвідношення між заробітною платою (в гривнях) —у і освітою (в роках) —х, у=12,201+525х, особа, яка навчалася додатково один рік, може очікувати на таку додаткову оплату:
а) 12,201;
б) 525;
в) 24,402;
г) 1,050
д) 12,201+525.
14. З урахуванням співвідношення між заробітною платою (в гривнях) — у і освітою (в роках) — х, у=12,201+525х, особа, що навчалася додатково нуль років, може очікувати на таку додаткову оплату:
а) 12,201;
б) 525;
в) 24,402;
г) 1,050;
д) 12,201+525.
15. Якщо регресія має R2=0,80, то регресійна лінія:
а) пояснює 80% варіації змінної х;
б) пояснює 80% варіації змінної у;
в) матиме нахил 0,80;
г) матиме перетин 0,80;
д) не пояснює зв’язку між х і у.





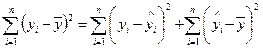 . (2.3.1)
. (2.3.1)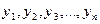 , потрібно для розрахунку даної суми квадратів.
, потрібно для розрахунку даної суми квадратів.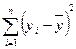
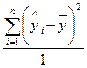
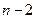
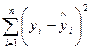
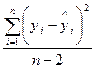
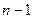
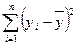
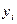
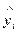
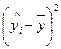
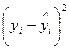
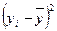
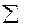
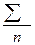
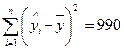
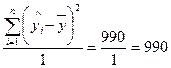
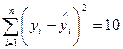
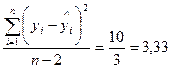
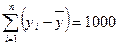
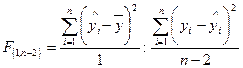 , (2.4.1)
, (2.4.1)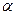 або
або 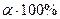 . Наприклад, якщо ми вважаємо, що можлива помилка
. Наприклад, якщо ми вважаємо, що можлива помилка 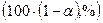 наші висновки будуть правильними.
наші висновки будуть правильними.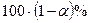 обчислимо критичне значення (Fкр.).
обчислимо критичне значення (Fкр.).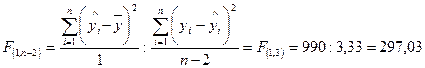
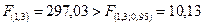 , що дозволяє зробити висновок про адекватність побудованої моделі реальній дійсності.
, що дозволяє зробити висновок про адекватність побудованої моделі реальній дійсності.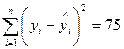 та
та 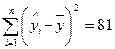 . Використайте F-критерій Фішера для перевірки значимості регресії (n=30). Використовуйте 5%-ий
. Використайте F-критерій Фішера для перевірки значимості регресії (n=30). Використовуйте 5%-ий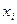 є сталими числами, або вони є статистично-незалежними від випадкових величин
є сталими числами, або вони є статистично-незалежними від випадкових величин 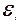 ;
;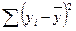 ;
;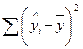 ;
;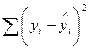 ;
;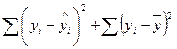 ;
;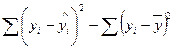 .
.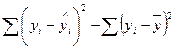 ;
;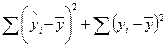
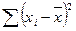 ;
;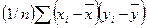 ;
;