Теорія комплексних чисел як упорядкованих пар дійсних чисел.

Розглянемо множину впорядкованих пар 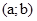, де a і b – дійсні числа. Дві пари 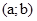і 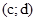 вважаться рівними, якщо  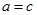і , і 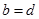записують .

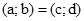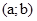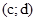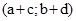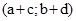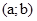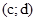Сумою пар і  називають пару . Кажуть, що пару  дістали внаслідок додавання пар і  і записують .

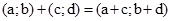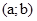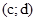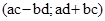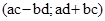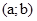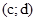Добутком пар і  називають пару . Кажуть, що пару дістали внаслідок множення пар і  і записують .

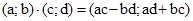Нульовою парою називають пару 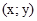, яка задовольняє умову 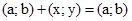, де 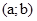 - довільна пара. З означення операції додавання і рівності пар, випливає, що пара  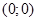- нульова.

Одиничною парою називають пару 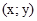, яка задовольняє умову 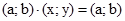, де 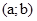 - довільна пара. З означення операції множення і рівності пар, випливає, що пара  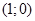- одинична.

У множині впорядкованих пар операції додавання і множення пар мають обернені операції – віднімання і ділення. Різницю і частку пар 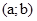і 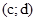 обчислюють відповідно за формулами: ,

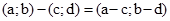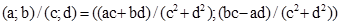 (для частки вважається, що пара  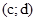- не нульова).

Ототожнюють пару вигляду 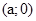 з дійсним числом а. Неважко перевірити, що при такому ототожнені сумою і добутком пар  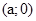і 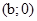 є пари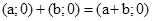 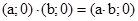, які за прийнятою умовою ототожнюються з числами  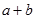і 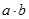 відповідно.

Аналогічно можна показати, що різниця і частка пар 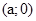 і 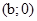 - пари з нульовими другими елементами, тобто дійсні числа (для частки вважається, що ).

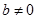Візьмемо тепер пару 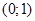 і за правилом множення пар помножимо її саму на себе:  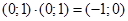 (6) в результаті множення дістали пару 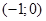, яка відповідає дійсному числу -1. Ввівши для пари  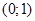спеціальне позначення 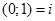, рівність (6) можна записати у вигляді  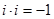 або .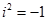

Проста перевірка показує, що будь – яку пару дійсних чисел 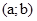 можна записати у вигляді  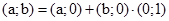або за прийнятою умовою про ототожнення множини всіх пар  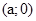і множини всіх дійсних чисел а і прийнятого позначення для пари 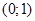, у вигляді 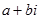.      (7)

Введено операції додавання і множення впорядкованих пар дійсних чисел і показано, що будь – яке комплексне число можна записати у вигляді комбінації впорядкованих пар дійсних чисел (7).