Сейчас мы рассмотрим, какие результаты покажут различные формулы ЭД в вычислительных экспериментах при распространении условного сигнала в пространстве между источником и приёмником без учёта аберрационных поправок, возникающих в самих источнике и приёмнике, т.е. при их мембранной конструкции. Вычислительные эксперименты будем проводить на математических моделях классического и релятивистского ЭД как при движении сигнала в математической пустоте, так и в реальной среде с различной оптической плотностью и использовать для этого будем мою программу Dopler6. К сожалению, после публикации 1-ой редакции статьи я понял, что многие до сих пор имеют смутное представление о том, что такое математическая модель и что такое вычислительный эксперимент (наверное, этот термин введен мною впервые), поэтому возникло много вопросов о приведенных мною "наблюдательных" данных, полученных при проведении вычислительного эксперимента. В связи с этим я решил прямо в этой статье устроить маленький ликбез по этим вопросам, изложив вкратце материал своих работ [14, 15] по моделям и имитаторам и немного коснуться вопроса о вычислительном эксперименте (см. Приложение 2). А сейчас мы начнем с рассмотрения классического ЭД в математической пустоте (тоже самое будет и в какой то среде с неизменными свойствами этой среды, когда она неподвижна), где для его описания у нас получилась очень простая математическая модель.
Здесь моделируемая нами система, т.е. СТ, состоит из источника, приемника и предаваемого сигнала, поэтому уравнений описывающих функционирование этой системы получилось не много и к тому же здесь рассматривается прямолинейное равномерное движение источника и приемника, что значительно упрощает описание. Сами уравнения этой математической модели я привожу ниже, но можете посмотреть их и в исходниках программы Dopler6 - это файл form1.frm (можно просмотреть обычным Блокнотом в конце файла, т.к. код начинается после описания самой формы, которое дано в начале файла). Мы при проведении вычислительных экспериментов на этой модели будем решать систему уравнений, приведенную ниже, численными методами, т.е. с использованием множества мелких итераций с шагом решения по времени P0. А, кого интересует решение этой системы уравнений аналитически поэтапно, т.е. когда мы не получаем как при аналитическом решение системы уравнений сразу окончательный ответ (например, смотрите нижеприведенную формулу (10*)), а решаем систему уравнений аналитически, но для каждого отдельного этапа с нахождением различных показателей ее функционирования на этом этапе и последующего расчета по ним самого эффекта, могут ознакомиться с этим решением в Приложении 1.
X1=X1+VX1*P0
Y1= Y1+VY1*P0
X2=X2+VX2*P0
Y2= Y2+VY2*P0
R=((X1-X2n)^2+(Y1-Y2n)^2)^0,5
Rs=Rs+Vs*P0
T=T+P0
где X1, Y1, X2, Y2 - текущие координаты, соответственно, приемника и источника.
X2n, Y2n - координаты источника в момент времени, когда сигнал о начале или конце периода колебаний был излучен передатчиком расположенном на источнике.
VX1, VY1, VX2, VY2 - скорости приемника и источника по осям координат.
Rs и R - соответственно радиус сферы, до которой распространился фронт сигнала от источника с момента его излучения до текущего момента времени, и расстояние между текущим положением приемника и положением источника в тот момент времени, когда сигнал о начале или конце периода колебаний был излучен передатчиком.
Vs - скорость распространения сигнала в математической пустоте или в какой-то среде с постоянными свойствами.
T - текущее время, P0 - шаг интегрирования (шаг решения уравнений).
Многие, посмотрев на эти уравнения, сильно удивятся и зададутся вопросом, неужели это и есть математическая модель ЭД? Да, это самая что ни на есть настоящая математическая динамическая модель классического ЭД. А вот все теоретические формулы, которые мы рассмотрели ранее (2, 3-1, 3-2, 4-1...4-6), являются математическими имитаторами (симуляторами или, если хотите, симулянтами) этого эффекта, и таких имитаторов может быть много (хотя, кстати, и моделей для сложных систем тоже может быть несколько). Причём эти имитаторы иногда бывают окончательным решением (пусть и с какими-то допущениями) системы уравнений, являющейся математической моделью системы, но чаще всего это просто аппроксимация какими-то уравнениями экспериментальных данных в определённых условиях, хотя иногда такая аппроксимация и выглядит отражением логических закономерностей процессов, описанных ею - именно такими имитаторами и являются все рассмотренные нами формулы ЭД, в которых почти все видят больше, чем простые аппроксимации, и пытаются найти там какой-то глубинный смысл. Хотя эти имитаторы являются просто расчётными формулами, которые упрощают процесс вычислений при рассмотрении ЭД. Хотя надо заметить, что точные аналитические решения уравнений математической модели действительно позволяют нам понять рассматриваемое явление с какой-то точки зрения, но это бывает очень редко, т.к. почти все окружающие нас системы описываются нелинейными дифференциальными уравнениями, а последние аналитически не решаются, и остаётся только численно решать системы таких уравнений, по результатам чего делать потом какие-то определённые логические выводы некорректно.
По различным расчётным формулам ЭД мы можем определить только мгновенную частоту принимаемого сигнала в конкретных положениях приемника, чего в реальности быть не может. Ведь в реальности мы можем зафиксировать прибором частоту принимаемых сигналов только в том случае, если мы примем хотя бы один полный период колебаний, а за это время и источник и приемник немного изменят свое положение, т.е. изменится угол наблюдения, а возможно, что и скорости, и поэтому нельзя сказать определенно какому положению источника и приемника соответствует эта частота. Поэтому, для сравнения наблюдаемых и расчетных данных, мы будем находить наблюдаемую частоту по времени приема одного периода колебаний при моделировании ЭД, а расчетную частоту (по нашим имитаторам, т.е. различным формулам ЭД) в начале приема периода и в конце по получающимся при моделировании параметрам в эти моменты времени. А потом будем находить среднее расчетное значение частоты для этого периода и сравнивать его с наблюдаемым значением частоты, полученным по его наблюдаемому в эксперименте периоду, т.е. по разности времени прихода двух фронтов сигнала на приемник, излученных в моменты начала и конца одного периода колебаний на источнике. Хотя, можно было бы определять и по расчетным формулам сразу среднюю частоту приема сигнала, но для этого надо было бы в расчетных формулах использовать все углы Q для положения источника и приемника в середине принимаемого периода.
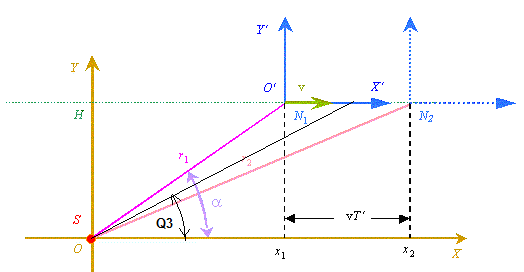
Рис. 18. Схема к расчету периода принимаемого сигнала для общего ЭД при неподвижном источнике (воспроизведено из работы [12]).
Например, если бы у нас источник был неподвижен в точке O, а приемник двигался со скоростью V, то это было бы положение между точками N1 и N2 для угла наблюдения Q3, как это показано на рис. 18. Но я считаю, что это бы только запутало расчеты, поэтому мы будем вычислять по различным формулам ЭД две принимаемые частоты (в начале и в конце расчетного периода, т.е. в положениях приемника N1 и N2), а потом находить среднюю частоту для среднего угла наблюдения. Вообще то, можно было бы и не проводить вычислительный эксперимент на модели системы, где движутся по заданным уравнениям источник, приемник и сигнал, а решить аналитически эту систему уравнений и получить точную формулу для наблюдаемой частоты принимаемого сигнала, т.е. именно формулу для ЭД, но в виде имитатора, т.е. в том виде, как мы привыкли вычислять ЭД. При этом решении саму частоту приема мы определили бы так же по периоду времени между двумя моментами времени прихода сигнала о начале периода и его конце к приемнику, но я считаю, что и это еще больше запутало бы рассмотрение этого вопроса и к тому же мы бы лишились наглядности этого процесса, который при проведении вычислительного эксперимента в программе Dopler6 мною еще и анимирован.
Да и аналитическая формула получилась бы слишком громоздкой, т.к., например, в работе [12] такая формула (10*), которую я привожу ниже, уже для частного случая движения только приемника и только по одной оси координат получилась очень сложной (к тому же, в расчете используется только один угол, что является ошибкой). А для общего случая, т.е. и при движении источника и при движениях источника и приемника по двум осям координат и при расчете по двум углам, т.е. в начале и конце периода колебаний на источнике, она будет на порядок или на два больше, т.е. на целую страницу, и это лишит нас простоты и наглядности, которую дает вычислительный эксперимент. Кстати, авторы [12] пренебрегли тем обстоятельством, что мы вычисляем наблюдаемую частоту по периоду времени между двумя точками приема начала и конца одного периода сигнала, т.е. примерно для угла Q3, и поэтому, используя данные, полученные ими по формуле (10*), которую они выводили по рис. 18 с использованием угла α, т.е. угла наблюдения в начале приема периода колебания, они пришли к выводу о том, что при классическом рассмотрении этого вопроса тоже будет поперечный ЭД.
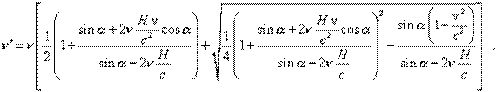 (10*)
(10*)
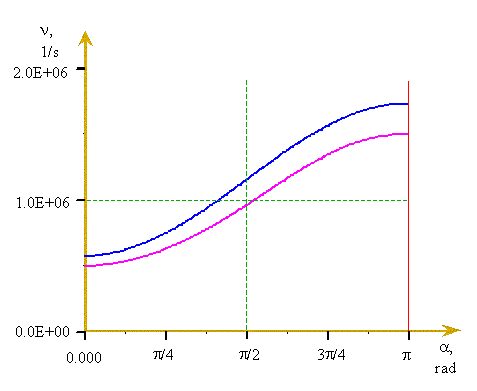
Рис. 19. Графики зависимости относительного изменения частоты, принимаемой движущимся наблюдателем при неподвижном источнике в общем ЭД в функции от изменения угла α. Синяя кривая по СТО, сиреневая - классика (воспроизведено из работы [12]).
Но если они устранят эту ошибку и будут определять на рис. 18 угол α не в направлении на точку N1, а в направлении на середину отрезка между точками N1 и N2, то на рис. 19 у них в той точке графика, где у них указан угол pi/2, получится угол немного меньше, а угол α будет равен именно pi/2 немного правее. Таким образом, их график на рис. 19 пройдет в точке pi/2 ровно через значение частоты передатчика отложенной по вертикальной шкале и никакого поперечного ЭД не будет. Кстати, для тех, кто заинтересуется этой работой, отмечу особо, что ни только никаких вычислений по формуле для общего ЭД (2) они в этой работе не производят, но они вообще этой формулы не приводят в своей работе. Это я к тому, чтобы, ознакомившись с этой работой, некоторые читатели не подумали, что у них поперечный ЭД получился не из-за методологической ошибки определения наблюдаемой частоты приема при классическом расчёте, а именно, из классической формулы (2). А у меня при проведении вычислительных экспериментов на классической математической модели ЭД никакого поперечного ЭД не наблюдается. Для этого рассмотрим движение источника и приемника, а также распространение фронтов волн (генерируемых передатчиком с заданной частотой v0) в пространстве между источником и приемником, как это изображено на рис. 20, где вычислительный эксперимент выполняется на математической модели классического ЭД описанной выше.
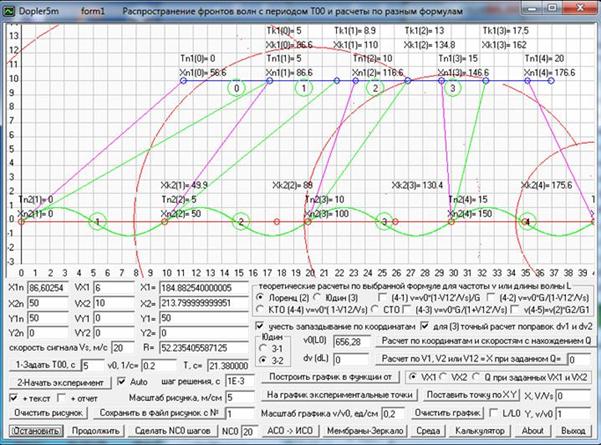
Рис. 20. Вычислительный эксперимент по распространению волн от движущегося на нулевой высоте со скоростью 10 м/с источника 2 и принимаемых движущимся на высоте 50 м со скоростью 6 м/с приемником 1. В зеленых кружках между двумя положениями источника и приемника указаны номера условных периодов между моментами времени, когда передатчик сделал одно колебание и приемник принял сигналы начала и конца этого колебания. Скриншот программы Dopler5m.
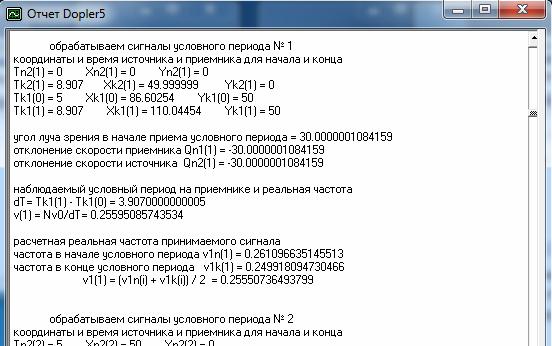
Рис. 21. Отчет по вычислительному эксперименту на рис. 20. Скриншот программы Dopler5m.
Конкретно, здесь v0=0,2 Гц и один период колебаний T00= 5 с, который используется в расчётах для начала движения сигнала в начале каждого нового периода колебаний передатчика. В тот момент времени, когда этот сигнал достигает движущегося приемника, мы фиксируем время его прихода и потом находим промежутки времени между этими соседними зафиксированными моментами времени прихода сигнала, т.е. определяем наблюдаемый период принимаемого сигнала. И ниже в табл. 6, как наблюдения, я и привожу данные вычислительного эксперимента, взятые из отчета о работе программы при исходных данных заданных на форме 1 программы. Здесь мы видим, что на приемнике первый период был принят между моментами времени 5 с и 8,907 с, т.е. период был равен 3,907 с. Следовательно, на этом промежутке времени средняя частота принимаемого сигнала была 0,256 Гц, а, если мы по формуле (2) рассчитаем мгновенную частоту приема в начале и в конце этого периода, то мы получим 0,261 и 0,250 Гц, что даст среднюю частоту для этого периода опять таки 0,256 Гц.
Табл. 6. Наблюдаемые и расчетные данные частоты принимаемого сигнала при распространении сигнала с частотой передатчика 0,2 Гц для семи периодов сигнала (форма 1).
| № периода
| 1
| 2
| 3
| 4
| 5
| 6
| 7
|
| наблюдения
| 0,256
| 0,242
| 0,221
| 0,202
| 0,189
| 0,182
| 0,179
|
| формула (2)
| 0,256
| 0,241
| 0,221
| 0,202
| 0,189
| 0,183
| 0,179
|
Тут мы видим отличное совпадение наблюдаемых данных с рассчитанными по формуле (2), хотя и имеется маленькое расхождение, но это объясняется не ошибками в формуле (2) или в коде программы, а погрешностью определения среднего угла наблюдения и численным решением уравнений. И чем больше у нас будет расстояние между двумя углам наблюдения, пройденное приемником за один расчетный период, тем больше будет эта погрешность на графике, построенном в функции от средних углов наблюдения для рассчитываемого периода приема сигнала. Хотя, как это видно на рис. 22, для нашего примера формула (2) очень даже точно отражает результаты вычислительного эксперимента во всем диапазоне углов наблюдения. А для реальных частот излучения, которые есть у звука или света, и обычно наблюдаемых скоростях источника и приемника эта разность в двух углах наблюдения для одного периода будет очень не большой и при построении графиков вообще не будет наблюдаться никакого несоответствия наблюдаемых и расчетных данных. К сожалению у нас почти все точки в этом вычислительном эксперименте получились вблизи угла наблюдения 90 градусов, поэтому, чтобы получилась хорошая экспериментальная кривая, давайте дополним их экспериментальными данными при других начальных координатах приемника и источника (Y1n=20 м и X2n=40м). Для этого выведем полученные экспериментальные данные в первом вычислительном эксперименте на график и выполним второй вычислительный эксперимент, а, чтобы при этом анимация не затеняла график увеличим масштаб рисунка до 20 м/см и отключим вывод текста на рисунок. А после выполнения и этого вычислительного эксперимента тоже выведем данные на график, как это показано на рис. 22, где мы видим, что расчётная кривая по формуле (2) хорошо аппроксимирует данные наблюдений во всем диапазоне углов наблюдения (от 14 до 157 градусов).
Но экспериментальные данные, полученные на этой форме 1, будут соответствовать только теоретическим данным по формуле (2), а релятивистские формулы будут неправильно отражать результаты вычислительного эксперимента, т.к. в данном случае мы моделировали ЭД без учета изменения темпа течения времени на приёмнике и источнике. Естественно, и мои формулы (3-1) или (3-2) тоже будут неправильно отражать эти наблюдаемые данные, т.к. в применявшейся нами математической модели ЭД на этой форме 1 не закладывались и аберрационные эффекты.
Поэтому в программе есть и другие формы, где использовавшиеся там математические модели позволяют рассмотреть и другие варианты ЭД. При этом данные наблюдений хорошо аппроксимируются формулой (2) только в том случае, если мы их определяем для углов наблюдения, полученных с использованием запаздывающих координат источника (на рис. 20 эти углы отражают зелёные прямые), а если мы для расчёта углов наблюдения используем синие прямые, которые соединяют текущие координаты источника и приёмника в начале каждого условного периода, то выведенные на график на рис. 22 экспериментальные данные (красные кружки) не аппроксимируются формулой (2). Это наглядно показывает, что в формулах ЭД всегда надо использовать запаздывающие координаты источника.
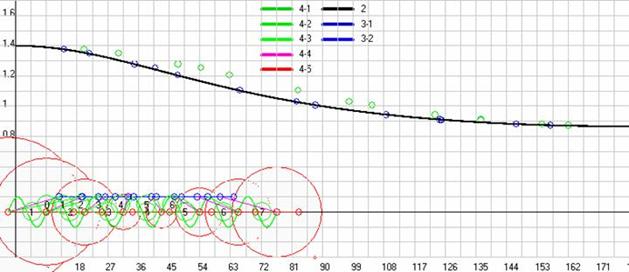
Рис. 22. Сравнение наблюдаемых данных (частоты принимаемого сигнала) вычислительного эксперимента (кружки) и расчетных значений полученных по формуле (2) (черная кривая) в функции угла наблюдения, полученных при движении приемника в двух экспериментах на высоте 50 и 20 м со скоростью 6 м/с, а передатчика на нулевой высоте со скоростью 10 м/с. Синие кружки при использовании в расчетах и для графика по оси Х углов наблюдения полученных по запаздывающим координатам источника, а красные кружки по текущим координатам. Скриншот программы Dopler5m.
А теперь давайте рассмотрим некоторые случаи излучения и поглощения плоских волн, где у нас в зависимости от ориентации мембран источника и приемника возможны различные варианты проявления ЭД. При этом рассмотрим только вариант с приемником, т.к. на источнике будут происходить аналогичные процессы. Простейшим примером для приемника является случай изображенный на рис. 23 в варианте 1, где у нас мембрана перпендикулярна и скорости сигнала Vs и скорости приемника V1. В учебниках этот случай называют продольным ЭД. А в варианте 2 у нас мембрана перпендикулярна скорости сигнала, но параллельна скорости приемника и в учебниках этот случай называют поперечным ЭД. Но, здесь возможен еще один вариант 3, когда у нас мембрана перпендикулярна скорости приемника, но параллельна скорости сигнала. А вот в этом случае у нас не будет вообще никакого эффекта, хотя с формальной точки зрения, т.е. так, как это дается в учебниках без учета конструкции приемника, мы тоже должны наблюдать поперечный ЭД. А теперь давайте рассмотрим общий случай ЭД, т.е. когда у нас скорости сигнала и приемника расположены под произвольным углом наблюдения Q1 и когда у нас при покоящемся источнике будет укороченная формула (2) v =v0*(1 – b1*cos(Q1)) .
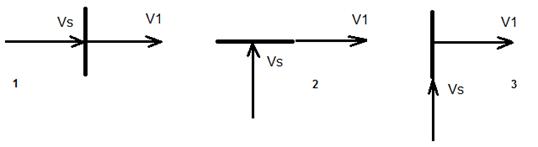
Рис. 23. Возможные варианты ЭД при различном положении плоскости мембраны приемника относительно скоростей сигнала и приемника.
Для этого сначала рассмотрим случай отражения плоской волны от движущегося зеркала. Пусть у нас мембрана приемника расположена под произвольным углом А0 к скорости приемника V1 и к ней приближается со скоростью Vs фронт плоской волны, который в данный момент коснулся своим правым краем мембраны приемника в точке 1, как это показано на левом рис. 24. Но, пока левый край фронта волны долетит до мембраны, она немного переместится вправо и он коснется мембраны в точке 2. Отраженный фронт волны будет теперь распространяться так, что его левый и правый края начнут движение из точек 1 и 2. Следовательно, отраженный фронт волны будет теперь двигаться не под углом отражения равном углу падения к плоскости мембраны, а под углом отражения равном углу падения к эффективной плоскости мембраны, т.е. к плоскости между точками 1 и 2. А воспользовавшись формой 8 программы Dopler6 Вы можете поэкспериментировать с различными скоростями приемника и углом наклона его мембраны, чтобы посмотреть как при этом будет изменяться эффективный угол отражения. Один из вариантов такого расчета представлен на правом рисунке 24.
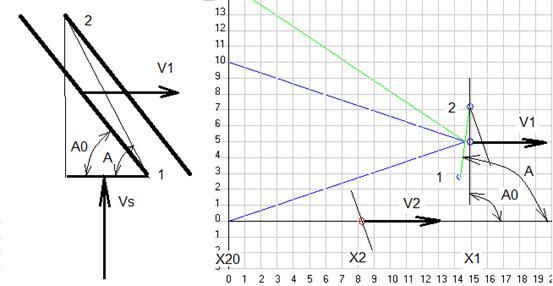
Рис. 24. Схема для расчёта эффективного угла наклона мембраны при её движении (слева) и скриншот программы Dopler5m с одним из примеров расчёта этого угла (справа).
Я понимаю, что для некоторых читателей такой вывод об изменение угла отражения не совсем очевиден, но он подтверждается не только теоретически, но и экспериментально [44]. Не знаю, может быть, это будет более понятно, если мы рассмотрим свет как движение корпускул - давайте попробуем это сделать. Для этого воспользуемся моей программой Udar3m, где зададим массу корпускулы m1=1 кг, а массу стержня очень большой m2=9*10^7 кг (у нас это будет мембрана), чтобы корпускула не сильно изменила скорость стержня после удара. При этом корпускулу будем считать абсолютно упругой с жесткостью 4*10^6 н/м, а ее начальные скорости зададим VX1=30 м/с и VY1=17,32 м/с, что даст суммарную скорость V1=34,64 м/с. В первом вычислительном эксперименте у нас мембрана будет неподвижна (левый рисунок 25), а во втором (правый рисунок 25) зададим ей скорость VX2=10 м/с (здесь VX2 и VX1 это не скорости источника и приемника, т.к. в программе Udar3m индексация другая). У нас получится в первом эксперименте угол отражения равный углу падения, т.е. 30 градусов (измеряется от нормали к плоскости мембраны), что не вызывает вопросов, а вот во втором эксперименте у нас получится угол отражения 60 градусов, т.е. изменился эффективный угол наклона мембраны, но я думаю, что и это тоже будет многим не очень понятно. Тем более, что у нас после отражения скорость корпускулы по оси Y так и осталась 17,32 м/с, а вот по оси X стала -10 м/с (при этом скорость VX2 стала 10,0000044 м/с), хотя программа показывает, что при этом и закон сохранения энергии и закон сохранения количества движения полностью были соблюдены. Могу только, как подсказку, привести общеизвестный пример с поездом, который на скорости 10 м/с врезается в дрезину, стоящую на путях, и та отскакивает со скоростью 20 м/с, а не 10, как некоторые могли подумать.

Рис. 25. Анимация процесса удара корпускулы (красный круг) в массивную мембрану при моделировании этого процесса в программе Udar3m. Левый рисунок - мембрана покоится, а правый рисунок - движется горизонтально.
Ну, а если и после этого пояснения не всё стало понятно, то это несмертельно, т.к. при рассмотрение самого ЭД нас не очень-то интересуют углы наклона мембран, т.к. на частоте принятого сигнала они никак не отразятся. Эти углы будут нас интересовать только в том случае, если мы будем рассчитывать и направление сигнала отраженного от движущихся зеркал, например, в эксперименте Майкельсона-Морли. А, чтобы понять почему углы наклона мембран не отразятся на частоте принятого сигнала давайте обратимся к рисунку 26, где у нас источник, покоящийся в начале системы координат, излучает в общем случае сферические волны, но мы рассматриваем только движение маленького участка фронтов этих волн, которые считаем на этом маленьком участке плоскими и рассматриваем встречу двух фронтов этих плоских волн с мембраной движущегося приемника.
Сначала рассмотрим случай, когда плоскость фронта волны всегда параллельна плоскости мембраны приемника, что изображено на левом рис. 26. В этом случае у нас и левый 2, и правый 1 края фронта волны коснутся одновременно плоскости мембраны приемника, движущегося со скоростью V1, т.е. время прихода фронта и 1-ой и 2-ой волны определяется однозначно, и мы легко вычислим как наблюдаемый период принятого сигнала, так и его частоту. А если у нас мембрана приемника будет расположена всё время вертикально, как показано на правом рис. 26, то у нас в вычислительном эксперименте будет зарегистрировано по два значения времени прихода фронта волны к приемнику (в точках 1 и 2), если считать, что между этими моментами времени мембрана приёмника была неподвижной. И как не трудно заметить, среднее время прихода волны в этом случае будет в тот момент, когда средняя часть фронта волны пройдет мембрану приемника, т.е. это будет то же самое время, какое мы зафиксировали на левом рисунке. А если мембрана будет двигаться и между моментами времени касания её двумя краями фронта волны, то эти точки 1 и 2 будут просто симметрично расположены чуть левее и чуть правее, что всё равно приведет к тому, что средняя часть фронта волны коснётся мембраны приёмника в той же средней точке.
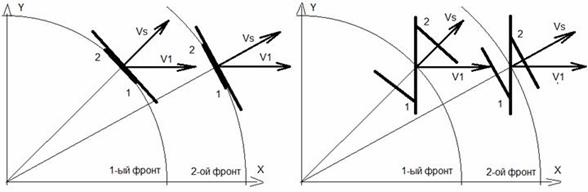
Рис. 26. Схема к расчету момента приема фронта плоской волны мембраной приемника. Правый рисунок - мембрана расположена вертикально, а левый рисунок - по касательной к сферическому фронту волны.
Таким образом, получается, что при любом угле наклона мембраны приемника у нас в вычислительном эксперименте время прихода на приёмник очередного фронта волны будет то же самое, т.е. угол наклона мембраны приемника никак не влияет на частоту принятого сигнала, т.е. никак не должен быть отражен и в формуле ЭД. При этом мы можем считать, что реальный маленький участок каждого фронта волны будет принят на приёмнике в момент времени, когда его средняя часть пересечётся со средней частью мембраны приемника, но можем и вычислить этот момент по двум моментам времени, когда правый и левый края фронта волны коснулись мембраны приемника и возможность выполнения такого условия у меня предусмотрена в математической модели реализованной на форме 8 программы. Для этого перед началом вычислительного эксперимента надо отметить чекбокс <+ изменять A2>, т.е. изменять угол наклона мембраны источника для создания очередного фронта плоской волны в начале каждого периода колебаний передатчика так, чтобы, когда фронт достигнет приемника, то центр фронта совпадал с центром мембраны приемника. А если мы отметим ещё и чекбокс <++ изменять А1=A2>, то у нас при проведение вычислительного эксперимента будет изменяться и угол наклона мембраны приёмника так, чтобы быть параллельным очередному фронту волны, который будет сейчас принят, т.е. всё будет в соответствие с левым рис. 26. И в таком изменении углов наклона мембран в этой математической модели нет ничего искусственного, т.к. в действительности всё так и происходит на самом деле. Ведь никто не будет спорить, что маленький участок сферического фронта волны, созданной источником, всегда можно рассмотреть как плоскость, и эта плоскость всегда будет перпендикулярна лучу зрения с источника на приёмник в момент прихода к нему, а тарелки радиотелескопов во время наблюдений также всегда поворачивают так, чтобы их условная плоскость тоже была перпендикулярна лучу зрения.
Но на рис. 27, где я привожу скриншот формы 8 программы Dopler5m, у меня автоматически изменяется только угол наклона мембраны источника для каждого нового фронта волны так, чтобы при его приеме центр фронта совпадал с центром мембраны приемника, а вот угол наклона последней я в этом вычислительном эксперименте не изменяю. Таким образом, Вы видите, что 1-ый, 2-ой и 3-ий фронты плоских волн летят каждая в своем направлении, а угол наклона мембраны источника пока соответствует углу наклона 3-го фронта волны, т.к. еще не пришло время создавать 4-ый фронт волны.
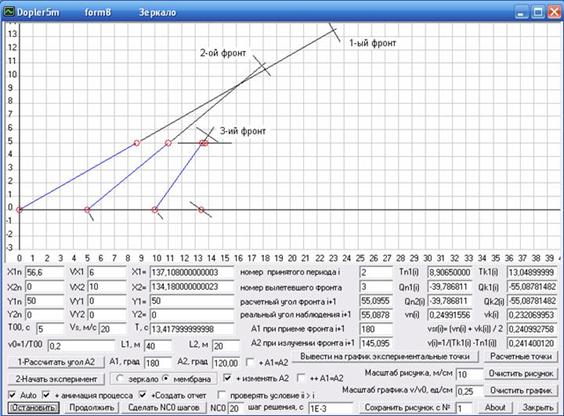
Рис. 27. Движение фронтов плоских волн от источника, мембрана которого всегда ориентирована на будущее положение приёмника, мембрана которого расположена горизонтально. Скриншот программы Dopler5m.
Теперь проверим код программы на форме 8 на наличие возможных ошибок в коде при регистрации среднего времени прихода фронта волны на приемник, когда мы его будем вычислять по двум значениям времени прихода левого и правого концов фронта волны. Для этого задаем те же самые параметры, что были на форме 1, но немного другие координаты источника и приемника, т.к. на форме 1 у нас по текущим координатам сначала рассчитывались запаздывающие координаты источника и приемника, а потом начиналось моделирование и за время одного периода координаты источника и приемника становились такими, как мы их задали, а на форме 8 моделирование сразу начинается с заданных текущих координат. Поэтому, с учетом того, что мы задаем период колебаний 5 с, то у нас, при заданных начальных координатах X1=56,6 м, X2=0 м, Y1=50 м и Y2=0 м, через 5 с координаты как раз и будут те, что были заданы на форме 1, т.е. X1=86,6 м, X2=50 м, Y1=50 м и Y2=0 м, а дальше расчет пойдет точно так же. Теперь нажимаем кнопку <Начать эксперимент> для варианта <мембрана>, а мембрану приемника располагаем горизонтально, чтобы она могла принимать сигналы от источника подлетающими к нему как с левой стороны, так и с правой, и после нескольких периодов смотрим отчет, данные которого заносим в таблицу 7. Как видим, они совпадают с теми, что приводились в табл. 6. Таким образом, хотя мы на форме 1 и рассматривали приемник как точку, а распространение сигнала рассматривали как распространение сферических фронтов, но эти расчеты относятся именно к ЭД, когда у нас источник и приемник мембранного типа и при этом экспериментальные данные хорошо аппроксимируются формулой (2).
Табл. 7. Наблюдаемые и расчётные данные частоты принимаемого сигнала при распространении сигнала с частотой передатчика 0,2 Гц для семи периодов сигнала (форма 8).
| № периода
| 1
| 2
| 3
| 4
| 5
| 6
| 7
|
| наблюдения
| 0,256
| 0,241
| 0,221
| 0,202
| 0,189
| 0,182
| 0,179
|
| формула (2)
| 0,256
| 0,241
| 0,221
| 0,202
| 0,189
| 0,183
| 0,179
|
Теперь давайте усложним нашу математическую модель на форме 1, чтобы мы могли моделировать и релятивистский ЭД, и рассматривать движение света не только в математической пустоте, но и в реальной среде с переменной оптической плотностью, а так же выполнить эксперименты в двух вариантах трактовки принципа относительности (ПО) Эйнштейна, т.е. когда и система тел (СТ), т.е. в нашем случае источник и приемник, движется в ИСО и наблюдения ведутся из этой ИСО, т.е. наблюдатель находится в этой же ИСО, и когда у нас СТ движется в одной ИСО (у меня это АСО), а наблюдаются эти тела из другой ИСО. А, т.к. при этом появится много дополнительных функций, и я не смогу их все разместить на формах 1 или 8 проекта, где мы моделировали классический ЭД в математической пустоте, то я создам две новые формы программы 3 (см. рис. 28) и 9 (см. рис.30). При этом на форме 3, где возможно движение в среде переменной оптической плотности, у меня классический ЭД с не увлекаемым эфиром моделируется только в АСО, а наблюдается из ИСО, а классический ЭД с увлекаемым эфиром и релятивистский ЭД моделируются только в ИСО и наблюдаются из этой же ИСО.
А на форме 9, где возможно движение только в среде постоянной оптической плотности, у меня классический ЭД с не увлекаемым эфиром и релятивистский ЭД могут моделироваться как в ИСО и наблюдаться из этой же ИСО, так и моделироваться в АСО, а наблюдаться из ИСО, т.е. здесь может проверяться ПО Эйнштейна в двух разных трактовках. При этом, если моделирование идет в ИСО и наблюдается из этой же ИСО, то я начальные координаты, скорости и время (заданные всегда в АСО) преобразую с использованием или преобразований Галилея или преобразований Лоренца из АСО в ИСО, а потом уже с этими начальными данными произвожу моделирование ЭД в ИСО. А, если моделирование идет в АСО и наблюдается из ИСО, то я с начальными координатами, скоростями и временем, которое всегда равно нулю, заданными в АСО, произвожу моделирование ЭД в АСО и потом по ходу вычислительного эксперимента преобразую с использованием или преобразований Галилея или преобразований Лоренца получающиеся текущие координаты и время из АСО в ИСО и эти координаты считаю наблюдаемыми из ИСО. Сначала давайте рассмотрим форму 3. Здесь у нас будет дискретно задаваться для нескольких сотен слоев среды, расположенных горизонтально, различная оптическая плотность среды, как выбором характера изменения плотности, так и заданием значения, на которое эта плотность будет изменяться между соседними слоями. При этом, скорость сигнала (пусть это будет свет) в разных слоях будет разной (но напоминаю, что частота сигнала при этом будет оставаться неизменной).

Рис. 28. Движение лучей света (синие кривые) от источника, который движется вдоль оси абсцисс из точки, когда он был в начале системы координат, к приёмнику, который движется параллельно на некоторой высоте на форме 3. Оптическая плотность среды при увеличении высоты уменьшается, что отражено синей наклонной прямой (в начале системы координат). Скриншот программы Dopler5m.
А т.к. у нас свет и будет распространяться в разных слоях с разной скоростью и будет преломляться при переходе от одного слоя к другому, я уже не смогу определять границу распространения света (сигнала) величиной сферы с радиусом Rs, как это было на форме 1. Поэтому я разбиваю всю сферу на множество очень мелких сегментов, которые буду считать просто отдельными лучами света и теперь у нас каждый луч света из большого пучка лучей пойдет своим путем и с разной скоростью. И мне придется теперь после каждого шага решения P0 определять новые координаты каждого луча света X22(j) и Y22(j), где j номер луча в пучке, и затем проверять достиг ли этот луч света приемника. Причем, если луч света будет идти из слоя с меньшей оптической плотностью в слой с большей оптической плотностью, то он всегда будет преломляться. А, если луч света будет идти из слоя с большей оптической плотностью в слой с меньшей оптической плотностью, то при угле падения большем, чем предельный угол, луч света будет отражаться, как это и показано для некоторых лучей на рис. 28. А момент времени, когда этот пучок света достигнет приемника, я теперь буду определять из условия того, что из двух соседних лучей один луч должен быть выше приемника, а другой ниже и при этом координата одного луча по оси абсцисс будет больше чем координата приемника, а другого меньше, как это показано на рис. 29, где координата 30-го луча в пучке по оси абсцисс больше, чем 29-го, а ордината наоборот меньше. При этом у нас теперь не будет единого угла наблюдения Q3, а будет два угла наблюдения Q31 для приемника и Q32 для источника, которые мы определим как средние значения этих углов для двух лучей 29-го и 30-го, которые, как говорят артиллеристы, взяли приемник в "вилку".
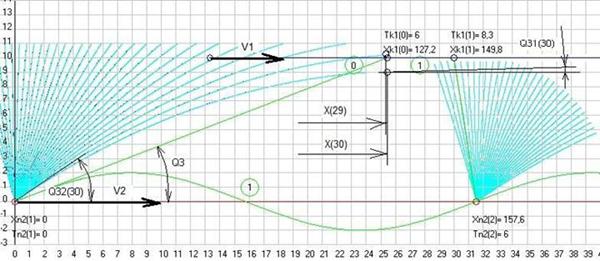
Рис. 29. Схема к расчету момента времени достижения сигналом приемника. Скриншот программы Dopler5.
Поэтому даже при одинаковых абсолютных углах скоростей V1 и V2, которые в нашем случае равны нулю, у нас будут разные относительные углы скоростей Q1 и Q2, которые нам теперь придется определять с использованием углов наблюдения Q31 и Q32. Ну, а все остальное будет так же, как это было у нас и при моделировании классического ЭД в математической пустоте, т.е. после заданного нами значения периода колебаний T00 мы начинаем формировать новый пучок лучей на источнике. При этом значение T00 должно быть не меньше максимального времени распространения сигнала от источника до приемника при любых их положениях, а иначе мы не сможем начать через время T00 формировать новый пучок лучей, т.к. предыдущий пучок еще не достигнет приемника, а в программе у меня предусмотрено моделирование только одного пучка лучей. И на рис. 29 мы видим, что при T00= 6 с начало 1-го периода колебаний было начато при Tn2(1)=0, а принят этот сигнал на приемнике, как время конца 0-го периода Tk1(0)= 6. После этого во время Tn2(2)= 6 начал передаваться сигнал начала 2-го периода, который достиг приемника во время Tk1(1)= 8,3 и затем во время Tn2(3)= 12 начнет передаваться сигнал о начале 3-го периода и т.д. Теперь, зная время Tk1(1)= 8,3 и Tk1(0)= 6, мы можем определить период принятого на приемнике сигнала 1-го периода 2,3 с и по нему среднюю частоту принятого сигнала между двумя положениями приемника, которая будет соответствовать среднему положению приемника между двумя координатами Xk1(0)=127,2 и Xk1(1)=149,8 и двумя положениями источника с координатами Xn2(1)=0 и Xn2(2)=157,6, которые дадут средний угол наблюдения.
При этом математическая модель релятивистского ЭД мало чем будет отличаться от математической модели классического ЭД, которую я приводил выше. Здесь точно так же источник и приемник будут двигаться с постоянными скоростями и, т.к. время в любой ИСО течет точно так же, как и в классике, равномерно во всех точках этой ИСО, то через один шаг решения координаты источника и приемника будут с учетом их скоростей в ИСО увеличиваться на маленькое приращение dX1=VX1iso*P0 для приемника и dX2=VX2iso*P0 для источника, а фронт сферической волны будет увеличивать свой радиус на величину dR=Vs*P0, где VX1iso и




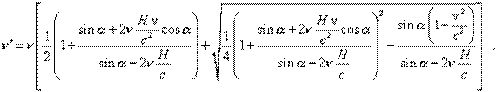 (10*)
(10*)













