Тема 3. Поля свободных элементарных частиц.

1. Скалярное вещественное поле.

2. Тензор энергии – импульса скалярного вещественного поля.

3. Импульсное представление функций скалярного вещественного поля.

4. Физическая интерпретация полевых и динамических величин.

 

Состояния свободных элементарных частиц являются идеальными. Реально свойства микрочастиц устанавливаются экспериментально в процессе взаимодействия. Однако, когда элементарные частицы находятся на очень больших расстояниях, когда взаимодействия между частицами пренебрежимо малы, можем рассматривать их как свободные.

Для определения квантовых свойств свободных полей элементарных частиц воспользуемся ковариантным лагранжевым формализмом и вариационными принципами.

В дальнейшем будем использовать естественную систему единиц измерения ħ=c=1, которая применяется в физике элементарных частиц.

 

Скалярное вещественное поле.

Как следует из релятивисткой квантовой механики, квантово – механические свойства бесспиновой частицы определяются из уравнения Клейна – Гордона – Фока:

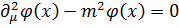                                            ,                                (3.1)

что согласуется с уравнением, которое следует из релятивисткой классической механики

                                                                                                 (3.2)

В самом деле, если воспользоваться соответствием

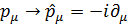
и учесть действие оператора 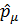 на волновую функцию , тогда из (3.2) следует (3.1).

В рамках ковариантного формализма Лагранжа уравнение (3.1) можно получить, воспользовавшись лагранжианом вида:

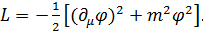                              (3.3)

В самом деле, согласно (1.24) справедливо уравнение Лагранжа- Эйлера

                                      (3.4)

Используя (3.3), получим

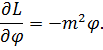
Подставляя эти выражения в (3.4), нетрудно видеть, что

 

Тензор энергии- импульса скалярного вещественного поля.

Используя лагранжиан (3.3) и определение тензора энергии-импульса (1.33), получим выражение для тензора энергии-импульса вещественного поля.

                                      (3.5)

Выражение 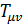 в данном случае принимает вид:

                    (3.6)

Энергия скалярного поля определяется

                  (3.7)

Из (3.7) очевидно, что 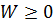. Используя (3.6), получим выражение для импульса поля

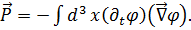                                 (3.8)

Поскольку поле вещественное, то четырёхмерная плотность тока равна нулю, т.е. функции этого поля описывают состояния нейтральных частиц, заряд которых равен нулю.

 

3.Импульсное представление функций скалярного вещественного поля

Общее решение дифференциального уравнения (3.1) имеет вид

                                          (3.9)

Если подставить экспоненты (3.9) в (3.1), то получим для одной экспоненты и для второй при фиксированном q следующее выражение

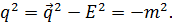                                                                            (3.10)

Таким образом, из (3.10) следует соотношение между энергией и импульсом для частицы, у которой масса покоя частицы отлична от нуля.

Поскольку полевая функция вещественна, то

                                                                                 (3.11)

В этом случае из (3.11) следует

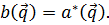
В результате (3.9) можно представить в виде

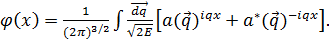                                            (3.12)

Вычислим теперь W и P, используя (3.12) и следующие общие соотношения:

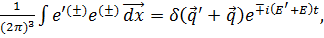                                                (3.13)

                                                (3.14)

 

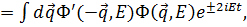                                                               (3.15)

 

     (3.16)

В этих выражениях введены обозначения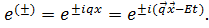

 Функции и 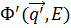 - множители, состоящие при экспонентах в (3.12).

Используя (3.12)-(3.16) и определение W (3.7) получим

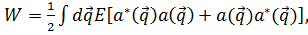                                                  (3.17)

                                               (3.18)

 

Физическая интерпретация

Полевые функции 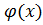 являются волновыми функциями релятивистского уравнения Клейна- Гордона- Фока (3.1):

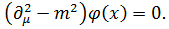
Решение этого уравнения представляется в виде суперпозиции «чистых состояний» с определенным значением 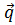 и

 

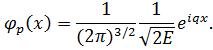
Частица массы 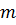 может находиться в одном из этих состояний. Согласно квантовой механики вероятность нахождения частицы в состоянии с импульсом  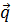и энергией   будет

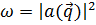
В этом случае выражения (2.17) и (2.18) можно интерпретировать, как среднее значение четырехмерного импульса поля

,

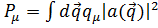где .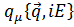

 

Тема 4. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В РЕЛЯТИВИСТСКИ-КОВАРИАНТНОЙ ФОРМЕ.

1. Электромагнитное поле.

2. Тензор энергии-импульса электромагнитного поля.

3. Импульсное представление электромагнитного поля.

 

Электромагнитное поле.

Как следует из электродинамики, лагранжиан электромагнитного поля имеет вид:

                                                                      (4.1)

Лагранжиан (4.1) определен через следующие четырехмерные величины:

- тензор электромагнитного поля

;

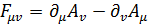- четырехмерный потенциал электромагнитного поля с компонентами

;

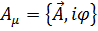- четырехмерную плотность тока с компонентами

.

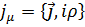Тензор электромагнитного поля можно представить в виде матрицы

,

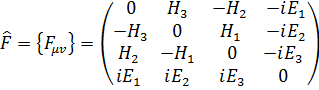где 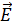- вектор напряженности электрического, а 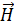- вектор напряженности магнитного полей.

Получим теперь уравнение Максвелла в четырехмерной форме.

Для этого воспользуемся уравнением (2.7) в котором 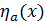 заменим на 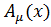. В этом случае

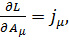                                                                                            (4.2)

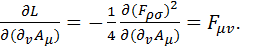                                                                   (4.3)

Таким образом из (4.2), (4.3) и (2.7) следует

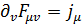                                              .                                                      (4.4)

В трехмерной форме уравнение (4.4) можно представить так:

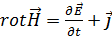                                               ,                                                (4.5)

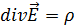                                                 .                                                     (4.6)

Остальные два уравнения Максвелла

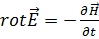                                                 ,                                                (4.7)

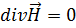                                                                                                       (4.8)

следуют из ковариантного уравнения вида

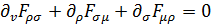                                   .                                      (4.9)

Переход к потенциальной форме описания электромагнитного поля осуществляется с помощью тензора электромагнитного поля. В трехмерной форме приходим к определению векторов напряженности электромагнитного поля через потенциалы:

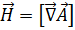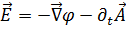                                    , .                                     (4.10)

В выражении (4.4) перейдем к уравнению через потенциалы, т.е. уравнению Даламбера:

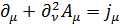.                                       (4.11)

Согласно инвариантности теории электромагнитного поля относительно калибровочных преобразований потенциал электромагнитного поля определяется неоднозначно

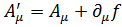.                                           (4.12)

Где 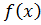 – произвольная функция.

Поскольку 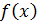произвольная функция, то можно выбрать такую функцию, чтобы

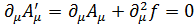                                   .                                    (4.13)

Тогда потенциалы 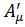 удовлетворяют условию Лоренца (4.13), когда функция  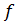является решением уравнения

                                                                             (4.14)

Если в (4.11) перейдем к новым потенциалам 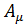, удовлетворяющим условию Лоренца

                                                                               (4.15)

то в результате получим уравнение Даламбера

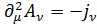                              ,                                                   (4.16)

Из выражения (4.16) следует, что для потенциалов свободного электромагнитного поля, когда нет взаимодействия, справедливо уравнение

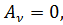□                                                 (4.17)

где □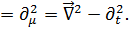  

Поскольку свободное электромагнитное поле определяется четырехмерными потенциалами 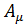, а в свою очередь, последние удовлетворяют двум уравнениям (4.15) и (4.17), то для описания свободного электромагнитного поля можно использовать две независимые компоненты.

Из уравнений (4.12) следует, что

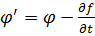                          .                                              (4.18)    

Так как 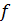  произвольная функция, удовлетворяющая только уравнению (4.14), то на выбор потенциала  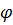можно наложить условие калибровки. Выберем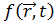 следующим образом                           

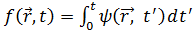                   .                                       (4.19)

Тогда уравнение (4.18) принимает вид

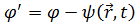                             .                                        (4.20)

В уравнении (4.20) функция 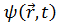 произвольная. Следовательно, можно использовать такую функцию 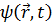, чтобы выполнялось соотношение

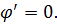                                                                                    (4.21)

Условие (4.21) называют условием кулоновской калибровки потенциалов.

Благодаря условиям (4.13) и (4.21) независимыми компонентами четырехмерного потенциала будут только две, что приводит к поперечной поляризации, относительно направления распространения свободного электромагнитного поля и векторный потенциал удовлетворяет соотношению

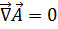                                       .                                                  (4.22)