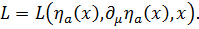Пусть, в общем случае, лагранжиан 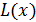 зависит от переменных
зависит от переменных 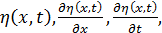 т.е.
т.е. 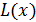 является функцией
является функцией
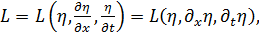 (1.8)
(1.8)
где 
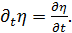
Функция действия определяется через 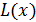 следующим образом:
следующим образом:
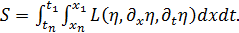 (1.9)
(1.9)
При варьировании функции S (1.9) будем использовать граничные условия
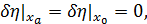 (1.10)
(1.10)
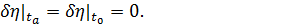 (1.11)
(1.11)
В этом случае вариацию функции действия можно привести к следующему виду
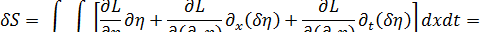
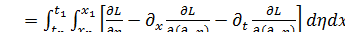 (1.12)
(1.12)
Таким образом, приравняв нулю 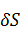 (1.12) согласно принципу наименьшего действия, получим уравнение Лагранжа-Эйлера для непрерывной системы.
(1.12) согласно принципу наименьшего действия, получим уравнение Лагранжа-Эйлера для непрерывной системы.
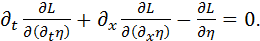 (1.13)
(1.13)
Например, используя лагранжиан (1.7) в уравнении (1.13) нетрудно убедиться, что
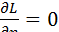 ,
, 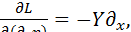
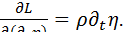
В результате получим уравнение
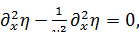 (1.14)
(1.14)
где 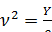 (1.15)
(1.15)
- скорость распространения продольных колебаний.
Уравнение (1.14) описывает распространение продольных возмущений вдоль одномерной струны со скоростью v.
В случае, когда лагранжиан 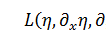 зависит от
зависит от  как функции 3-х переменных x,y,z и времени t
как функции 3-х переменных x,y,z и времени t
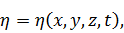
повторяя выше приведенное варьирование функции действия, а также, используя граничные условия и принцип наименьшего действия, получим
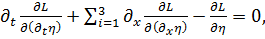 (1.16)
(1.16)
где 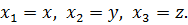
Если обобщенная координата непрерывной системы задается в виде компонент 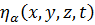 , то уравнение Лагранжа-Эйлера (1.16) записывается для каждой компоненты
, то уравнение Лагранжа-Эйлера (1.16) записывается для каждой компоненты 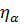 :
:
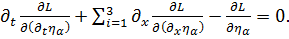 (1.17)
(1.17)
Тема 2. ЛАГРАНЖЕВ РЕЛЯТИВИСТСКИ-КОВАРИАНТНЫЙ ФОРМАЛИЗМ ДЛЯ НЕПРЕРЫВНЫХ СИСТЕМ.
1. Пространство Минковского и релятивистское обобщение метода Лагранжа.
2. Требования, предъявляемые к лагранжиану поля.
3. Тензор энергии-импульса непрерывной системы.
4. Плотность тока вероятности непрерывной системы.
Пространство Минковского и релятивистское обобщение метода Лагранжа.
Как следует из общих принципов специальной теории относительности и преобразований Лоренца при построении ковариантного описания непрерывной системы удобно объединить пространственные координаты и время в одно четырехмерное многообразие. Четырехмерный вектор определяется компонентами 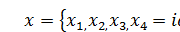
В этом случае квадрат 4-х- вектора 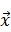 будет определяться следующим образом
будет определяться следующим образом
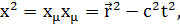 (2.1)
(2.1)
где µ пробегает значения 1, 2, 3, 4.
Согласно принципам теории относительности квадрат длинны четырех- мерного вектора (2.1) является инвариантом относительно преобразований Лоренца
 (2.2)
(2.2)
Из требования инвариантности (2.2) следует условие ортогональности преобразований Лоренца, т.е. если
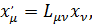 (2.3)
(2.3)
то матричные элемент 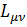 удовлетворяют условию
удовлетворяют условию
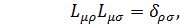 (2.4)
(2.4)
где 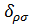 - символ Кронекера.
- символ Кронекера.
Частные преобразования Лоренца, когда выполняется переход в инерциальную систему отсчета, двигающуюся вдоль оси ОХ, имеют вид:
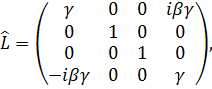 (2.5)
(2.5)
где 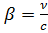 ,
, 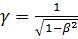
ν-скорость движения инерциальной системы отсчёта.
Нетрудно убедиться, что матрица вида (2.5) удовлетворяет условию ортогональности (2.4)
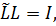 (2.6)
(2.6)
где 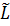 - транспонированная матрица.
- транспонированная матрица.
Требования, предъявляемые к лагранжиану поля.
В релятивистской теории поля уравнения движения должны иметь ковариантную форму относительно координат 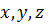 и времени
и времени  . Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени
. Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени 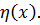 Лагранжиан непрерывной системы, который зависит от полевой функции
Лагранжиан непрерывной системы, который зависит от полевой функции 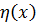 и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
Во-первых, Лагранжиан должен быть релятивистки инвариантной величиной, следовательно, полевые функции должны реализовать представление преобразований Лоренца.
Во-вторых, Лагранжиан должен быть вещественной величиной, поскольку, как известно из формализма Лагранжа, физически измеряемые величины выражаются через Лагранжиан.
В зависимости от типа релятивистских уравнений непрерывных систем вводятся дополнительные ограничения, например, такие как требование линейности, локальности, требование, чтобы Лагранжиан зависел от производных не выше второго порядка и т.д.
Учитывая эти требования, уравнения Лагранжа-Эйлера в релятивистской формулировке можно получить, используя принцип наименьшего действия в четырёхмерном пространстве – времени. Уравнения, которые следуют из вариационного принципа в релятивистской формулировке, совпадают с уравнениями (1.17), если в (1.17) перейти к четырехмерной форме.
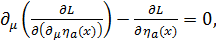 (2.7)
(2.7)
где 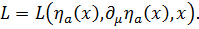



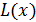 зависит от переменных
зависит от переменных 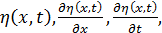 т.е.
т.е. 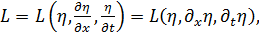 (1.8)
(1.8)
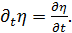
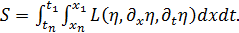 (1.9)
(1.9)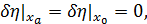 (1.10)
(1.10)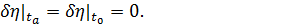 (1.11)
(1.11) 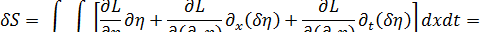
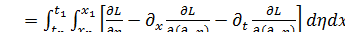 (1.12)
(1.12)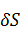 (1.12) согласно принципу наименьшего действия, получим уравнение Лагранжа-Эйлера для непрерывной системы.
(1.12) согласно принципу наименьшего действия, получим уравнение Лагранжа-Эйлера для непрерывной системы.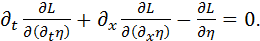 (1.13)
(1.13)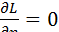 ,
, 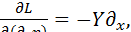
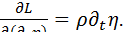
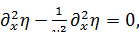 (1.14)
(1.14)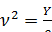 (1.15)
(1.15)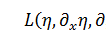 зависит от
зависит от  как функции 3-х переменных x,y,z и времени t
как функции 3-х переменных x,y,z и времени t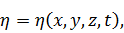
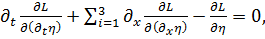 (1.16)
(1.16)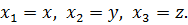
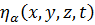 , то уравнение Лагранжа-Эйлера (1.16) записывается для каждой компоненты
, то уравнение Лагранжа-Эйлера (1.16) записывается для каждой компоненты 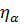 :
: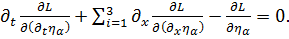 (1.17)
(1.17)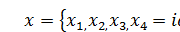
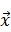 будет определяться следующим образом
будет определяться следующим образом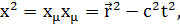 (2.1)
(2.1) (2.2)
(2.2)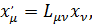 (2.3)
(2.3)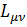 удовлетворяют условию
удовлетворяют условию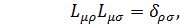 (2.4)
(2.4)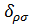 - символ Кронекера.
- символ Кронекера.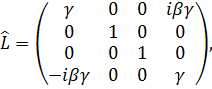 (2.5)
(2.5)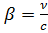 ,
, 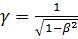
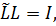 (2.6)
(2.6) 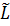 - транспонированная матрица.
- транспонированная матрица.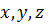 и времени
и времени  . Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени
. Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени 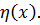 Лагранжиан непрерывной системы, который зависит от полевой функции
Лагранжиан непрерывной системы, который зависит от полевой функции 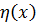 и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.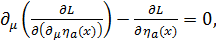 (2.7)
(2.7)