БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени академика И.Г. Петровского
филиал в г. Новозыбкове
кафедра математики, физики и информатики
Н.В.Максименко, Е.В.Вакулина,
О.М. Дерюжкова, С.М. Кучин.
Теоретико-полевые основы электродинамических процессов
БРЯНСК 2010
Федеральное агентство по образованию РФ
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени академика И.Г. Петровского
филиал в г. Новозыбкове
кафедра математики, физики и информатики
Н.В.Максименко, Е.В.Вакулина,
О.М. Дерюжкова, С.М. Кучин.
Теоретико-полевые основы электродинамических процессов
УЧЕБНОЕ ПОСОБИЕ
Рекомендовано учебно-методическим советом филиала БГУ в г.Новозыбкове в качестве учебного пособия для студентов физико-математических специальностей педагогических вузов
БРЯНСК 2010
ББК 22.161.68я73
Рецензенты
Андреев В.В.- заведующий кафедрой теоретической физики УО “ГГУ им. Ф. Скорины”, доцент, кандидат физико-математических наук.
Бабич А.А.- заведующий кафедрой высшей математики УО “ГГТУ им. П.О. Сухого”, доцент, кандидат физико-математических наук.
Максименко Н.В, Вакулина Е.В, Дерюжкова О.М, Кучин С.М. “ Теоретико-полевые основы электродинамических процессов ”. Учебное пособие спецкурса для студентов физико-математических специальностей.-Брянск: РИО БГУ, 2010.-56с.
ISBN//////////////////////////
Учебное пособие содержит необходимые современные теоретические элементы методов расчета электродинамических процессов элементарных частиц. Изложена теория взаимодействующих полей на ковариантного метода функций Грина в рамках теории возмущений и асимптотических приближений. В доступной форме показано получение основных соотношений, необходимых для проведения расчетов вероятностей распадов и сечений процессов.
ББК 22.161.68я73
ISBN////////////////////////// Максименко Н.В. и др, текст, 2010
РИО БГУ, 2010
ОГЛАВЛЕНИЕ
Предисловие… …………………………………………………………………..
Тема 1. Лагранжев формализм для непрерывных систем. ……………….
1. Переход от дискретной системы к непрерывной…………………………….
2. Вариационный принцип для непрерывной одномерной системы (принцип наименьшего действия)…………………………………………………………..
Тема 2. Лагранжев релятивистски-ковариантный формализм для непрерывных систем ……………………………………………………………
1.Пространство Минковского и релятивистское обобщение метода Лагранжа…………………………………………………………………………….
2.Требования, предъявляемые к лагранжиану поля………………………....
3.Тензор энергии-импульса непрерывной системы…………………………….
4. Плотность тока вероятности непрерывной системы………………………...
Тема 3. Поля свободных элементарных частиц… …………………………..
1.Скалярное вещественное поле………………………………………………..
2.Тензор энергии – импульса скалярного вещественного поля……………..
3.Импульсное представление функций скалярного вещественного поля…..
4.Физическая интерпретация полевых и динамических величин……………..
Тема 4. Уравнения электромагнитного поля в релятивистски-ковариантной форме… …………………………………………………………
1.Электромагнитное поле………………………………………………………..
2.Тензор энергии-импульса электромагнитного поля…………………………
3.Импульсное представление электромагнитного поля……………………….
Тема 5. Релятивистски-ковариантная форма уравнений Дирака… …….
1.Уравнение Дирака………………………………………………………………
2.Определение оператора спина дираковских частиц………………………….
3.Лагранжев формализм поля Дирака…………………………………………..
4.Решение уравнения Дирака и определение динамических переменных в импульсном представлении……………………………………………………..
Тема 6. Взаимодействие заряженных частиц с электромагнитным полем… …………………………………………………………………………..
1.Лагранжев формализм взаимодействия электромагнитного поля с заряженными частицами…………………………………………………………
2.Принцип локальной калибровочной инвариантности в теории взаимодействующих полей………………………………………………………
3.Закон сохранения тока, как следствие принципа калибровочной инвариантности…………………………………………………………………..
Тема 7. Решение уравнений для взаимодействующих полей методом теории возмущений на основе функции Грина… ………………………….
1.Решение полевых уравнений движения на основе функции Грина………..
2.Функция Грина спинорного и фотонного полей…………………………….
3.Определение амплитуды процессов взаимодействия фотонов с заряженными частицами в рамках теории возмущений………………………
Тема 8. Рассеяние электронов в кулоновском поле… ……………………
1.Определение амплитуды рассеяния электронов в кулоновском поле……
2.Определение сечений рассеяния электронов в кулоновском поле……….
3.Вычисление следов 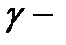 частиц и кинематических соотношений процесса рассеяния…………………………………………………………………………
частиц и кинематических соотношений процесса рассеяния…………………………………………………………………………
Библиографический список ……………………………………………………
ПРЕДИСЛОВИЕ
Настоящее пособие представляет собой попытку в простом варианте изложить квантовомеханические основы расчетов электродинамических процессов в рамках классической теории полей, сопоставляемых элементарным частицам. При написании пособия использован материал спецкурсов, прочитанных в Гомельском университете им. Ф. Скорины и Новозыбковском филиале Брянского государственного университета им. И.Г. Петровского.
Содержание и методическая компоновка пособия определилась прежде всего тем, чтобы оно было доступным и могло служить основой для последующего, более углубленного, изучения квантовой теории поля и физики элементарных частиц.
Теория поля может быть построена по аналогии и использовании математического аппарата классической механики систем материальных точек. В рамках классической механики мы встречаемся с системами, которые следует рассматривать как непрерывные. Поэтому в пособии в начале рассматривается пример перехода от дискретной механической системы к непрерывной в рамках формализма Лагранжа, который наиболее приспособлен для последующего описания релятивистских непрерывных систем.
Учитывая в лагранжевом формализме постулаты специальной теории относительности и дополняя вариационные принципы аналитической механики требованиями релятивистской теории, определены динамические переменные в четырехмерном пространстве-времени, тем самым установлены релятивистские уравнения движения для электромагнитного поля, а также скалярных и спинорных частиц.
Уравнения взаимодействия электромагнитного поля с заряженными частицами получены на основе принципов калибровочной инвариантности. Для решения этих уравнений определены в рамках ковариантного метода функций Грина (метода функций распределения). Затем, используя методы теории возмущений и свойства полевых функций на асимптотике, определены амплитуды и сечения конкретных электродинамических процессов.
В основе современной теории элементарных частиц лежат понятия полей. Каждому типу элементарных частиц сопоставляется своё поле. Посредством квантов поля осуществляется взаимодействие. Считается, что задана полевая функция, если каждой точке пространства и времени ставится в соответствие одна или несколько величин 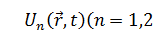 . Полевые функции удовлетворяют определенным дифференциальным уравнениям движения, которые содержат информацию о физическом состоянии физической системы.
. Полевые функции удовлетворяют определенным дифференциальным уравнениям движения, которые содержат информацию о физическом состоянии физической системы.
Классические поля, соответствующие определённым элементарным частицам, являются непрерывными волновыми функциями, обладающими определенными трансформационными свойствами относительно преобразования пространственно-временных координат.
Одним из наиболее подходящих формализмов для построения уравнений движения для полевых функций является математический аппарат непрерывных систем, в котором используются вариационные принципы. В системе вариационных принципов лагранжев формализм более приспособлен для учета квантовомеханических и трансформационных релятивистских свойств элементарных частиц.
Тема 2. ЛАГРАНЖЕВ РЕЛЯТИВИСТСКИ-КОВАРИАНТНЫЙ ФОРМАЛИЗМ ДЛЯ НЕПРЕРЫВНЫХ СИСТЕМ.
1. Пространство Минковского и релятивистское обобщение метода Лагранжа.
2. Требования, предъявляемые к лагранжиану поля.
3. Тензор энергии-импульса непрерывной системы.
4. Плотность тока вероятности непрерывной системы.
Требования, предъявляемые к лагранжиану поля.
В релятивистской теории поля уравнения движения должны иметь ковариантную форму относительно координат 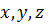 и времени
и времени  . Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени
. Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени 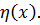 Лагранжиан непрерывной системы, который зависит от полевой функции
Лагранжиан непрерывной системы, который зависит от полевой функции 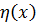 и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
Во-первых, Лагранжиан должен быть релятивистки инвариантной величиной, следовательно, полевые функции должны реализовать представление преобразований Лоренца.
Во-вторых, Лагранжиан должен быть вещественной величиной, поскольку, как известно из формализма Лагранжа, физически измеряемые величины выражаются через Лагранжиан.
В зависимости от типа релятивистских уравнений непрерывных систем вводятся дополнительные ограничения, например, такие как требование линейности, локальности, требование, чтобы Лагранжиан зависел от производных не выше второго порядка и т.д.
Учитывая эти требования, уравнения Лагранжа-Эйлера в релятивистской формулировке можно получить, используя принцип наименьшего действия в четырёхмерном пространстве – времени. Уравнения, которые следуют из вариационного принципа в релятивистской формулировке, совпадают с уравнениями (1.17), если в (1.17) перейти к четырехмерной форме.
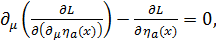 (2.7)
(2.7)
где 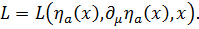
Физическая интерпретация
Полевые функции 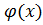 являются волновыми функциями релятивистского уравнения Клейна- Гордона- Фока (3.1):
являются волновыми функциями релятивистского уравнения Клейна- Гордона- Фока (3.1):
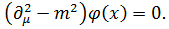
Решение этого уравнения представляется в виде суперпозиции «чистых состояний» с определенным значением 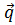 и
и 
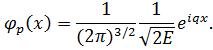
Частица массы 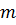 может находиться в одном из этих состояний. Согласно квантовой механики вероятность нахождения частицы в состоянии с импульсом
может находиться в одном из этих состояний. Согласно квантовой механики вероятность нахождения частицы в состоянии с импульсом 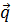 и энергией
и энергией  будет
будет
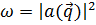
В этом случае выражения (2.17) и (2.18) можно интерпретировать, как среднее значение четырехмерного импульса поля
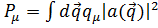 ,
,
где 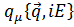 .
.
Тема 4. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В РЕЛЯТИВИСТСКИ-КОВАРИАНТНОЙ ФОРМЕ.
1. Электромагнитное поле.
2. Тензор энергии-импульса электромагнитного поля.
3. Импульсное представление электромагнитного поля.
Электромагнитное поле.
Как следует из электродинамики, лагранжиан электромагнитного поля имеет вид:
 (4.1)
(4.1)
Лагранжиан (4.1) определен через следующие четырехмерные величины:
- тензор электромагнитного поля
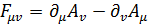 ;
;
- четырехмерный потенциал электромагнитного поля с компонентами
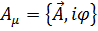 ;
;
- четырехмерную плотность тока с компонентами
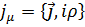 .
.
Тензор электромагнитного поля можно представить в виде матрицы
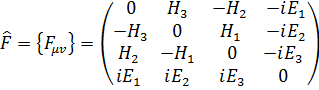 ,
,
где 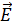 - вектор напряженности электрического, а
- вектор напряженности электрического, а 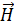 - вектор напряженности магнитного полей.
- вектор напряженности магнитного полей.
Получим теперь уравнение Максвелла в четырехмерной форме.
Для этого воспользуемся уравнением (2.7) в котором 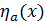 заменим на
заменим на 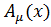 . В этом случае
. В этом случае
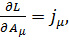 (4.2)
(4.2)
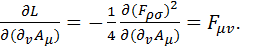 (4.3)
(4.3)
Таким образом из (4.2), (4.3) и (2.7) следует
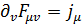 . (4.4)
. (4.4)
В трехмерной форме уравнение (4.4) можно представить так:
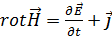 , (4.5)
, (4.5)
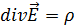 . (4.6)
. (4.6)
Остальные два уравнения Максвелла
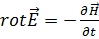 , (4.7)
, (4.7)
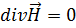 (4.8)
(4.8)
следуют из ковариантного уравнения вида
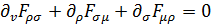 . (4.9)
. (4.9)
Переход к потенциальной форме описания электромагнитного поля осуществляется с помощью тензора электромагнитного поля. В трехмерной форме приходим к определению векторов напряженности электромагнитного поля через потенциалы:
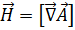 ,
, 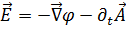 . (4.10)
. (4.10)
В выражении (4.4) перейдем к уравнению через потенциалы, т.е. уравнению Даламбера:
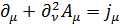 . (4.11)
. (4.11)
Согласно инвариантности теории электромагнитного поля относительно калибровочных преобразований потенциал электромагнитного поля определяется неоднозначно
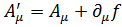 . (4.12)
. (4.12)
Где 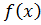 – произвольная функция.
– произвольная функция.
Поскольку 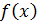 произвольная функция, то можно выбрать такую функцию, чтобы
произвольная функция, то можно выбрать такую функцию, чтобы
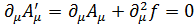 . (4.13)
. (4.13)
Тогда потенциалы 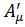 удовлетворяют условию Лоренца (4.13), когда функция
удовлетворяют условию Лоренца (4.13), когда функция 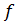 является решением уравнения
является решением уравнения
 (4.14)
(4.14)
Если в (4.11) перейдем к новым потенциалам 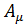 , удовлетворяющим условию Лоренца
, удовлетворяющим условию Лоренца
 (4.15)
(4.15)
то в результате получим уравнение Даламбера

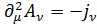 , (4.16)
, (4.16)
Из выражения (4.16) следует, что для потенциалов свободного электромагнитного поля, когда нет взаимодействия, справедливо уравнение
□ 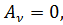 (4.17)
(4.17)
где □ 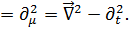
Поскольку свободное электромагнитное поле определяется четырехмерными потенциалами 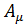 , а в свою очередь, последние удовлетворяют двум уравнениям (4.15) и (4.17), то для описания свободного электромагнитного поля можно использовать две независимые компоненты.
, а в свою очередь, последние удовлетворяют двум уравнениям (4.15) и (4.17), то для описания свободного электромагнитного поля можно использовать две независимые компоненты.
Из уравнений (4.12) следует, что
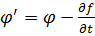 . (4.18)
. (4.18)
Так как 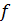 произвольная функция, удовлетворяющая только уравнению (4.14), то на выбор потенциала
произвольная функция, удовлетворяющая только уравнению (4.14), то на выбор потенциала 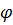 можно наложить условие калибровки. Выберем
можно наложить условие калибровки. Выберем 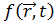
 следующим образом
следующим образом


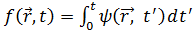 . (4.19)
. (4.19)
Тогда уравнение (4.18) принимает вид
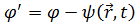 . (4.20)
. (4.20)
В уравнении (4.20) функция 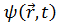 произвольная. Следовательно, можно использовать такую функцию
произвольная. Следовательно, можно использовать такую функцию 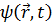 , чтобы выполнялось соотношение
, чтобы выполнялось соотношение
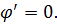 (4.21)
(4.21)
Условие (4.21) называют условием кулоновской калибровки потенциалов.
Благодаря условиям (4.13) и (4.21) независимыми компонентами четырехмерного потенциала будут только две, что приводит к поперечной поляризации, относительно направления распространения свободного электромагнитного поля и векторный потенциал удовлетворяет соотношению
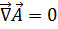 . (4.22)
. (4.22)
Тема 5. РЕЛЯТИВИСТСКИ-КОВАРИАНТНАЯ ФОРМА УРАВНЕНИЯ ДИРАКА.
1. Уравнение Дирака
2. Определение оператора спина дираковских частиц
3. Лагранжев формализм поля Дирака
4. Решение уравнения Дирака и определение динамических переменных в импульсном представлении
Уравнение Дирака
Согласно релятивисткой квантовой механике уравнение Дирака в ковариантной форме имеет вид:
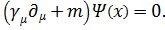 (5.1)
(5.1)
В уравнении (5.1) матрицы 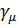 размерности
размерности 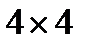 и удовлетворяют перестановочным соотношениям
и удовлетворяют перестановочным соотношениям
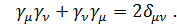 (5.2)
(5.2)
Перестановочные соотношения (5.2) обусловлены тем, что из уравнения Дирака (5.1) следует уравнение непрерывности для плотности тока вероятности и каждая компонента волновой функции 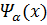 (
(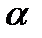 принимает значения 1,2,3,4) удовлетворяет релятивистскому уравнению КГФ
принимает значения 1,2,3,4) удовлетворяет релятивистскому уравнению КГФ
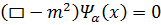 (5.3)
(5.3)
Из уравнения (5.1) и определения дираковски-сопряженной волновой функции
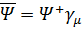 (5.4)
(5.4)
следует уравнение
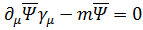 . (5.5)
. (5.5)
Матрицы 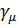 , удовлетворяющие (5.2), можно выразить через матрицы Паули
, удовлетворяющие (5.2), можно выразить через матрицы Паули 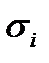 , которые удовлетворяют следующим перестановочным соотношениям:
, которые удовлетворяют следующим перестановочным соотношениям:
 (5.6)
(5.6)
Эти матрицы образуют полный набор матриц размерности 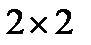 .
.
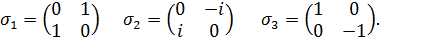 (5.7)
(5.7)
Нетрудно убедиться, что матрицы 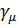 , которые имеют вид
, которые имеют вид
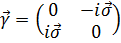
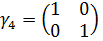 (5.8)
(5.8)
удовлетворяют перестановочным соотношениям (5.2).
Уравнение (5.1) приведем к форме типа уравнения Шредингера, что позволит определить оператор Гамильтона уравнения Дирака. Для этого с помощью матриц (5.8) введем матрицы матрицы 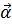 и
и 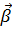 :
:
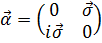 ,
, 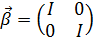 (5.9)
(5.9)
Которые связаны с 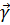 -матрицами через соотношение
-матрицами через соотношение 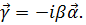 Таким образом, используя матрицы (5.9) и уравнения (5.1), получим
Таким образом, используя матрицы (5.9) и уравнения (5.1), получим
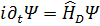 (5.10)
(5.10)
где 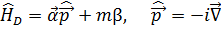 .
.
Библиографический список.
1. Бьёркен, Д.Д. Релятивистская квантовая теория поля: в 2 т. /Д.Д. Бьёркен, С.Д. Дрелл.- Москва:Наука,1978.- Т.1:Релятивистская квантовая механика. -296с.
2. Богуш, А. А. Введение в теорию классических полей / А. А. Богуш, Л.Г. Мороз. — Минск: Наука и техника, 1968. — 387 с.
3. Богуш, А.А. Введение в калибровочную полевую теорию электрослабых взаимодействий / А.А. Богуш. –Минск: Наука и техника, 1987.-359с.
4. Биленкий, С.М. Введение в диаграммную технику Фейнмана: учеб. пособие для вузов / С.М. Биленкий-1-е изд. –М.: Атомиздат, 1971. -215 с.С.М.
5. Москалёв, А.Н. Релятивистская теория поля / А.Н. Москалев.- Санкт-Петербург, 2006.-206с.
6. Гальцов, Д.В. Классические поля / Д.В. Гальцов, Ю.В. Грац, В.И. Жуковский. -изд. МГУ, 1991.-150с.
БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
имени академика И.Г. Петровского
филиал в г. Новозыбкове
кафедра математики, физики и информатики
Н.В.Максименко, Е.В.Вакулина,
О.М. Дерюжкова, С.М. Кучин.



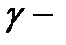 частиц и кинематических соотношений процесса рассеяния…………………………………………………………………………
частиц и кинематических соотношений процесса рассеяния…………………………………………………………………………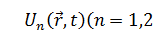 . Полевые функции удовлетворяют определенным дифференциальным уравнениям движения, которые содержат информацию о физическом состоянии физической системы.
. Полевые функции удовлетворяют определенным дифференциальным уравнениям движения, которые содержат информацию о физическом состоянии физической системы.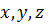 и времени
и времени  . Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени
. Лагранжев формализм является наиболее подходящим для релятивистского описания полей, соответствующих определенным элементарным частицам. Для этого будем считать, что функции непрерывных систем определяются в точке четырёхмерного пространства – времени 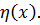 Лагранжиан непрерывной системы, который зависит от полевой функции
Лагранжиан непрерывной системы, который зависит от полевой функции 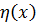 и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.
и четырёхмерных производных от этой функции, должен удовлетворять определённым требованиям. Эти требования следуют из основных принципов релятивистской теории и квантовой механики.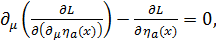 (2.7)
(2.7)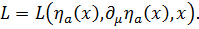
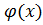 являются волновыми функциями релятивистского уравнения Клейна- Гордона- Фока (3.1):
являются волновыми функциями релятивистского уравнения Клейна- Гордона- Фока (3.1):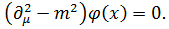
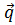 и
и 
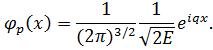
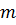 может находиться в одном из этих состояний. Согласно квантовой механики вероятность нахождения частицы в состоянии с импульсом
может находиться в одном из этих состояний. Согласно квантовой механики вероятность нахождения частицы в состоянии с импульсом 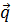 и энергией
и энергией 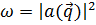
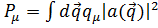 ,
,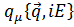 .
. (4.1)
(4.1)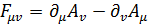 ;
;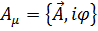 ;
;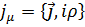 .
.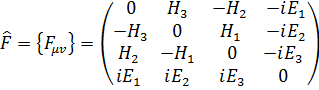 ,
,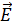 - вектор напряженности электрического, а
- вектор напряженности электрического, а 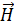 - вектор напряженности магнитного полей.
- вектор напряженности магнитного полей.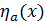 заменим на
заменим на 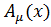 . В этом случае
. В этом случае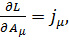 (4.2)
(4.2)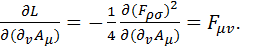 (4.3)
(4.3)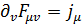 . (4.4)
. (4.4)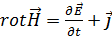 , (4.5)
, (4.5)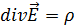 . (4.6)
. (4.6)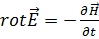 , (4.7)
, (4.7)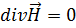 (4.8)
(4.8)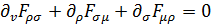 . (4.9)
. (4.9)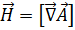 ,
, 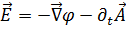 . (4.10)
. (4.10)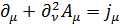 . (4.11)
. (4.11)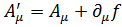 . (4.12)
. (4.12)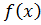 – произвольная функция.
– произвольная функция.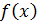 произвольная функция, то можно выбрать такую функцию, чтобы
произвольная функция, то можно выбрать такую функцию, чтобы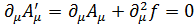 . (4.13)
. (4.13)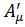 удовлетворяют условию Лоренца (4.13), когда функция
удовлетворяют условию Лоренца (4.13), когда функция 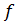 является решением уравнения
является решением уравнения (4.14)
(4.14)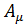 , удовлетворяющим условию Лоренца
, удовлетворяющим условию Лоренца (4.15)
(4.15)
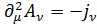 , (4.16)
, (4.16)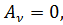 (4.17)
(4.17)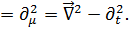
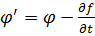 . (4.18)
. (4.18) 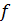 произвольная функция, удовлетворяющая только уравнению (4.14), то на выбор потенциала
произвольная функция, удовлетворяющая только уравнению (4.14), то на выбор потенциала 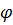 можно наложить условие калибровки. Выберем
можно наложить условие калибровки. Выберем 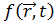

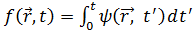 . (4.19)
. (4.19)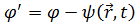 . (4.20)
. (4.20)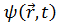 произвольная. Следовательно, можно использовать такую функцию
произвольная. Следовательно, можно использовать такую функцию 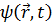 , чтобы выполнялось соотношение
, чтобы выполнялось соотношение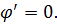 (4.21)
(4.21)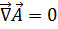 . (4.22)
. (4.22)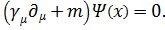 (5.1)
(5.1)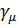 размерности
размерности 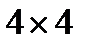 и удовлетворяют перестановочным соотношениям
и удовлетворяют перестановочным соотношениям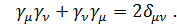 (5.2)
(5.2)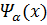 (
(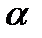 принимает значения 1,2,3,4) удовлетворяет релятивистскому уравнению КГФ
принимает значения 1,2,3,4) удовлетворяет релятивистскому уравнению КГФ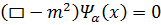 (5.3)
(5.3) 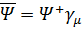 (5.4)
(5.4)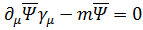 . (5.5)
. (5.5)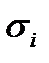 , которые удовлетворяют следующим перестановочным соотношениям:
, которые удовлетворяют следующим перестановочным соотношениям: (5.6)
(5.6)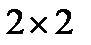 .
.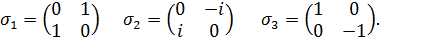 (5.7)
(5.7)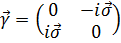
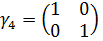 (5.8)
(5.8)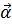 и
и 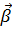 :
: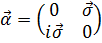 ,
, 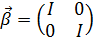 (5.9)
(5.9)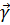 -матрицами через соотношение
-матрицами через соотношение 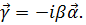 Таким образом, используя матрицы (5.9) и уравнения (5.1), получим
Таким образом, используя матрицы (5.9) и уравнения (5.1), получим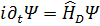 (5.10)
(5.10)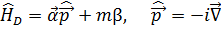 .
.

