Пример 1. 
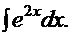
Рецепт. Вводим замену 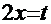 . Отсюда:
. Отсюда: 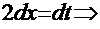 (вспомним формулу дифференциала)
(вспомним формулу дифференциала) 
 . Тогда
. Тогда 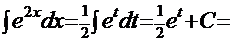 (обратная подстановка)
(обратная подстановка) 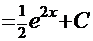 .
.
Пример 2. 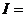
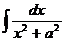
В таблице элементарных интегралов имеется формула аналогичного интеграла:
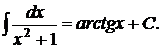 Однако чаще же всего встречается более общий вариант этого интеграла:
Однако чаще же всего встречается более общий вариант этого интеграла: 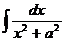 , где
, где 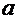 ─ некая числовая константа.
─ некая числовая константа.
Рецепт. Выносим  из знаменателя (а, значит, и из-под знака интеграла):
из знаменателя (а, значит, и из-под знака интеграла):
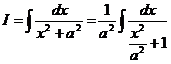 и делаем замену:
и делаем замену: 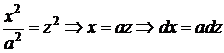 . Тогда
. Тогда 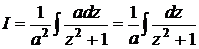 . А это уже знакомый табличный интеграл. Отсюда
. А это уже знакомый табличный интеграл. Отсюда 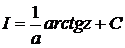 . Проводим обратную подстановку
. Проводим обратную подстановку 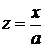 и получаем в результате
и получаем в результате 
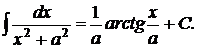
Полученным интегралом рекомендуем пополнить уже имеющуюся таблицу.
Приведение к «табличному виду».
Пример 3. 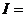
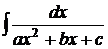 Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Рецепт. Преобразуем трёхчлен знаменателя к виду, похожему на квадратный двучлен табличного интеграла, рассмотренного в Примере 2. Последовательность действий должна быть следующей:
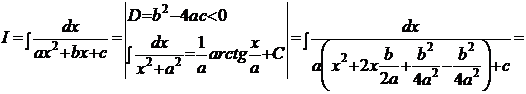
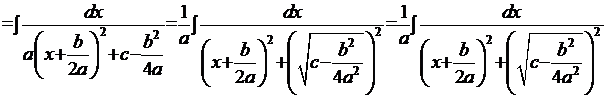
Очевидно, что этот интеграл по своей структуре полностью соответствует интегралу Примера 2: переменной 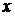 этого интеграла соответствует переменная
этого интеграла соответствует переменная  , а множителю
, а множителю  соответствует радикал:
соответствует радикал: 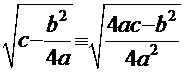
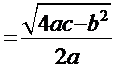 . Далее
. Далее 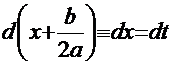 . Отсюда решение интеграла:
. Отсюда решение интеграла: 

N.B.! Помните, что нельзя полностью доверять авторам любого учебного пособия (кто из нас не без греха?), в том числе и авторам данного пособия. Поэтому убедительная просьба: для проверки правильности взятия интеграла старайтесь почаще применять первое свойство интегралов!
Замена функции.
Для этого приёма характерно многообразие вариантов замены какой-либо функции, входящей в подынтегральную функцию. Удача чаще всего приходит только в случае перебора нескольких вариантов.
Пример 4.  .
.
Рецепт. Здесь безальтернативный вариант замены:  . Это – табличный интеграл:
. Это – табличный интеграл: 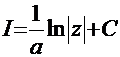 . Обратная подстановка
. Обратная подстановка  приводит к конечному результату:
приводит к конечному результату:  .
.
Пример 5. 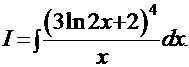
Рецепт. Опытный взгляд обнаружит интересную дробь  ─ дифференциал функции
─ дифференциал функции 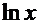 , а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену:
, а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену: 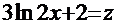 . Тогда
. Тогда 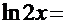


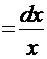
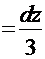 . В результате этой подстановки имеем табличный интеграл:
. В результате этой подстановки имеем табличный интеграл: 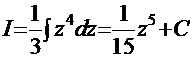 . Обратная подстановка приводит к конечному результату
. Обратная подстановка приводит к конечному результату 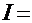
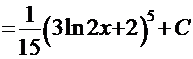 .
.
К этой же группе интегралов, требующих замены функции, относятся такие, в составе которых имеются радикалы 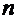 ой степени
ой степени 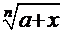 , т.е. компоненты типа
, т.е. компоненты типа 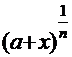 . Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
. Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
Пример 6. 
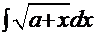 .
.
Рецепт. Здесь 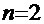 . Очевидна замена
. Очевидна замена 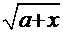 =
= 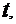 тогда
тогда 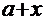 =
= 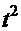


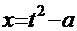

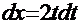 . Тогда интеграл легко приводится к
. Тогда интеграл легко приводится к 
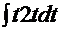 = =
= = 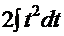
 +С.
+С.
Обратная подстановка даёт конечный результат: 
 =
= 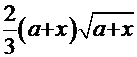 +С.
+С.
Интегрирование «по частям»
Идея этого метода основана на формуле производной произведения двух функций: 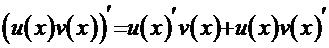 [1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций:
[1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций: 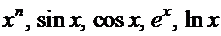 и их вариаций.
и их вариаций.
Итак, если подынтегральную функцию 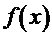 можно представить в виде произведения
можно представить в виде произведения 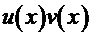 , то сочетание
, то сочетание 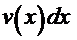 или
или  можно принять за дифференциал
можно принять за дифференциал 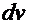 или
или 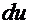 . Тогда решение интеграла получается по формуле:
. Тогда решение интеграла получается по формуле: 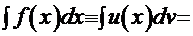

Выбор функций-сомножителей определяется опытом самого решающего. Попытаемся показать это на конкретном примере.
Пример 7.  .
.
Рецепт. Альтернатива выбора функций-сомножителей здесь небогатая: либо 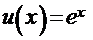 и
и 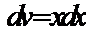 , либо
, либо 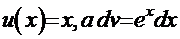 . Попробуем пойти первым путём
. Попробуем пойти первым путём
Вариант 1. 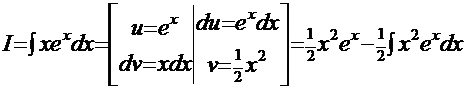 . Повторно применяем этот же метод:
. Повторно применяем этот же метод:  и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции
и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции 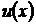 .
.
Не следует думать, что есть люди, которые ни разу не совершали подобную ошибку, просто из этого надо сделать позитивный вывод: «на ошибках учатся».
А теперь пойдём альтернативным путём:
Вариант 2: 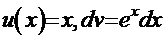 . Тогда
. Тогда 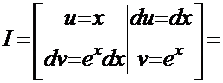
 .
.
Интересной особенностью данного метода является решение «рекурсивных интегралов». Рассмотрим один из вариантов таких интегралов.
Пример 8. 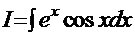 .
.
Рецепт. Применим метод «по частям»: 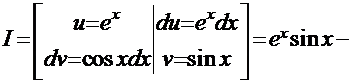
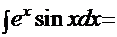


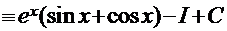
Сопоставив начало и конец этой цепочки, получаем решение 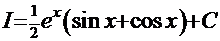 .
.
5. Рациональные дроби
Известно [1], что дробь может называться «рациональной», если её числитель и знаменатель ─ целые числа. С этой точки зрения излагаемый дальше метод относится к интегралам вида: 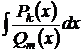 , где
, где  , а
, а 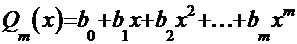 ─ полиномы порядка
─ полиномы порядка 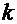 и
и  , соответственно.
, соответственно.
С точки зрения соотношения порядков полиномов возможны два варианта:
a)  . В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов:
. В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов: 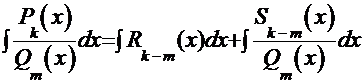 , где
, где 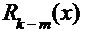
и 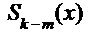 ─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
b) 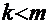 . Здесь сразу берётся интеграл указанным выше методом.
. Здесь сразу берётся интеграл указанным выше методом.




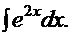
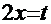 . Отсюда:
. Отсюда: 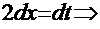 (вспомним формулу дифференциала)
(вспомним формулу дифференциала) 
 . Тогда
. Тогда 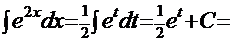 (обратная подстановка)
(обратная подстановка) 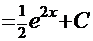 .
.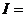
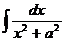
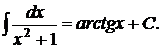 Однако чаще же всего встречается более общий вариант этого интеграла:
Однако чаще же всего встречается более общий вариант этого интеграла: 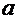 ─ некая числовая константа.
─ некая числовая константа. из знаменателя (а, значит, и из-под знака интеграла):
из знаменателя (а, значит, и из-под знака интеграла):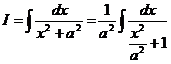 и делаем замену:
и делаем замену: 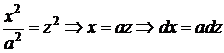 . Тогда
. Тогда 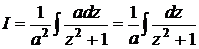 . А это уже знакомый табличный интеграл. Отсюда
. А это уже знакомый табличный интеграл. Отсюда 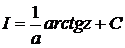 . Проводим обратную подстановку
. Проводим обратную подстановку 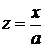 и получаем в результате
и получаем в результате 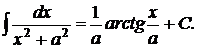
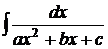 Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).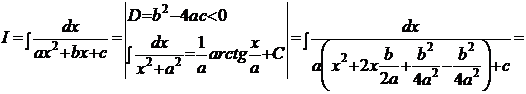
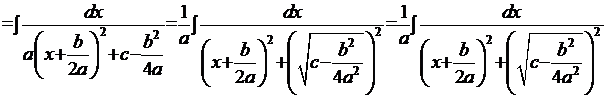
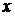 этого интеграла соответствует переменная
этого интеграла соответствует переменная  , а множителю
, а множителю  соответствует радикал:
соответствует радикал: 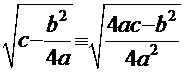
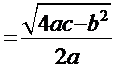 . Далее
. Далее 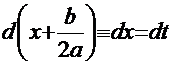 . Отсюда решение интеграла:
. Отсюда решение интеграла: 
 .
. . Это – табличный интеграл:
. Это – табличный интеграл: 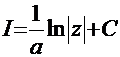 . Обратная подстановка
. Обратная подстановка  приводит к конечному результату:
приводит к конечному результату:  .
.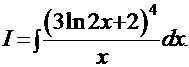
 ─ дифференциал функции
─ дифференциал функции 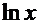 , а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену:
, а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену: 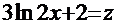 . Тогда
. Тогда 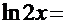


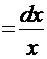
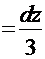 . В результате этой подстановки имеем табличный интеграл:
. В результате этой подстановки имеем табличный интеграл: 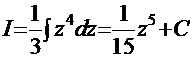 . Обратная подстановка приводит к конечному результату
. Обратная подстановка приводит к конечному результату 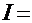
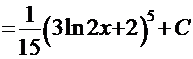 .
.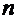 ой степени
ой степени 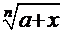 , т.е. компоненты типа
, т.е. компоненты типа 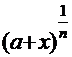 . Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
. Очевидно, такой радикал надо заменить какой-либо переменной того же типа.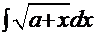 .
.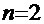 . Очевидна замена
. Очевидна замена 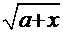 =
= 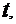 тогда
тогда 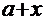 =
= 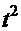
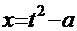
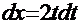 . Тогда интеграл легко приводится к
. Тогда интеграл легко приводится к 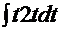 = =
= = 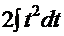
 +С.
+С. =
= 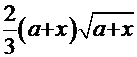 +С.
+С.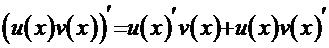 [1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций:
[1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций: 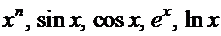 и их вариаций.
и их вариаций.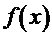 можно представить в виде произведения
можно представить в виде произведения 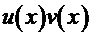 , то сочетание
, то сочетание 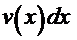 или
или  можно принять за дифференциал
можно принять за дифференциал 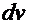 или
или 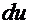 . Тогда решение интеграла получается по формуле:
. Тогда решение интеграла получается по формуле: 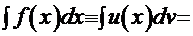

 .
.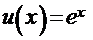 и
и 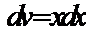 , либо
, либо 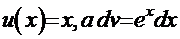 . Попробуем пойти первым путём
. Попробуем пойти первым путём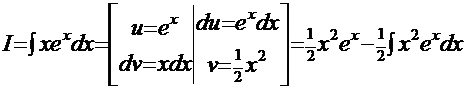 . Повторно применяем этот же метод:
. Повторно применяем этот же метод:  и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции
и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции 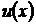 .
.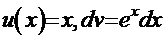 . Тогда
. Тогда 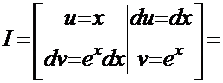
 .
.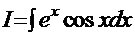 .
.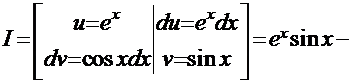
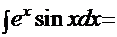


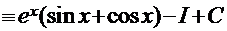
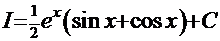 .
.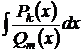 , где
, где  , а
, а 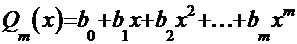 ─ полиномы порядка
─ полиномы порядка 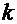 и
и  , соответственно.
, соответственно. . В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов:
. В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов: 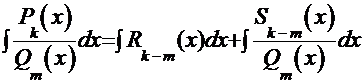 , где
, где 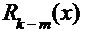
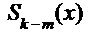 ─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;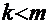 . Здесь сразу берётся интеграл указанным выше методом.
. Здесь сразу берётся интеграл указанным выше методом.


