

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Известно [1], что любой полином 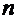 го порядка (n≥2) можно представить в виде произведения:
го порядка (n≥2) можно представить в виде произведения:
1 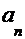 (коэффициента при старшей степени полинома);
(коэффициента при старшей степени полинома);
2 двучленов типа  ;
;
3 и трёхчленов типа 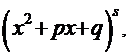
где  - действительные числа, (причём
- действительные числа, (причём 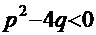 ),
), 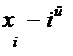 действительный корень полинома
действительный корень полинома 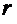 и
и 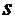 - кратности соответствующих сомножителей, при условии, что
- кратности соответствующих сомножителей, при условии, что 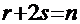 . По отношению к полиному знаменателя
. По отношению к полиному знаменателя 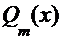 это означает, что подынтегральную функцию можно представить в виде суммы дробей типа
это означает, что подынтегральную функцию можно представить в виде суммы дробей типа  и
и 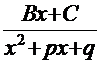 (
( и
и 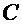 - некие числовые коэффициенты) с соответствующими кратностями (повторами корней). Тогда нахождение интеграла от рациональной дроби сведётся к взятию табличного интеграла типа
- некие числовые коэффициенты) с соответствующими кратностями (повторами корней). Тогда нахождение интеграла от рациональной дроби сведётся к взятию табличного интеграла типа  и интеграла типа
и интеграла типа 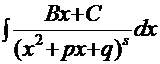 , способ решения которого для
, способ решения которого для 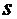 =1 рассмотрен в Примере 2. Остаётся только освоить методику разложения рациональной дроби на соответствующие слагаемые.
=1 рассмотрен в Примере 2. Остаётся только освоить методику разложения рациональной дроби на соответствующие слагаемые.
Рассмотрим несколько примеров на эту тему.
Пример 9. 
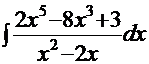 .
.
Рецепт. Здесь порядок полинома числителя больше порядка полинома знаменателя, поэтому делим «столбиком» числитель на знаменатель:
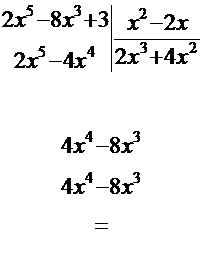
Таким образом, 
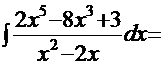
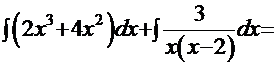
 , где
, где 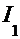 = =
= = 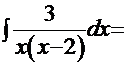
 . Здесь
. Здесь  действительные числа, которые подбираются следующим образом:
действительные числа, которые подбираются следующим образом:
1 сложим дроби: 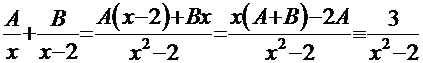 ;
;
2 затем приравняем коэффициенты при соответствующих степенях аргумента и получим систему двух линейных уравнений для  и
и 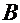 :
: 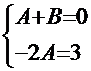 ;
;
тогда решение этой системы: 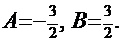
Отсюда интеграл  .
.
Таким образом, общее решение можно представить в следующем виде 
 .
.
Пример 10. 
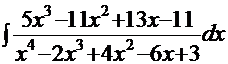 .
.
Рецепт.
1. Здесь порядок полинома числителя меньше порядка полинома знаменателя, поэтому не нужно выделять целую часть.
2. В предположении, что данный интеграл можно решить методом неопределённых коэффициентов, попробуем разложить полином знаменателя на множители.
Согласно теореме Виета, свободный член любого полинома равен произведению всех его корней на множитель 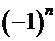 , где
, где 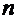 – порядок полинома. Здесь
– порядок полинома. Здесь  , тогда этот множитель равен единице. Попробуем подобрать хотя бы один целый корень, возьмём, например,
, тогда этот множитель равен единице. Попробуем подобрать хотя бы один целый корень, возьмём, например, 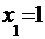 . При
. При 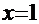 значение полинома: 1-2+4-6+3=0, т.е.
значение полинома: 1-2+4-6+3=0, т.е. 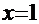 – один из корней. Теперь поделим исходный полином «столбиком» (см. выше) на двучлен
– один из корней. Теперь поделим исходный полином «столбиком» (см. выше) на двучлен  и получим полином третьего порядка
и получим полином третьего порядка 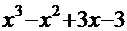 . Сгруппируем соответствующие слагаемые:
. Сгруппируем соответствующие слагаемые: 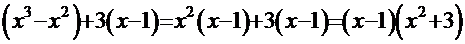 . Таким образом, подынтегральная функция должна иметь вид
. Таким образом, подынтегральная функция должна иметь вид 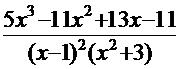 . В знаменателе имеется двучлен
. В знаменателе имеется двучлен  кратности 2 и «усечённый» трёхчлен
кратности 2 и «усечённый» трёхчлен 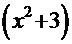 с отрицательным дискриминантом. В этом случае подынтегральную функцию можно представить в виде суммы дробей:
с отрицательным дискриминантом. В этом случае подынтегральную функцию можно представить в виде суммы дробей: 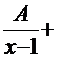
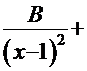
|
|
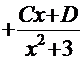 (здесь, как и раньше коэффициенты
(здесь, как и раньше коэффициенты 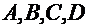 - действительные числа).
- действительные числа).
Обратите, пожалуйста, внимание на тот факт, что порядок полиномов в числителях этих дробей ровно на единицу меньше порядка полиномов в их знаменателях!
В результате сложения этих дробей получаем дробь: 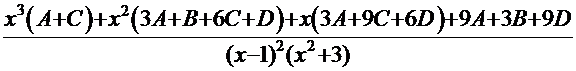 , числитель которой должен в точности совпадать с числителем дроби исходной подынтегральной функции. Это позволяет сформировать систему теперь уже четырёх линейных уравнений для этих коэффициентов:
, числитель которой должен в точности совпадать с числителем дроби исходной подынтегральной функции. Это позволяет сформировать систему теперь уже четырёх линейных уравнений для этих коэффициентов: 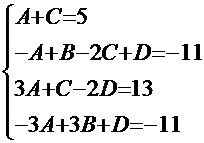 .
.
Нетрудно показать, что решение этой системы: 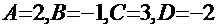 и исходный интеграл равен сумме трёх интегралов:
и исходный интеграл равен сумме трёх интегралов: 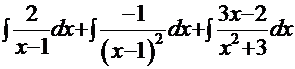 . Первые два – табличные и их результат:
. Первые два – табличные и их результат: 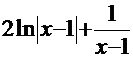 . Решение последнего интеграла:
. Решение последнего интеграла: 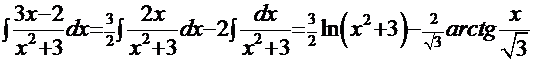 . Итак, ответ:
. Итак, ответ:

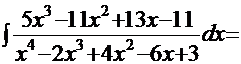
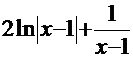
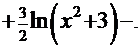
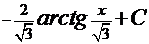
Обратите внимание на то, что громоздкий интеграл был сведён к комбинации табличных интегралов (решение последнего интеграла – см. Пример 3).
Пример 11.  .
.
Рецепт. Покажем, что этот интеграл можно достаточно просто решить тем же методом «неопределённых коэффициентов». Для этого домножим числитель и знаменатель на 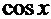 . Подынтегральная функция примет вид
. Подынтегральная функция примет вид 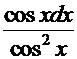 . Опытный взгляд сразу увидит в числителе дифференциал функции
. Опытный взгляд сразу увидит в числителе дифференциал функции  . Отсюда возникает желание ввести замену:
. Отсюда возникает желание ввести замену: 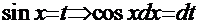 . Далее подставляем эти выражения в подынтегральную функцию, и интеграл приобретает следующий вид:
. Далее подставляем эти выражения в подынтегральную функцию, и интеграл приобретает следующий вид:  и готов к приложению к нему метода «неопределённых коэффициентов»:
и готов к приложению к нему метода «неопределённых коэффициентов»: 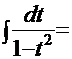
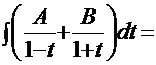
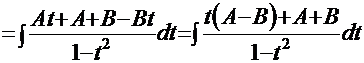 . Знакомым уже способом получаем систему уравнений:
. Знакомым уже способом получаем систему уравнений: 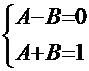 . Из решения системы следует:
. Из решения системы следует: 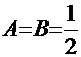 и
и  . После обратной подстановки
. После обратной подстановки 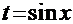 получаем окончательный результат:
получаем окончательный результат: 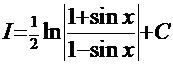 .
.
|
|
Это очень полезный результат, поэтому есть смысл записать его в дополнительную таблицу неопределённых интегралов (см. табл.2).
Легко показать, что аналогичный интеграл 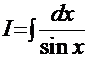 =
= 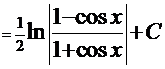 . С учётом формул
. С учётом формул  и
и 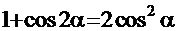 получаем ещё один вариант решения этого интеграла:
получаем ещё один вариант решения этого интеграла: 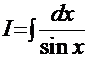 =
=  +С. И этот результат рекомендуем внести в ту же дополнительную таблицу.
+С. И этот результат рекомендуем внести в ту же дополнительную таблицу.
|
|
|

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!