Часто в состав подынтегральных функций входят радикалы трёх видов: 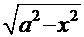 ,
, 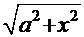 и
и 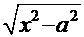 . В этих случаях применяются соответствующие так называемые «тригонометрические» подстановки:
. В этих случаях применяются соответствующие так называемые «тригонометрические» подстановки:
1. Для 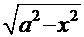 -
- 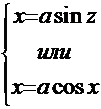

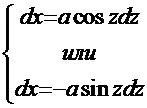 , соответственно.
, соответственно.
Рассмотрим применение этой рекомендации на конкретном примере.
Пример 21. 
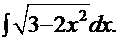
Рецепт. Преобразуем подынтегральную функцию 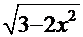 =
= 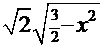 и замещаем аргумент
и замещаем аргумент 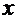 по одному из двух вариантов (см. выше), например,
по одному из двух вариантов (см. выше), например, 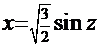 , тогда
, тогда 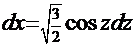 . В итоге
. В итоге 
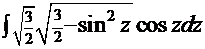 =
= 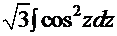 =
= 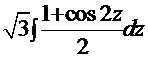 =
= 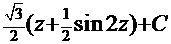 . Обратная постановка:
. Обратная постановка: 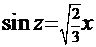 ,
, 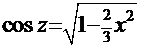 =
= 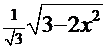 и
и 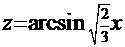 даёт конечный результат
даёт конечный результат 
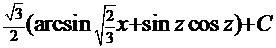 =
= 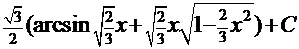 =
=  +
+ 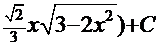 .
.
2. Для 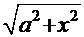 -
- 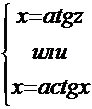

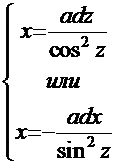 . Дальше следует решение примера на эту тему.
. Дальше следует решение примера на эту тему.
Пример 22. 
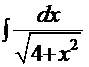 .
.
Рецепт. Здесь 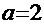 , поэтому применим вариант замены из двух предложенных выше, например,
, поэтому применим вариант замены из двух предложенных выше, например, 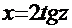

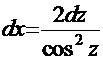

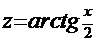 .
.

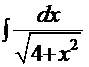 =
= 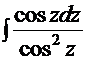 =
= 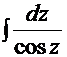 . Это уже знакомый интеграл (см. Пример 11), тогда
. Это уже знакомый интеграл (см. Пример 11), тогда 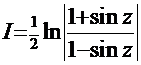 +С. Нетрудно показать, что
+С. Нетрудно показать, что 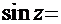
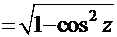 =
= 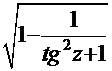 =
= 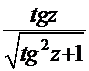 . После обратной подстановки
. После обратной подстановки 
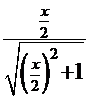 =
= 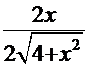 =
= 
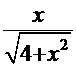 .
.
Итак, имеем конечный результат: 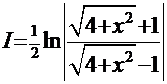 +С.
+С.
3. Для 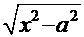 -
- 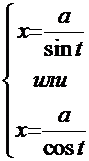

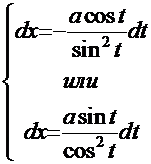 . Решим соответствующий пример.
. Решим соответствующий пример.
Пример 23. 
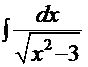 .
.
Рецепт. Здесь 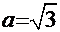 . Согласно рекомендациям выберем, например, вариант
. Согласно рекомендациям выберем, например, вариант 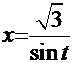

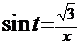

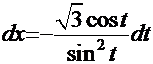 . Тогда искомый интеграл
. Тогда искомый интеграл 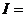
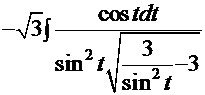 =
= 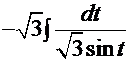 =
= 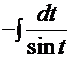 . Это интеграл, рассмотренный ранее, тогда промежуточное решение имеет вид:
. Это интеграл, рассмотренный ранее, тогда промежуточное решение имеет вид: 
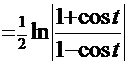 +С. Обратная подстановка даёт окончательное решение
+С. Обратная подстановка даёт окончательное решение 
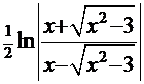 +С.
+С.
8. Интегралы с иррациональностью типа 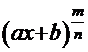 .
.
Рассмотрим один из вариантов таких интегралов на примере интеграла  =
= 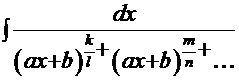 ., где k, m, … – любые целые числа,
., где k, m, … – любые целые числа, 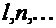 =1,2,…,
=1,2,…, 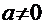 .
.
Алгоритм решения интегралов такого типа:
1 необходимо найти целое число М – наименьшее общее кратное (НОК) чисел 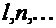 ;
;
2 дроби 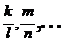 заменить соответствующими им дробями
заменить соответствующими им дробями 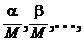 где
где 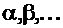 ─ целые числа;
─ целые числа;
3 тогда знаменатель подынтегральной функции принимает вид 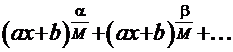
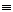
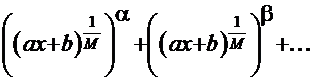 ;
;
4 теперь следует очевидная замена: 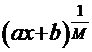 =
= 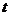 , отсюда
, отсюда 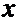 =
= 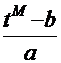 и
и 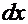 =
= 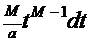 .
.
Далее,  =
= 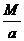
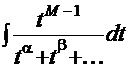 , а этот интеграл решается по образцу Примера 9 или Примера 10
, а этот интеграл решается по образцу Примера 9 или Примера 10
Пример 24.  =
= 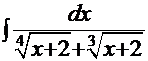
Рецепт. При сопоставлении данного примера с вышеприведённым получаем (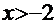 ):
):
1 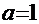 ,
, 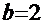 ,
, 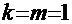 ,
, 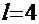 ,
, 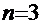 .
.
2 НОК (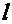 ,
, 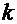 ) = М=12;
) = М=12;
3 замена 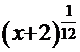 =
= 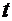 ,
, 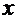 =
= 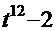 ,
, 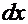 =
= 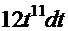 ;
;
4 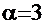 ,
, 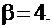
Интеграл преобразуется: 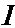 =
= 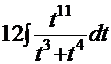 =
= 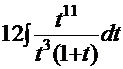 =
= 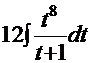 . Здесь полная аналогия Примера 9:
. Здесь полная аналогия Примера 9: 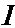 =
= 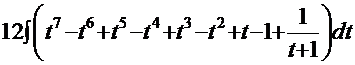 =12
=12 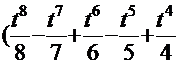 -
- 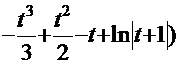 =
= 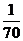
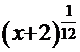
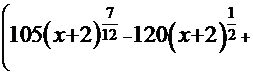
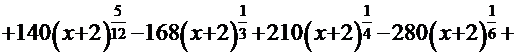
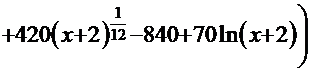 +С.
+С.
Таблица 2
Дополнительная таблица интегралов, полученных
в результате промежуточных расчётов
Образец решения расчётно-графической работы
Решение любого варианта РГР рассмотрим на примере «нулевого» варианта
Таблица 3
«Нулевой» вариант РГР
| Номер задания
| Интегралы
|
|
0
| 1. 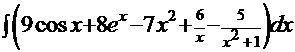 2. 2. 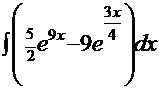 3. 3. 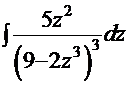 4. 4. 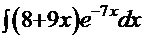 5. 5. 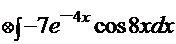 6. 6. 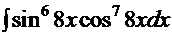 7. 7. 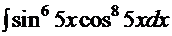 8. 8. 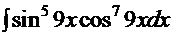 9. 9. 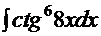 10. 10. 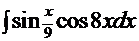 11. 11. 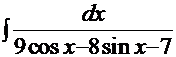 12. 12. 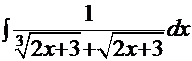 13. 13. 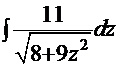 14. 14. 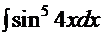
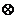 - решение данного интеграла сопроводить совмещённым графиком функций - решение данного интеграла сопроводить совмещённым графиком функций 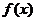 и и 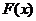
|
Примечания
1. Все 25 заданий приводятся в ПРИЛОЖЕНИИ 1.
2. Выполнение каждой задачи данного демонстрационного варианта должен сопровождаться проверкой решения (см. образец).
1.  =
= 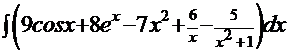 . Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем:
. Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем:  =
= 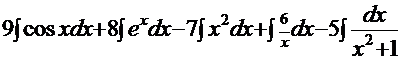 , а это – табличные интегралы, поэтому решение:
, а это – табличные интегралы, поэтому решение:  =
= 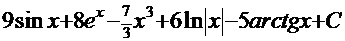 .
.
ПРОВЕРКА 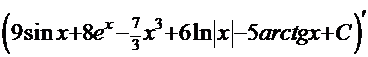 =
= 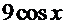 +
+ 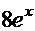 ─
─ 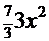 +
+ 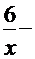
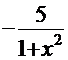 =
= 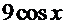 +
+ 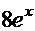
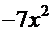 +
+ 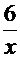
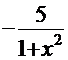 . Получено полное совпадение с подынтегральной функцией решаемого интеграла, значит, решение - верное.
. Получено полное совпадение с подынтегральной функцией решаемого интеграла, значит, решение - верное.
Ответ  =
= 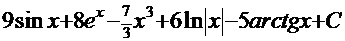 .
.
2.  =
= 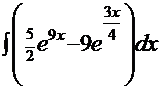 =
= 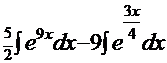 =
= 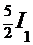
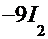 . Для решения обоих интегралов используем приём «замены переменных»:
. Для решения обоих интегралов используем приём «замены переменных»: 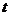 =
= 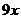 для интеграла
для интеграла 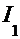 и
и 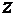 =
= 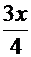 - для интеграла
- для интеграла 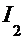 . Тогда
. Тогда 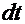 =
= 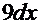

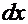 =
= 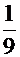
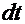 . Получаем
. Получаем 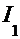 =
= 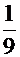
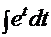 (табличный интеграл)=
(табличный интеграл)= 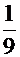
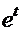 . С помощью обратной подстановки получаем
. С помощью обратной подстановки получаем 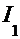 =
= 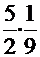
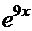 =
= 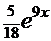 .
.
Аналогичные преобразования для интеграла 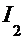 :
: 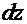 =
= 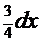

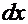 =
= 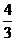
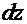 приводят к результату
приводят к результату 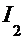 =
= 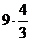
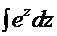 =
= 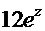 =
= 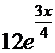 . Таким образом, общее решение
. Таким образом, общее решение  =
= 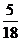
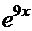
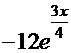 +С.
+С.
ПРОВЕРКА (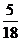
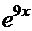
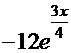 +С)
+С)  =
= 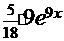
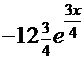 =
= 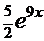
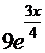 ─ очевидное совпадение.
─ очевидное совпадение.
Ответ:  =
= 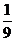
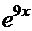 +
+ 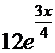 +С.
+С.
3.  =
= 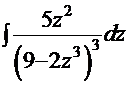 . Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»:
. Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»: 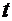 =
= 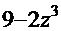 . Тогда дифференциал
. Тогда дифференциал 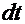 =
= 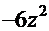
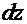

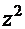
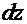 =
= 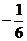
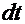 и интеграл принимает вид
и интеграл принимает вид 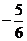
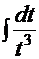 , т.е. снова табличный интеграл
, т.е. снова табличный интеграл 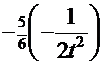 =
= 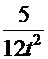 . После обратной замены получаем
. После обратной замены получаем  =
= 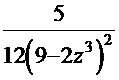 .
.
ПРОВЕРКА: 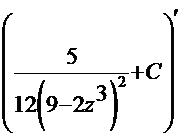 =
= 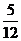
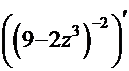 =
= 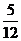
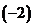
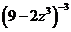
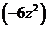 =
=
= 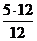
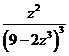 =
= 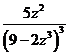 - снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
- снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
Ответ  =
= 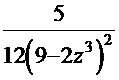 +С.
+С.
4.  =
= 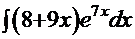 . Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»:
. Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»: 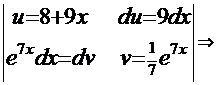
 =
= 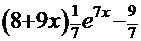
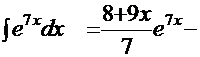
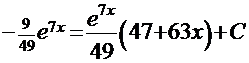 .
.
ПРОВЕРКА 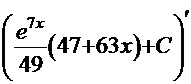 =
= 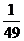
 =
= 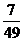
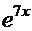
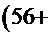
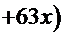 =
= 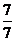
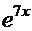
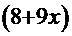 =
= 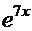
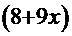 ─ интеграл взят верно.
─ интеграл взят верно.
Ответ  =
= 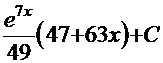 .
.
5.  =
= 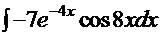 . Сравнение этого интеграла с интегралом Примера 8 снова вызывает ассоциации с тем же методом «по частям»:
. Сравнение этого интеграла с интегралом Примера 8 снова вызывает ассоциации с тем же методом «по частям»:  =
= 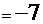
 =
= 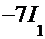 , т.е.
, т.е. 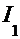 =
=  . Тогда вводим
. Тогда вводим
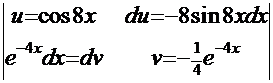

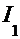 =
= 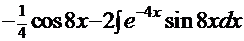 . Снова применим метод «по частям», но уже к вторичному интегралу:
. Снова применим метод «по частям», но уже к вторичному интегралу: 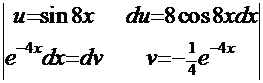 . Продолжим интегрирование:
. Продолжим интегрирование: 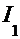 =
= 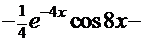
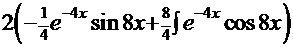 = =
= = 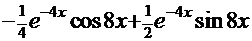
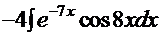 . Но последний интеграл совпадает с исходным интегралом, отсюда получаем следующее равенство
. Но последний интеграл совпадает с исходным интегралом, отсюда получаем следующее равенство 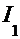 =
= 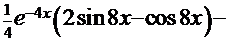
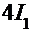 . Тогда 5
. Тогда 5 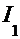 =
= 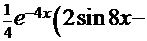
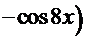 ,
, 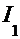 =
=  а искомый интеграл ─
а искомый интеграл ─  =
= 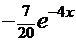
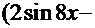
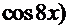 +С.
+С.
Согласно тексту задания в данном пункте необходимо построить вместе графики подынтегральной и первообразной функции 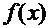 и
и 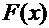 , чтобы визуально убедиться в выполнении основного свойства неопределённого интеграла:
, чтобы визуально убедиться в выполнении основного свойства неопределённого интеграла: 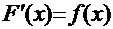 . Выбор интервала значений аргумента
. Выбор интервала значений аргумента 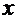 в общем случае – любой, хотя определённый интерес, например, может представлять анализ поведения этих функций вблизи точек экстремума первообразной функции, т.е. вблизи корней уравнения
в общем случае – любой, хотя определённый интерес, например, может представлять анализ поведения этих функций вблизи точек экстремума первообразной функции, т.е. вблизи корней уравнения 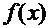 =0. Из текста решения данного интеграла следует, что подынтегральная функция
=0. Из текста решения данного интеграла следует, что подынтегральная функция 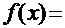
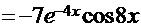 , а первообразная функция (решение интеграла)
, а первообразная функция (решение интеграла) 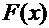 =
= 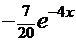
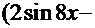
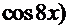 +С. Решаем уравнение:
+С. Решаем уравнение: 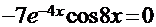

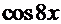 =0. Нетрудно убедиться, что это уравнение имеет бесконечное множество решений:
=0. Нетрудно убедиться, что это уравнение имеет бесконечное множество решений: 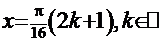 . При
. При 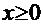 значения обеих функций быстро уменьшаются из-за множителя
значения обеих функций быстро уменьшаются из-за множителя 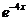 , а при
, а при 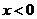 наоборот устремляются к
наоборот устремляются к 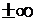 , соответственно. Поэтому имеет смысл выбрать, например, интервал
, соответственно. Поэтому имеет смысл выбрать, например, интервал 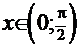 . Найдём корни, принадлежащие этому интервалу:
. Найдём корни, принадлежащие этому интервалу: 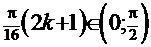

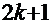
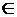
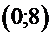

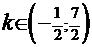 . Поскольку
. Поскольку 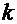 ─ целое число, то эта величина в данном интервале может принять только четыре разных значения: 0,1,2 и 3, что соответствует четырём корням:
─ целое число, то эта величина в данном интервале может принять только четыре разных значения: 0,1,2 и 3, что соответствует четырём корням: 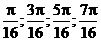 . Построить совмещённый график Вы можете двумя способами: вручную или средствами Excel. Но в любом случае необходимо иметь таблицу, содержащую исходные данные и поэтому состоящую из трёх колонок. Первая ─ набор значений аргумента
. Построить совмещённый график Вы можете двумя способами: вручную или средствами Excel. Но в любом случае необходимо иметь таблицу, содержащую исходные данные и поэтому состоящую из трёх колонок. Первая ─ набор значений аргумента 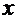 , две остальных ─ значения подынтегральной функции
, две остальных ─ значения подынтегральной функции 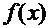 и первообразной функции
и первообразной функции 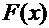 для соответствующих значений
для соответствующих значений 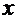 . Алгоритм создания этой таблицы приведён в Приложении 2. Там же показано, как можно построить необходимый график на базе этой таблицы средствами Excel. В последнем случае построенный в Excel график можно распечатать на принтере и вклеить в отчёт (рис.1).
. Алгоритм создания этой таблицы приведён в Приложении 2. Там же показано, как можно построить необходимый график на базе этой таблицы средствами Excel. В последнем случае построенный в Excel график можно распечатать на принтере и вклеить в отчёт (рис.1).
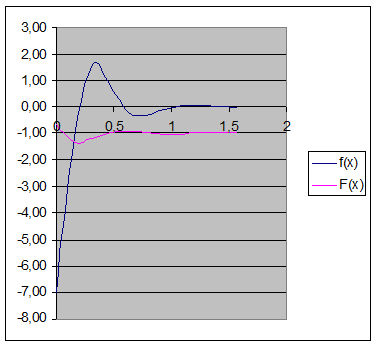
Рис.1. Графики подынтегральной 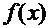 и первообразной
и первообразной  функций, соответственно, построенных средствами Excel.
функций, соответственно, построенных средствами Excel.
Эти графики построены с использованием табл.4.
Таблица 4
Значения подынтегральной 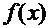 и первообразной функций
и первообразной функций 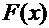 .
.
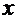
| 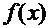
| 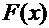
|
| 0
| -7,00
| -0,65
|
| 0,16
| -1,15
| -1,30
|
| 0,31
| 1,61
| -1,20
|
| 0,47
| 0,86
| -0,98
|
| 0,63
| -0,18
| -0,94
|
| 0,79
| -0,30
| -0,98
|
| 0,94
| -0,05
| -1,01
|
| 1,10
| 0,07
| -1,01
|
| 1,26
| 0,04
| -1,00
|
| 1,41
| -0,01
| -1,00
|
| 1,57
| -0,01
| -1,00
|
Табл.4.Исходные данные: 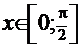 , подынтегральная функция
, подынтегральная функция 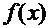 и первообразная функция
и первообразная функция 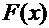 .
.
А теперь тот же рисунок, но выполнений от руки на базе той же таблицы (рис.2).
Рис.2. Графики подынтегральной 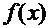 и первообразной
и первообразной 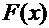 функций, соответственно, построенные вручную.
функций, соответственно, построенные вручную.
Хорошо видно, что на обоих рисунках нулям подынтегральной функции 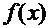 в точности соответствуют точки экстремумов первообразной функции
в точности соответствуют точки экстремумов первообразной функции 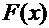 , т.е. имеет место наглядное подтверждение свойства
, т.е. имеет место наглядное подтверждение свойства 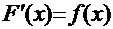 .
.
Естественно, что вы должны оформить любой из этих рисунков на ваш выбор.
ПРОВЕРКА: 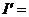
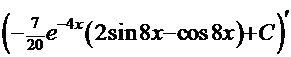 =
= 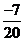
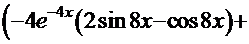
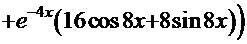 =
= 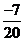
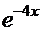
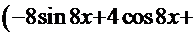
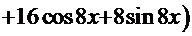 =
= 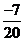
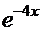
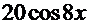 =
= 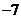
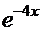
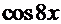 ч.т.д.
ч.т.д.
Ответ:  =.
=.  +С.
+С.
6.  =
= 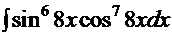 . Согласно рекомендациям на с.13─14 проводим замену функции
. Согласно рекомендациям на с.13─14 проводим замену функции 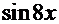 на функцию
на функцию 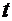

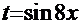

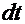 =
= 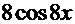
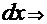

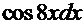 =
= 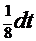 . Тогда искомый интеграл получит вид
. Тогда искомый интеграл получит вид  =
= 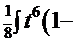
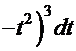 =
= 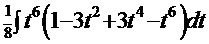 =
= 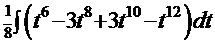 . Поэтому в соответствии со свойством 4 с.5 («интеграл суммы функций» равен «сумме интегралов») с использованием табличного интеграла
. Поэтому в соответствии со свойством 4 с.5 («интеграл суммы функций» равен «сумме интегралов») с использованием табличного интеграла 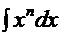 получаем
получаем  =
= 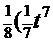 ─
─ 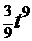 +
+ 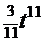
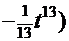 =
= 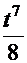 (
(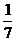
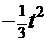 +
+ 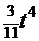 -
- 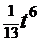 ). После обратной подстановки
). После обратной подстановки 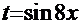 получаем:
получаем:  =
= 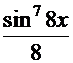 (
(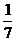
 +
+ 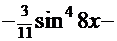
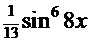 ) + С. Кстати сказать, с аналогичным интегралом можно познакомиться в Примере 14.
) + С. Кстати сказать, с аналогичным интегралом можно познакомиться в Примере 14.
ПРОВЕРКА (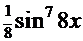 (
(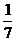 ─
─ 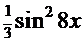 +
+ 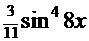
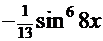 )+С)
)+С)  =
= 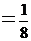
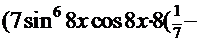
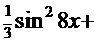
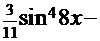
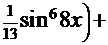 +
+ 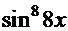 (
( +
+ 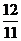
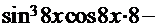
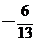
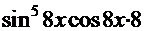 ))=
))= 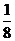
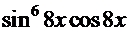 (
(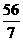 ─
─ 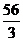
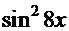 +
+ 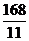
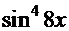 ─
─
─ 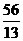
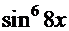 ─
─ 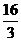
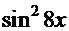 +
+ 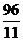
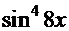 ─
─ 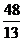
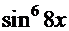 )=
)= 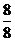
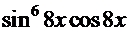 (1─
(1─ 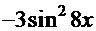
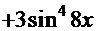
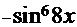 ). Используя основное тригонометрическое тождество
). Используя основное тригонометрическое тождество  , переписываем полученное выражение:
, переписываем полученное выражение: 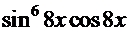 (1─3
(1─3 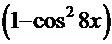 +3
+3 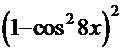
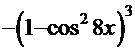 ). Дальнейшие преобразования в скобках дают конечный результат:
). Дальнейшие преобразования в скобках дают конечный результат: 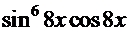 , подтверждающий правильность решённого интеграла.
, подтверждающий правильность решённого интеграла.
Отве т:  =
= 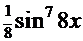 (
(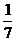
 +
+ 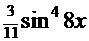
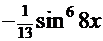 )+С.
)+С.
7.  =
= 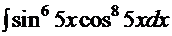 . Воспользовавшись известными тригонометрическими формулами
. Воспользовавшись известными тригонометрическими формулами 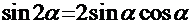 и
и 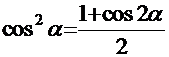 , преобразуем подынтегральную функцию и получаем:
, преобразуем подынтегральную функцию и получаем:  =
= 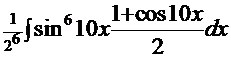 =
= 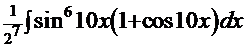 =
= 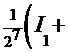
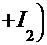 +С, где
+С, где 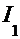 =
= 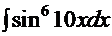 , а
, а 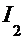 =
= 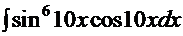 .
.
Сначала с помощью формулы 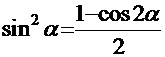 решаем первый
решаем первый
интеграл 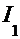 =
= 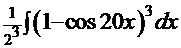 =
= 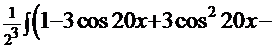
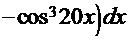
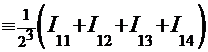 , где
, где
1 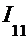 =
= 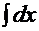 =
= 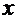 ;
;
2 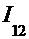 =
= 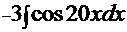 =(снова замена аргумента)=
=(снова замена аргумента)= 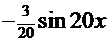 ;
;
3 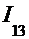 =
= 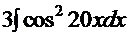 =(удвоение аргумента)=
=(удвоение аргумента)= 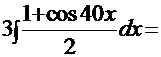 =
= 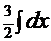 +
+ 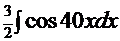
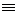
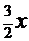 +
+  ;
;
4 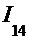 =
= 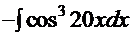 =
= 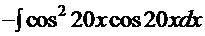 =
= 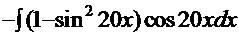 =(уже знакомым приёмом
=(уже знакомым приёмом 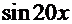 =
= 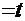

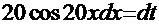

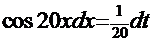 )=
)= 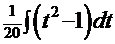 =
= 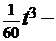
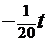 .
.
После обратной замены 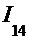 =
= 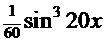
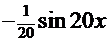 .
.
Возвращаемся к первому интегралу: 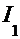 =
= 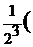
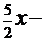
 +
+ 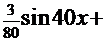 +
+ 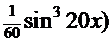 .
.
Второй интеграл решаем с помощью аналогичной замены: 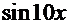 =
= 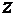
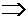
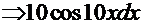 =
= 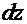

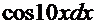 =
= 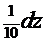 .
. 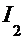 =
= 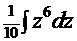 =
= 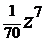 . После обратной замены
. После обратной замены 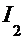 =
= 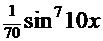 .
.
Собрав вместе результаты расчётов, получаем конечный результат:
 =
= 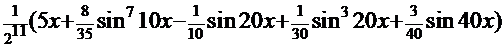 +С.
+С.
Авторы приносят извинения, но в виду того, что проверочные преобразования данной задачи оказались чрезвычайно громоздкими, мы не приводим подробно проверку! Желающие могут попробовать сделать это самостоятельно.
Ответ:  =
= 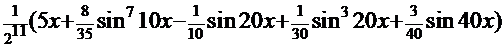 +С.
+С.
8.  =
= 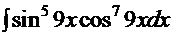 . В этом интеграле подынтегральная функция (см. с. 16) последовательно преобразуется к форме, содержащей только степени функции
. В этом интеграле подынтегральная функция (см. с. 16) последовательно преобразуется к форме, содержащей только степени функции 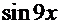 и её дифференциал:
и её дифференциал: 
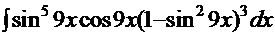 . Воспользовавшись формулой
. Воспользовавшись формулой 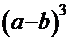 =
= 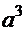
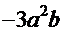 +
+ 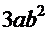
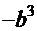 и введя замену
и введя замену 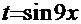
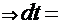
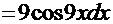

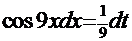 , получаем интеграл
, получаем интеграл 
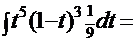 =
= 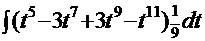 . Этот интеграл легко решается:
. Этот интеграл легко решается: 
= 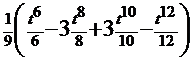 +С=
+С= 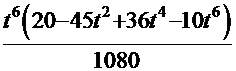 +С.
+С.
После обратной подстановки получаем  =
= 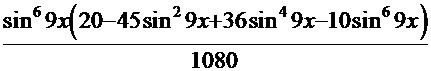 +С.
+С.
N.B.! Этот алгоритм, естественно, не единственный: можно было бы сделать замену 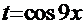 или
или 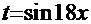 и др.
и др.
ПРОВЕРКА
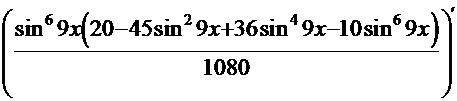 =
=
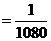
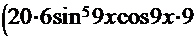 ─
─ 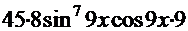 +
+
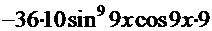
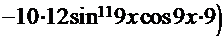 =
=
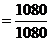
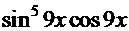
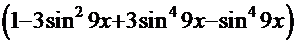 =
=
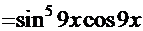
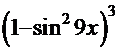 =
= 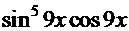
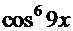 =
=
= 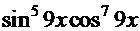 ─ правильность решения подтверждена.
─ правильность решения подтверждена.
Ответ: 
|
|
|



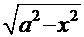 ,
, 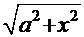 и
и 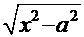 . В этих случаях применяются соответствующие так называемые «тригонометрические» подстановки:
. В этих случаях применяются соответствующие так называемые «тригонометрические» подстановки: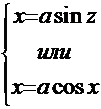

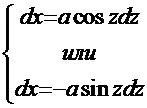 , соответственно.
, соответственно.
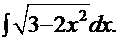
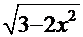 =
= 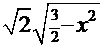 и замещаем аргумент
и замещаем аргумент 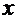 по одному из двух вариантов (см. выше), например,
по одному из двух вариантов (см. выше), например, 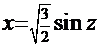 , тогда
, тогда 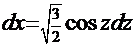 . В итоге
. В итоге 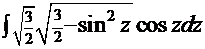 =
= 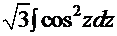 =
= 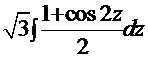 =
= 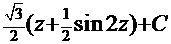 . Обратная постановка:
. Обратная постановка: 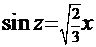 ,
, 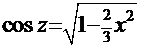 =
= 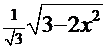 и
и 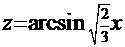 даёт конечный результат
даёт конечный результат 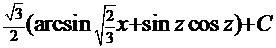 =
= 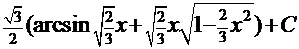 =
=  +
+ 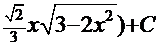 .
.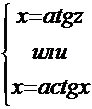
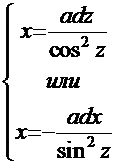 . Дальше следует решение примера на эту тему.
. Дальше следует решение примера на эту тему.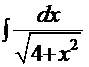 .
.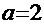 , поэтому применим вариант замены из двух предложенных выше, например,
, поэтому применим вариант замены из двух предложенных выше, например, 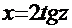
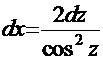
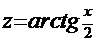 .
.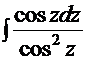 =
= 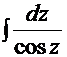 . Это уже знакомый интеграл (см. Пример 11), тогда
. Это уже знакомый интеграл (см. Пример 11), тогда 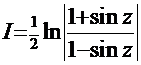 +С. Нетрудно показать, что
+С. Нетрудно показать, что 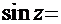
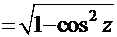 =
= 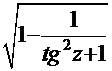 =
= 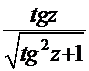 . После обратной подстановки
. После обратной подстановки 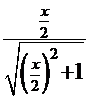 =
= 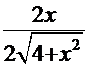 =
= 
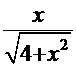 .
.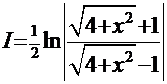 +С.
+С.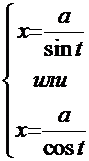
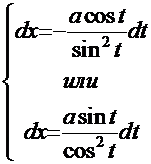 . Решим соответствующий пример.
. Решим соответствующий пример.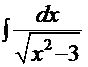 .
.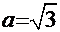 . Согласно рекомендациям выберем, например, вариант
. Согласно рекомендациям выберем, например, вариант 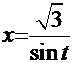
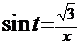
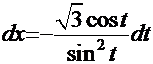 . Тогда искомый интеграл
. Тогда искомый интеграл 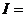
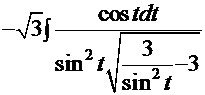 =
= 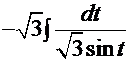 =
= 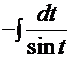 . Это интеграл, рассмотренный ранее, тогда промежуточное решение имеет вид:
. Это интеграл, рассмотренный ранее, тогда промежуточное решение имеет вид: 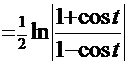 +С. Обратная подстановка даёт окончательное решение
+С. Обратная подстановка даёт окончательное решение 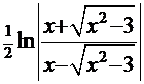 +С.
+С.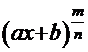 .
. =
= 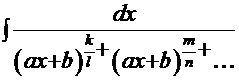 ., где k, m, … – любые целые числа,
., где k, m, … – любые целые числа, 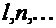 =1,2,…,
=1,2,…, 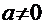 .
.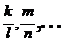 заменить соответствующими им дробями
заменить соответствующими им дробями 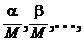 где
где 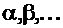 ─ целые числа;
─ целые числа;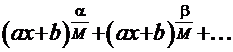
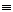
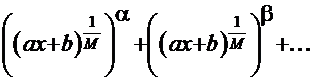 ;
;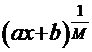 =
= 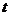 , отсюда
, отсюда 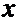 =
= 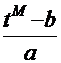 и
и 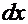 =
= 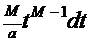 .
.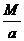
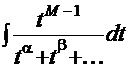 , а этот интеграл решается по образцу Примера 9 или Примера 10
, а этот интеграл решается по образцу Примера 9 или Примера 10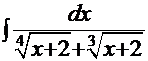
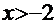 ):
):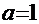 ,
, 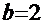 ,
, 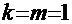 ,
, 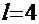 ,
, 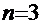 .
.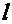 ,
, 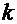 ) = М=12;
) = М=12;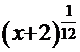 =
= 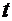 ,
, 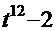 ,
, 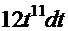 ;
;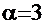 ,
, 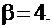
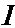 =
= 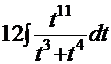 =
= 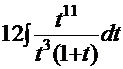 =
= 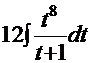 . Здесь полная аналогия Примера 9:
. Здесь полная аналогия Примера 9: 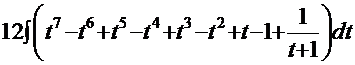 =12
=12 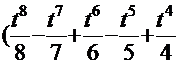 -
- 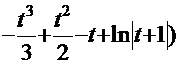 =
= 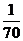
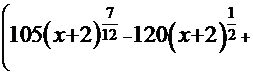
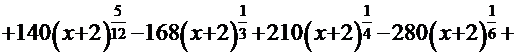
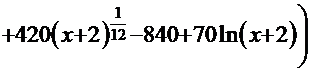 +С.
+С.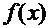
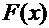
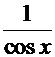
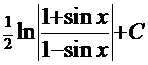 или
или 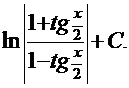
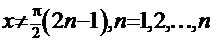
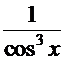
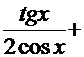
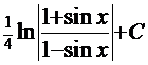
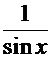
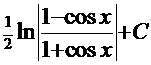 =
= 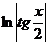 +С
+С
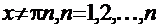
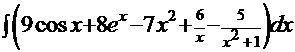 2.
2. 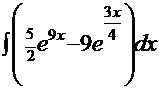 3.
3. 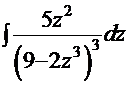 4.
4. 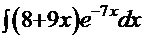 5.
5. 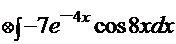 6.
6. 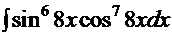 7.
7. 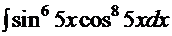 8.
8. 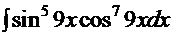 9.
9. 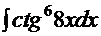 10.
10. 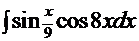 11.
11. 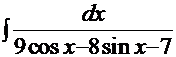 12.
12. 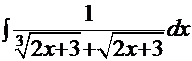 13.
13. 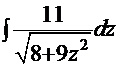 14.
14. 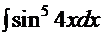
 - решение данного интеграла сопроводить совмещённым графиком функций
- решение данного интеграла сопроводить совмещённым графиком функций 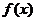 и
и 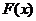
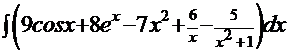 . Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем:
. Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем: 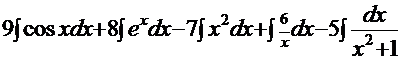 , а это – табличные интегралы, поэтому решение:
, а это – табличные интегралы, поэтому решение: 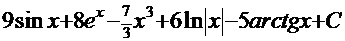 .
.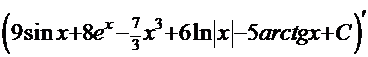 =
= 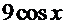 +
+ 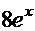 ─
─ 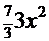 +
+ 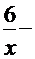
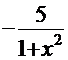 =
= 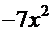 +
+ 
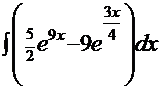 =
= 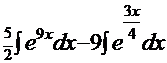 =
= 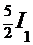
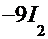 . Для решения обоих интегралов используем приём «замены переменных»:
. Для решения обоих интегралов используем приём «замены переменных»: 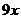 для интеграла
для интеграла 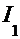 и
и 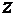 =
= 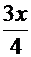 - для интеграла
- для интеграла 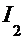 . Тогда
. Тогда 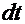 =
= 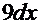
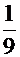
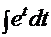 (табличный интеграл)=
(табличный интеграл)= 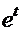 . С помощью обратной подстановки получаем
. С помощью обратной подстановки получаем 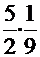
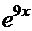 =
= 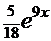 .
.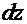 =
= 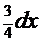
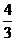
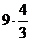
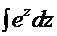 =
= 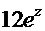 =
= 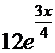 . Таким образом, общее решение
. Таким образом, общее решение 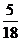
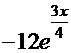 +С.
+С. =
= 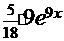
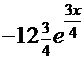 =
= 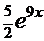
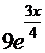 ─ очевидное совпадение.
─ очевидное совпадение.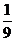
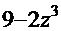 . Тогда дифференциал
. Тогда дифференциал 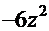
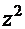
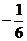
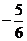
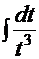 , т.е. снова табличный интеграл
, т.е. снова табличный интеграл 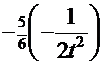 =
= 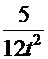 . После обратной замены получаем
. После обратной замены получаем 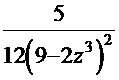 .
.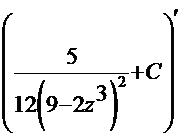 =
= 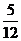
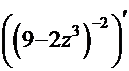 =
= 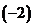
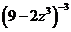
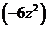 =
=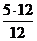
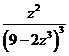 =
= 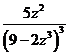 - снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
- снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.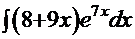 . Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»:
. Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»: 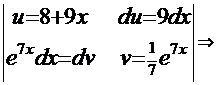
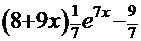
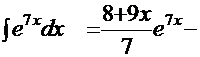
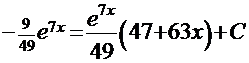 .
.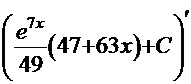 =
= 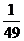
 =
= 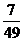
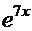
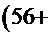
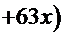 =
= 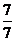
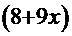 =
= 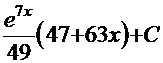 .
.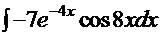 . Сравнение этого интеграла с интегралом Примера 8 снова вызывает ассоциации с тем же методом «по частям»:
. Сравнение этого интеграла с интегралом Примера 8 снова вызывает ассоциации с тем же методом «по частям»: 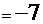
 =
= 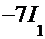 , т.е.
, т.е. 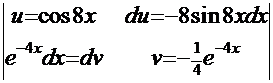
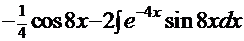 . Снова применим метод «по частям», но уже к вторичному интегралу:
. Снова применим метод «по частям», но уже к вторичному интегралу: 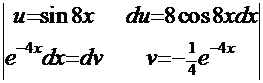 . Продолжим интегрирование:
. Продолжим интегрирование: 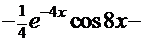
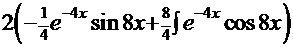 = =
= = 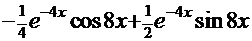
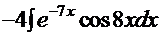 . Но последний интеграл совпадает с исходным интегралом, отсюда получаем следующее равенство
. Но последний интеграл совпадает с исходным интегралом, отсюда получаем следующее равенство 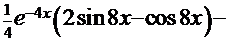
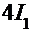 . Тогда 5
. Тогда 5 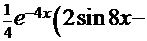
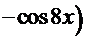 ,
,  а искомый интеграл ─
а искомый интеграл ─ 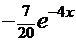
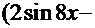
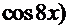 +С.
+С.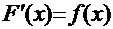 . Выбор интервала значений аргумента
. Выбор интервала значений аргумента 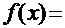
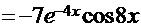 , а первообразная функция (решение интеграла)
, а первообразная функция (решение интеграла) 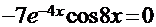
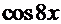 =0. Нетрудно убедиться, что это уравнение имеет бесконечное множество решений:
=0. Нетрудно убедиться, что это уравнение имеет бесконечное множество решений: 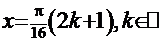 . При
. При 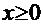 значения обеих функций быстро уменьшаются из-за множителя
значения обеих функций быстро уменьшаются из-за множителя 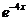 , а при
, а при 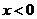 наоборот устремляются к
наоборот устремляются к 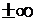 , соответственно. Поэтому имеет смысл выбрать, например, интервал
, соответственно. Поэтому имеет смысл выбрать, например, интервал 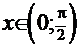 . Найдём корни, принадлежащие этому интервалу:
. Найдём корни, принадлежащие этому интервалу: 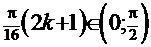
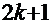
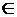
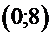
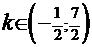 . Поскольку
. Поскольку 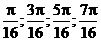 . Построить совмещённый график Вы можете двумя способами: вручную или средствами Excel. Но в любом случае необходимо иметь таблицу, содержащую исходные данные и поэтому состоящую из трёх колонок. Первая ─ набор значений аргумента
. Построить совмещённый график Вы можете двумя способами: вручную или средствами Excel. Но в любом случае необходимо иметь таблицу, содержащую исходные данные и поэтому состоящую из трёх колонок. Первая ─ набор значений аргумента 
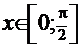 , подынтегральная функция
, подынтегральная функция 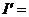
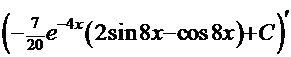 =
= 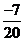
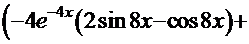
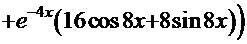 =
= 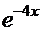
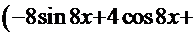
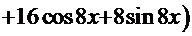 =
= 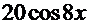 =
= 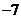
 +С.
+С.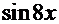 на функцию
на функцию 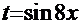
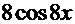
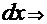
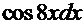 =
= 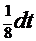 . Тогда искомый интеграл получит вид
. Тогда искомый интеграл получит вид 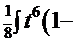
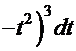 =
= 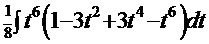 =
= 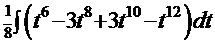 . Поэтому в соответствии со свойством 4 с.5 («интеграл суммы функций» равен «сумме интегралов») с использованием табличного интеграла
. Поэтому в соответствии со свойством 4 с.5 («интеграл суммы функций» равен «сумме интегралов») с использованием табличного интеграла 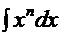 получаем
получаем 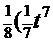 ─
─ 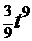 +
+ 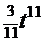
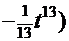 =
= 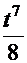 (
(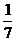
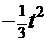 +
+ 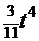 -
- 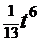 ). После обратной подстановки
). После обратной подстановки 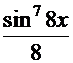 (
( +
+ 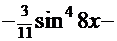
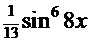 ) + С. Кстати сказать, с аналогичным интегралом можно познакомиться в Примере 14.
) + С. Кстати сказать, с аналогичным интегралом можно познакомиться в Примере 14.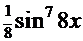 (
(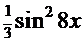 +
+ 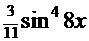
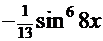 )+С)
)+С) 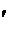 =
= 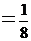
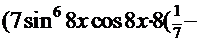
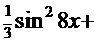
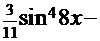
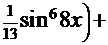 +
+ 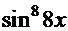 (
( +
+ 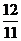
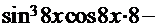
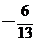
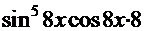 ))=
))= 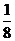
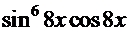 (
(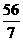 ─
─ 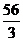
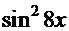 +
+ 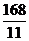
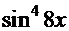 ─
─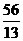
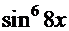 ─
─ 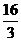
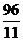
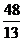
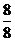
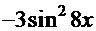
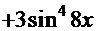
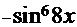 ). Используя основное тригонометрическое тождество
). Используя основное тригонометрическое тождество  , переписываем полученное выражение:
, переписываем полученное выражение: 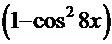 +3
+3 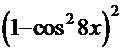
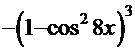 ). Дальнейшие преобразования в скобках дают конечный результат:
). Дальнейшие преобразования в скобках дают конечный результат: 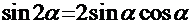 и
и 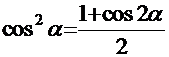 , преобразуем подынтегральную функцию и получаем:
, преобразуем подынтегральную функцию и получаем: 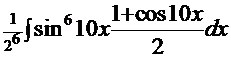 =
= 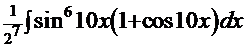 =
= 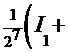
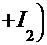 +С, где
+С, где 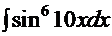 , а
, а 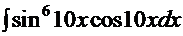 .
.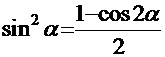 решаем первый
решаем первый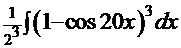 =
= 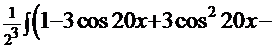
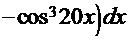
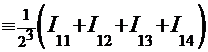 , где
, где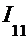 =
= 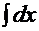 =
= 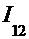 =
= 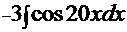 =(снова замена аргумента)=
=(снова замена аргумента)= 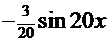 ;
;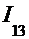 =
= 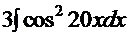 =(удвоение аргумента)=
=(удвоение аргумента)= 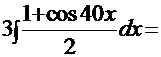 =
= 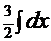 +
+ 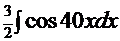
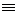
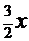 +
+  ;
;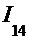 =
= 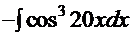 =
= 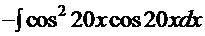 =
= 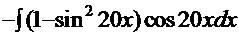 =(уже знакомым приёмом
=(уже знакомым приёмом 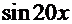 =
= 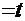
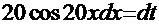
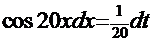 )=
)= 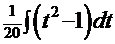 =
= 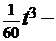
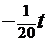 .
.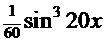
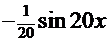 .
.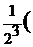
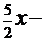
 +
+ 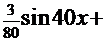 +
+ 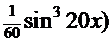 .
.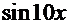 =
= 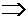
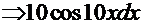 =
= 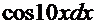 =
= 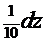 .
. 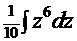 =
= 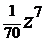 . После обратной замены
. После обратной замены 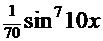 .
.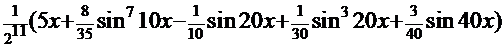 +С.
+С.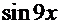 и её дифференциал:
и её дифференциал: 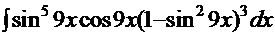 . Воспользовавшись формулой
. Воспользовавшись формулой 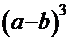 =
= 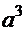
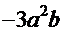 +
+ 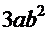
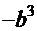 и введя замену
и введя замену 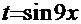
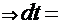
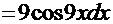
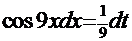 , получаем интеграл
, получаем интеграл 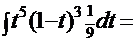 =
= 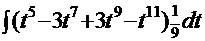 . Этот интеграл легко решается:
. Этот интеграл легко решается: 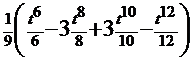 +С=
+С= 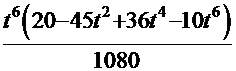 +С.
+С.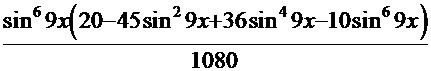 +С.
+С.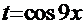 или
или 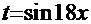 и др.
и др.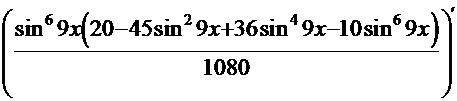 =
=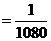
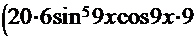 ─
─ 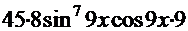 +
+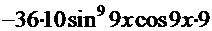
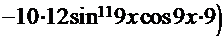 =
=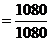
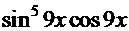
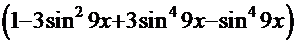 =
=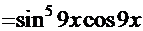
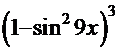 =
= 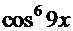 =
=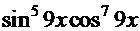 ─ правильность решения подтверждена.
─ правильность решения подтверждена.


