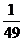Пример решения простейшего интеграла.
Пример 0

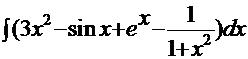 .
.
Рецепт.
Используя свойство 4 (см. стр. 6), преобразуем «интеграл от суммы функций» в «сумму интегралов от функций»: 
 +
+ 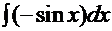 +
+  +
+  .
.
Нетрудно заметить, что подынтегральная функция первого интеграла 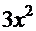
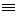
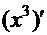 . Аналогичная картина и в остальных интегралах:
. Аналогичная картина и в остальных интегралах: 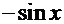 =
= 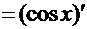 ,
, 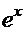 =
=  ,
, 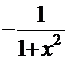 =
= 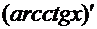 .
.
Если вспомнить формулу дифференциала, то получим 
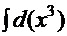 +
+ 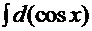 +
+ 
 , т.е. мы имеем дело с элементарными «табличными» интегралами.
, т.е. мы имеем дело с элементарными «табличными» интегралами.
Тогда конечный итог: 
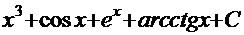 .
.
На будущее:
тактика вычисления любых неопределённых интегралов должна сводиться к такому преобразованию подынтегральной функции, чтобы её структура была похожа на структуру только что приведённого примера.
Поскольку многообразие подынтегральных функций практически неограниченно, то ниже предлагаются несколько «стандартных» приёмов преобразования подынтегральных функций, чтобы Вам не приходилось заново «изобретать велосипед».
Наиболее популярные методы решения неопределённых интегралов
Замена переменной интегрирования.
Пример 1. 
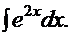
Рецепт. Вводим замену 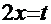 . Отсюда:
. Отсюда: 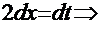 (вспомним формулу дифференциала)
(вспомним формулу дифференциала) 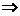
 . Тогда
. Тогда 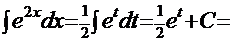 (обратная подстановка)
(обратная подстановка) 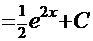 .
.
Пример 2. 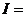
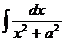
В таблице элементарных интегралов имеется формула аналогичного интеграла:
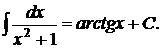 Однако чаще же всего встречается более общий вариант этого интеграла:
Однако чаще же всего встречается более общий вариант этого интеграла: 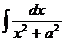 , где
, где 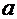 ─ некая числовая константа.
─ некая числовая константа.
Рецепт. Выносим  из знаменателя (а, значит, и из-под знака интеграла):
из знаменателя (а, значит, и из-под знака интеграла):
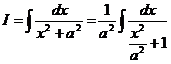 и делаем замену:
и делаем замену: 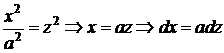 . Тогда
. Тогда 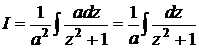 . А это уже знакомый табличный интеграл. Отсюда
. А это уже знакомый табличный интеграл. Отсюда 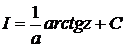 . Проводим обратную подстановку
. Проводим обратную подстановку 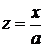 и получаем в результате
и получаем в результате 
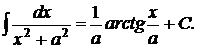
Полученным интегралом рекомендуем пополнить уже имеющуюся таблицу.
Приведение к «табличному виду».
Пример 3. 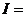
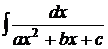 Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Рецепт. Преобразуем трёхчлен знаменателя к виду, похожему на квадратный двучлен табличного интеграла, рассмотренного в Примере 2. Последовательность действий должна быть следующей:
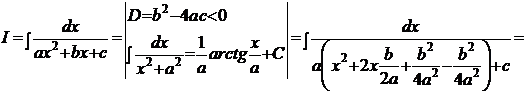
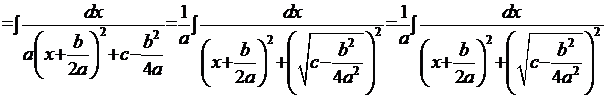
Очевидно, что этот интеграл по своей структуре полностью соответствует интегралу Примера 2: переменной 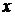 этого интеграла соответствует переменная
этого интеграла соответствует переменная  , а множителю
, а множителю  соответствует радикал:
соответствует радикал: 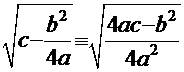
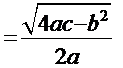 . Далее
. Далее 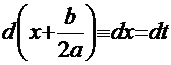 . Отсюда решение интеграла:
. Отсюда решение интеграла: 

N.B.! Помните, что нельзя полностью доверять авторам любого учебного пособия (кто из нас не без греха?), в том числе и авторам данного пособия. Поэтому убедительная просьба: для проверки правильности взятия интеграла старайтесь почаще применять первое свойство интегралов!
Замена функции.
Для этого приёма характерно многообразие вариантов замены какой-либо функции, входящей в подынтегральную функцию. Удача чаще всего приходит только в случае перебора нескольких вариантов.
Пример 4.  .
.
Рецепт. Здесь безальтернативный вариант замены:  . Это – табличный интеграл:
. Это – табличный интеграл: 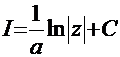 . Обратная подстановка
. Обратная подстановка  приводит к конечному результату:
приводит к конечному результату:  .
.
Пример 5. 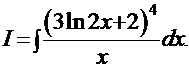
Рецепт. Опытный взгляд обнаружит интересную дробь  ─ дифференциал функции
─ дифференциал функции 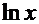 , а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену:
, а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену: 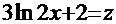 . Тогда
. Тогда 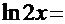


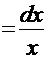
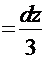 . В результате этой подстановки имеем табличный интеграл:
. В результате этой подстановки имеем табличный интеграл: 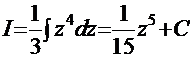 . Обратная подстановка приводит к конечному результату
. Обратная подстановка приводит к конечному результату 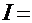
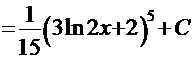 .
.
К этой же группе интегралов, требующих замены функции, относятся такие, в составе которых имеются радикалы 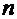 ой степени
ой степени 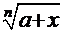 , т.е. компоненты типа
, т.е. компоненты типа 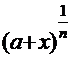 . Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
. Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
Пример 6. 
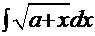 .
.
Рецепт. Здесь 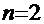 . Очевидна замена
. Очевидна замена 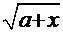 =
= 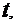 тогда
тогда 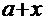 =
= 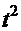
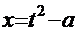
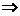
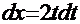 . Тогда интеграл легко приводится к
. Тогда интеграл легко приводится к 
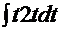 = =
= = 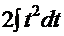
 +С.
+С.
Обратная подстановка даёт конечный результат: 
 =
= 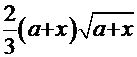 +С.
+С.
Интегрирование «по частям»
Идея этого метода основана на формуле производной произведения двух функций: 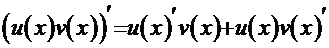 [1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций:
[1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций: 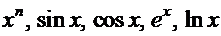 и их вариаций.
и их вариаций.
Итак, если подынтегральную функцию 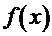 можно представить в виде произведения
можно представить в виде произведения 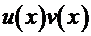 , то сочетание
, то сочетание 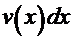 или
или  можно принять за дифференциал
можно принять за дифференциал 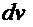 или
или 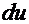 . Тогда решение интеграла получается по формуле:
. Тогда решение интеграла получается по формуле: 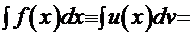

Выбор функций-сомножителей определяется опытом самого решающего. Попытаемся показать это на конкретном примере.
Пример 7.  .
.
Рецепт. Альтернатива выбора функций-сомножителей здесь небогатая: либо 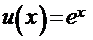 и
и 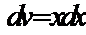 , либо
, либо 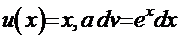 . Попробуем пойти первым путём
. Попробуем пойти первым путём
Вариант 1. 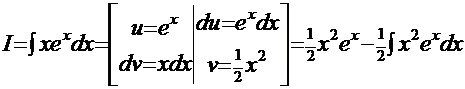 . Повторно применяем этот же метод:
. Повторно применяем этот же метод:  и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции
и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции 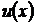 .
.
Не следует думать, что есть люди, которые ни разу не совершали подобную ошибку, просто из этого надо сделать позитивный вывод: «на ошибках учатся».
А теперь пойдём альтернативным путём:
Вариант 2: 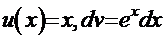 . Тогда
. Тогда 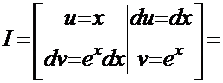
 .
.
Интересной особенностью данного метода является решение «рекурсивных интегралов». Рассмотрим один из вариантов таких интегралов.
Пример 8. 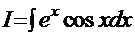 .
.
Рецепт. Применим метод «по частям»: 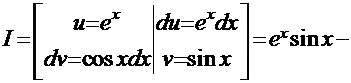
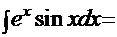


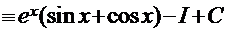
Сопоставив начало и конец этой цепочки, получаем решение 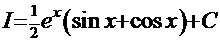 .
.
5. Рациональные дроби
Известно [1], что дробь может называться «рациональной», если её числитель и знаменатель ─ целые числа. С этой точки зрения излагаемый дальше метод относится к интегралам вида: 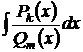 , где
, где  , а
, а 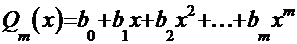 ─ полиномы порядка
─ полиномы порядка 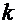 и
и  , соответственно.
, соответственно.
С точки зрения соотношения порядков полиномов возможны два варианта:
a)  . В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов:
. В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов: 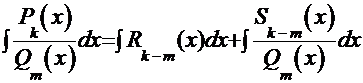 , где
, где 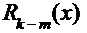
и 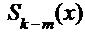 ─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
b) 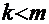 . Здесь сразу берётся интеграл указанным выше методом.
. Здесь сразу берётся интеграл указанным выше методом.
Тригонометрические функции.
Специфика взятия интегралов, в которых подынтегральная функция включает в себя тригонометрические функции, заключается в большом разнообразии возможных приёмов интегрирования. Это обусловлено таким же большим разнообразием тригонометрических формул, с помощью которых можно представить одну и ту же тригонометрическую функцию.
Ниже мы рассмотрим наиболее часто используемые приёмы для решения таких интегралов, а пользователь может по своему усмотрению применять тот или другой приём для решения интегралов из своего задания.
6.1. Интегралы типа 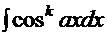 ,
, 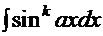 .
.
а) вариант 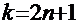 (нечётная степень):
(нечётная степень): 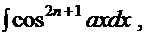
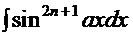
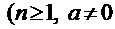
 . Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл
. Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл 
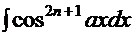 . Перепишем его в другой форме:
. Перепишем его в другой форме: 
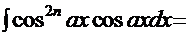
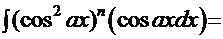
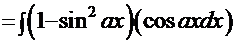 . Очевидна замена:
. Очевидна замена: 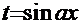
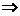


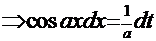 . Тогда
. Тогда 
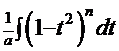 . После раскрытия скобок для соответствующего значения
. После раскрытия скобок для соответствующего значения 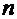 искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл
искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл  с той лишь разницей, что заменяется
с той лишь разницей, что заменяется  .
.
Пример 12. 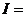

Рецепт. Вводим замену 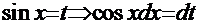 .
. 

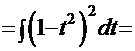
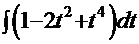 =
=  . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 
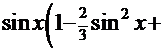
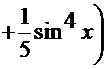

б) вариант  (чётная степень):
(чётная степень):  .
.
Для данных интегралов используется другая схема: с помощью известных в тригонометрии формул 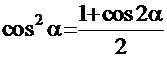 и
и 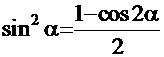 вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от
вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от 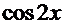 в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
Пример 13. 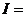

Рецепт. С помощью приведённых выше формул преобразуем интеграл: 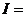
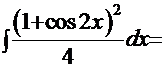
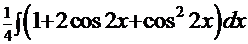


 .
.
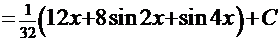
6.2. Интегралы типа 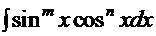
Интегралы этого типа несколько сложнее интегралов из предыдущего раздела. Возможны, естественно, три варианта:
а) один из показателей степени нечётный, другой─ чётный, т.е.
либо 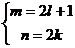 , либо
, либо  , где
, где  и
и 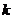 ─ целые числа.
─ целые числа.
Рассмотрим, например, первый вариант и преобразуем интеграл к виду: 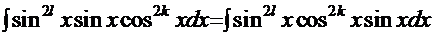 . Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену
. Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену 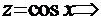
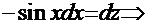
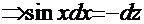 и воспользоваться основным тригонометрическим тождеством
и воспользоваться основным тригонометрическим тождеством 
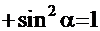 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 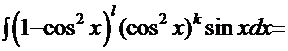
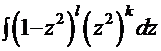 .
.
Раскрывая скобки для соответствующих степеней, получаем сумму интегралов от степенной функции.
Пример 14. 

Рецепт. Вводим замену  и получаем
и получаем 

 . Обратная подстановка приводит к окончательному ответу
. Обратная подстановка приводит к окончательному ответу 
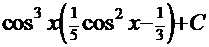 .
.
б ) оба показателя чётные:  . Тогда с помощью формул
. Тогда с помощью формул 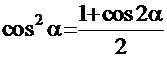 и
и 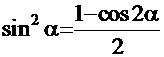 интеграл преобразуется:
интеграл преобразуется: 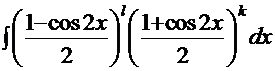 . Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
. Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
Пример 15. 

Рецепт 1. Используя преобразования, описанные выше, получим интеграл 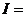
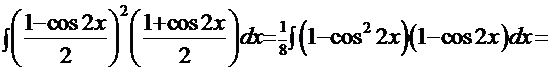
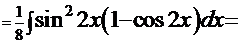
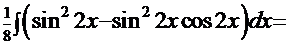

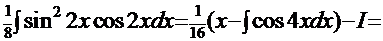
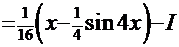 . Здесь
. Здесь  . Используем замену:
. Используем замену: 

 . Тогда
. Тогда 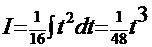 . Сделаем обратную подстановку и получим желанное решение:
. Сделаем обратную подстановку и получим желанное решение: 
 .
.
Рецепт 2. Можно использовать и другой путь:  . Тогда подынтегральная функция получит следующий вид:
. Тогда подынтегральная функция получит следующий вид:  =
= 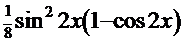 , а сам интеграл:
, а сам интеграл: 
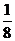
 =
= 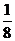
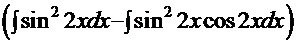 =
= 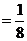
 -
- 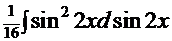 =
= 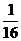
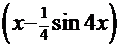 -
- 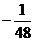
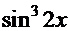 =
=  .
.
Совпадение конечного результата по обоим рецептам свидельствует о правильности альтернатив решения одного и того же интеграла.
в) и, наконец, третий вариант – оба показателя нечётные: 
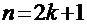 . Преобразуем интеграл к виду:
. Преобразуем интеграл к виду: 


 . Снова воспользуемся формулами удвоенного аргумента функции косинуса:
. Снова воспользуемся формулами удвоенного аргумента функции косинуса: 
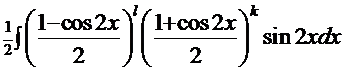 . Очевидно, что напрашивается замена:
. Очевидно, что напрашивается замена: 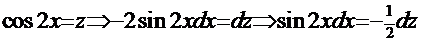 : тогда интеграл принимает вид:
: тогда интеграл принимает вид: 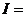
 . Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
. Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
Пример 16 
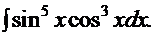
Рецепт. Используем преобразования, описанные выше, и получаем интеграл

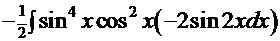 . Замена:
. Замена: 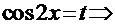
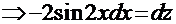 преобразует интеграл
преобразует интеграл 
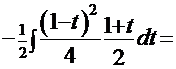
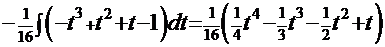 . После обратной подстановки имеем решение
. После обратной подстановки имеем решение 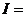
 .
.
Каждый из этих трёх вариантов решения требует своего подхода. Но есть ещё один приём:
г) «универсальная тригонометрическая подстановка»  , для которой находим дифференциал
, для которой находим дифференциал 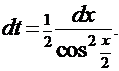 Отсюда
Отсюда 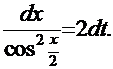 Применим этот приём к уже знакомому интегралу из Примера 11
Применим этот приём к уже знакомому интегралу из Примера 11 
 . Подставив введённые выше выражения для
. Подставив введённые выше выражения для 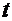 и
и 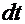 , получаем интеграл:
, получаем интеграл:  Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»:
Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»: 

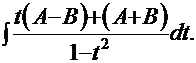 Решаем простую систему линейных уравнений:
Решаем простую систему линейных уравнений:  . Результат:
. Результат: 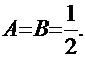 Продолжим решение интеграла:
Продолжим решение интеграла:  =
= 
 Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем
Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем  Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
N.B.! Имеются данные [1], что использование «универсальной подстановки» может привести к громоздким преобразованиям, что несколько снижает его ценность.
6.3. Интегралы типа 
Поверхностный взгляд на подынтегральные функции данной группы вызывает очевидные ассоциации с формулами  и
и  . Вспомним, что:
. Вспомним, что:

Рассмотрим для примера решение интеграла 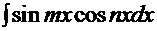 . Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет
. Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет 
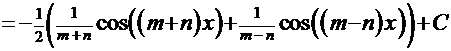 .
.
Аналогично решаются и остальные интегралы.
Пример 17. 
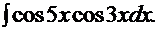
Рецепт. Применив одну из ранее приведённых формул, получаем решение:

 .
.
6.4. Интегралы типа 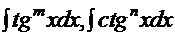
Такого рода интегралы сводятся к табличным интегралам простой подстановкой: 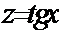 для первого интеграла и
для первого интеграла и 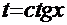 - для второго.
- для второго.
Пример 18. 
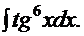
Рецепт. Используем замену 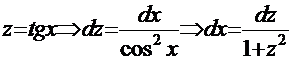 и получаем решение
и получаем решение 
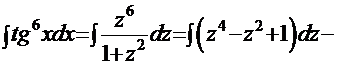
 =
= 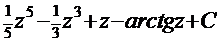 . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 
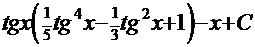 .
.
Пример 19. 
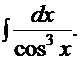
Рецепт. Ранее был рассмотрен интеграл  , поэтому данный интеграл решаем рассмотренным ранее методом «по частям»:
, поэтому данный интеграл решаем рассмотренным ранее методом «по частям»: 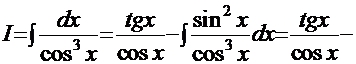

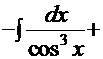
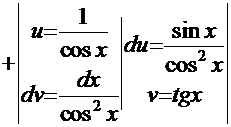
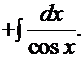 Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл
Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл 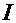
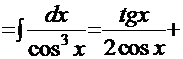

6.5. Интегралы типа 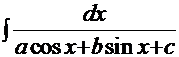 .
.
К таким интегралам наиболее эффективно (а зачастую – единственным образом) применение описанной выше «универсальной подстановки»: 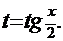
Вспомним, что  ,
, 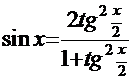 , и (см. стр. 16)
, и (см. стр. 16) 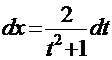 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 
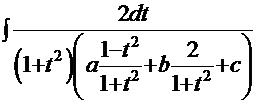 =
=  = =
= = 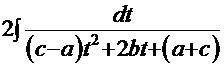 .
.
В зависимости от конкретного сочетания значений коэффициентов  получаем два основных исхода (с вариациями):
получаем два основных исхода (с вариациями):
1. 
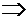 см. Пример 4.
см. Пример 4.
2. 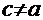 . Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя
. Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя 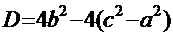 =
= 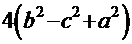 на два варианта:
на два варианта:
2а: 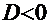 ─ см. Пример 3;
─ см. Пример 3;
2б: 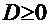 ─ см. Пример 9.
─ см. Пример 9.
Рассмотрим конкретный пример:
Пример 20. 
 .
.
Рецепт. Здесь  ,
, 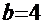 ,
,  ,
, 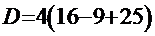 =
= 
 .
.
Согласно вышеприведённой формуле с использованием универсальной подстановки  данный интеграл получает вид
данный интеграл получает вид 
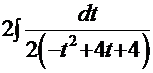 = =
= =  . Значение дискриминанта
. Значение дискриминанта 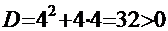 . Тогда корни трёхчлена знаменателя вычисляем по формуле
. Тогда корни трёхчлена знаменателя вычисляем по формуле 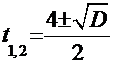 =
=  . В соответствии с методом «неопределённых коэффициентов»
. В соответствии с методом «неопределённых коэффициентов» 
 =
=
= 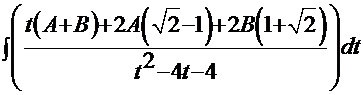 . Отсюда имеем систему двух линейных уравнений для коэффициентов
. Отсюда имеем систему двух линейных уравнений для коэффициентов  и
и 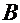 :
:  . Тогда
. Тогда 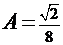 и
и 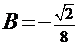 , а
, а 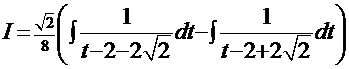 =
= 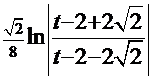 . Обратная подстановка
. Обратная подстановка  даёт конечный ответ
даёт конечный ответ 
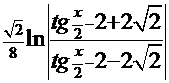 +С.
+С.
Примечания
1. Все 25 заданий приводятся в ПРИЛОЖЕНИИ 1.
2. Выполнение каждой задачи данного демонстрационного варианта должен сопровождаться проверкой решения (см. образец).
1. 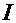 =
= 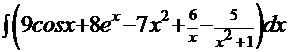 . Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем:
. Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем: 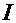 =
= 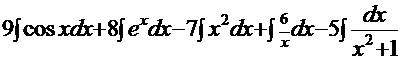 , а это – табличные интегралы, поэтому решение:
, а это – табличные интегралы, поэтому решение: 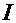 =
= 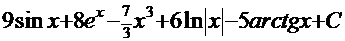 .
.
ПРОВЕРКА 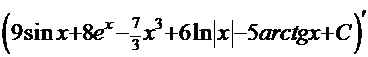 =
= 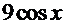 +
+ 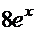 ─
─ 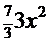 +
+ 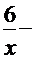
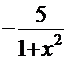 =
= 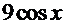 +
+ 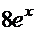
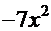 +
+ 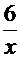
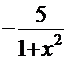 . Получено полное совпадение с подынтегральной функцией решаемого интеграла, значит, решение - верное.
. Получено полное совпадение с подынтегральной функцией решаемого интеграла, значит, решение - верное.
Ответ 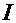 =
=  .
.
2.  =
= 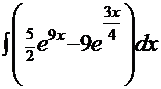 =
= 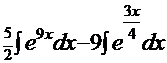 =
= 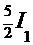
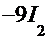 . Для решения обоих интегралов используем приём «замены переменных»:
. Для решения обоих интегралов используем приём «замены переменных»: 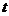 =
= 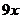 для интеграла
для интеграла 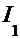 и
и 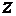 =
= 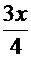 - для интеграла
- для интеграла 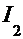 . Тогда
. Тогда 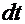 =
= 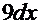
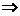
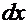 =
= 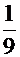
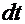 . Получаем
. Получаем 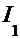 =
= 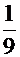
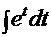 (табличный интеграл)=
(табличный интеграл)= 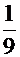
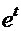 . С помощью обратной подстановки получаем
. С помощью обратной подстановки получаем 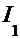 =
= 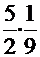
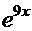 =
= 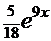 .
.
Аналогичные преобразования для интеграла 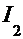 :
: 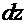 =
= 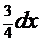
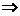
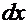 =
= 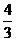
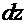 приводят к результату
приводят к результату 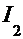 =
= 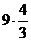
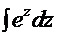 =
= 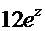 =
= 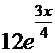 . Таким образом, общее решение
. Таким образом, общее решение  =
= 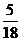
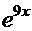
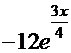 +С.
+С.
ПРОВЕРКА (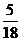
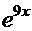
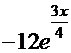 +С)
+С)  =
= 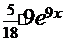
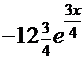 =
= 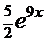
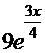 ─ очевидное совпадение.
─ очевидное совпадение.
Ответ: 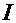 =
= 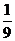
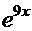 +
+ 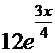 +С.
+С.
3. 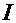 =
= 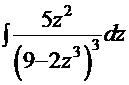 . Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»:
. Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»:  =
= 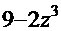 . Тогда дифференциал
. Тогда дифференциал 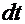 =
= 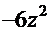
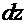
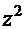
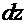 =
= 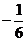
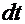 и интеграл принимает вид
и интеграл принимает вид 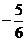
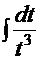 , т.е. снова табличный интеграл
, т.е. снова табличный интеграл 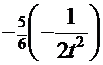 =
= 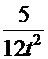 . После обратной замены получаем
. После обратной замены получаем 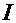 =
= 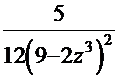 .
.
ПРОВЕРКА: 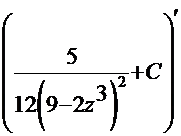 =
= 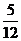
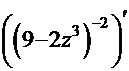 =
= 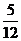
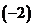
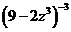
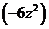 =
=
= 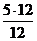
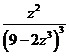 =
= 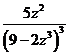 - снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
- снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
Ответ 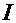 =
= 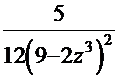 +С.
+С.
4. 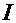 =
= 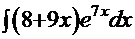 . Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»:
. Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»: 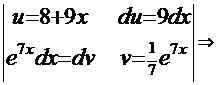
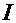 =
= 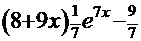
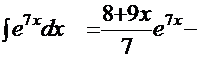
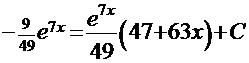 .
.
ПРОВЕРКА 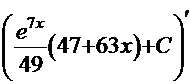 =
= 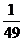

|
|
|




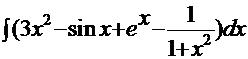 .
. +
+ 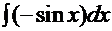 +
+  +
+  .
.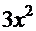
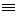
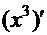 . Аналогичная картина и в остальных интегралах:
. Аналогичная картина и в остальных интегралах: 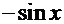 =
= 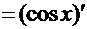 ,
, 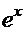 =
=  ,
, 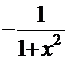 =
= 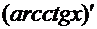 .
.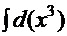 +
+ 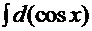 +
+ 
 , т.е. мы имеем дело с элементарными «табличными» интегралами.
, т.е. мы имеем дело с элементарными «табличными» интегралами.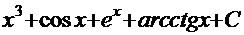 .
.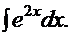
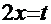 . Отсюда:
. Отсюда: 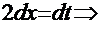 (вспомним формулу дифференциала)
(вспомним формулу дифференциала) 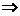
 . Тогда
. Тогда 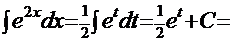 (обратная подстановка)
(обратная подстановка) 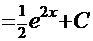 .
.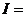
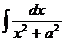
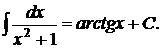 Однако чаще же всего встречается более общий вариант этого интеграла:
Однако чаще же всего встречается более общий вариант этого интеграла: 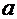 ─ некая числовая константа.
─ некая числовая константа. из знаменателя (а, значит, и из-под знака интеграла):
из знаменателя (а, значит, и из-под знака интеграла):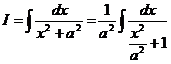 и делаем замену:
и делаем замену: 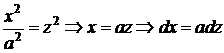 . Тогда
. Тогда 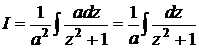 . А это уже знакомый табличный интеграл. Отсюда
. А это уже знакомый табличный интеграл. Отсюда 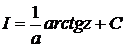 . Проводим обратную подстановку
. Проводим обратную подстановку 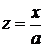 и получаем в результате
и получаем в результате 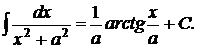
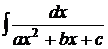 Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).
Здесь рассматривается вариант, при котором дискриминант знаменателя существенно отрицательный (остальные варианты исследуются ниже).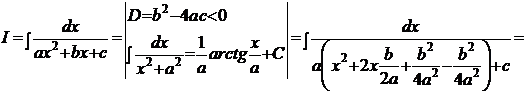
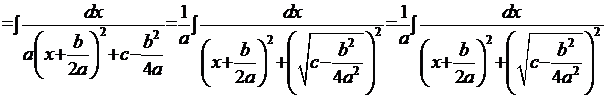
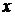 этого интеграла соответствует переменная
этого интеграла соответствует переменная  , а множителю
, а множителю  соответствует радикал:
соответствует радикал: 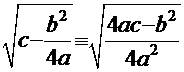
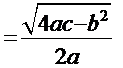 . Далее
. Далее 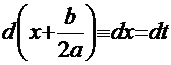 . Отсюда решение интеграла:
. Отсюда решение интеграла: 
 .
. . Это – табличный интеграл:
. Это – табличный интеграл: 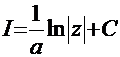 . Обратная подстановка
. Обратная подстановка  приводит к конечному результату:
приводит к конечному результату:  .
.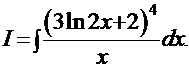
 ─ дифференциал функции
─ дифференциал функции 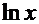 , а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену:
, а в числителе дроби встречается именно такая функция. Отсюда должна появиться естественная мысль сделать замену: 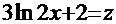 . Тогда
. Тогда 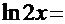


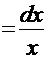
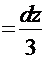 . В результате этой подстановки имеем табличный интеграл:
. В результате этой подстановки имеем табличный интеграл: 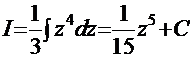 . Обратная подстановка приводит к конечному результату
. Обратная подстановка приводит к конечному результату 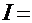
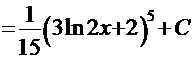 .
.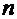 ой степени
ой степени 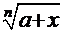 , т.е. компоненты типа
, т.е. компоненты типа 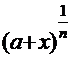 . Очевидно, такой радикал надо заменить какой-либо переменной того же типа.
. Очевидно, такой радикал надо заменить какой-либо переменной того же типа.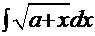 .
.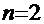 . Очевидна замена
. Очевидна замена 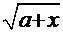 =
= 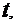 тогда
тогда 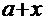 =
= 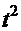
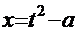
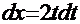 . Тогда интеграл легко приводится к
. Тогда интеграл легко приводится к 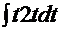 = =
= = 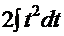
 +С.
+С. =
= 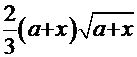 +С.
+С.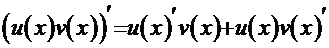 [1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций:
[1] и применяется чаще всего тогда, когда подынтегральная функция может быть представлена в виде произведения пары хотя бы одной из следующих функций: 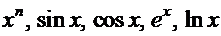 и их вариаций.
и их вариаций.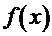 можно представить в виде произведения
можно представить в виде произведения 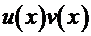 , то сочетание
, то сочетание 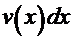 или
или  можно принять за дифференциал
можно принять за дифференциал 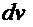 или
или 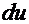 . Тогда решение интеграла получается по формуле:
. Тогда решение интеграла получается по формуле: 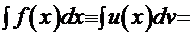

 .
.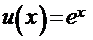 и
и 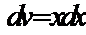 , либо
, либо 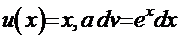 . Попробуем пойти первым путём
. Попробуем пойти первым путём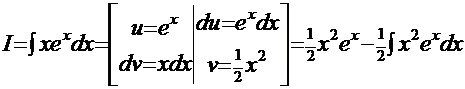 . Повторно применяем этот же метод:
. Повторно применяем этот же метод:  и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции
и т.д. Очевидно, что этот путь - тупиковый: с каждым новым шагом показатель степени при аргументе растёт и не видно конца этим манипуляциям. Очевидна и причина такого тупика - неудачный первоначальный выбор функции 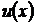 .
.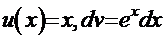 . Тогда
. Тогда 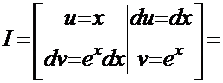
 .
.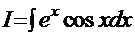 .
.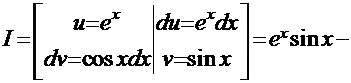
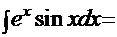


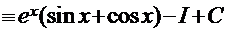
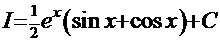 .
.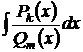 , где
, где  , а
, а 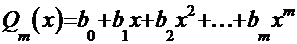 ─ полиномы порядка
─ полиномы порядка 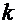 и
и  , соответственно.
, соответственно. . В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов:
. В этом случае полином числителя «столбиком» делят на полином знаменателя, выделяя тем самым «целую» часть подынтегральной дроби и её «остаток». Тогда исходный интеграл можно представить в виде суммы двух интегралов: 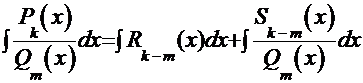 , где
, где 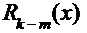
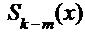 ─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;
─ полиномы соответствующего порядка того же типа, что и исходные полиномы. Первый интеграл – сумма табличных интегралов. Ко второму интегралу применяют обычно метод «неопределённых коэффициентов», суть которого излагается дальше;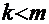 . Здесь сразу берётся интеграл указанным выше методом.
. Здесь сразу берётся интеграл указанным выше методом.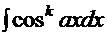 ,
, 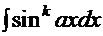 .
.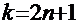 (нечётная степень):
(нечётная степень): 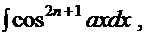
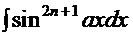
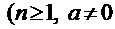
 . Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл
. Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл 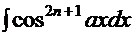 . Перепишем его в другой форме:
. Перепишем его в другой форме: 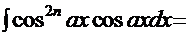
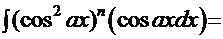
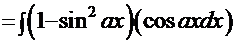 . Очевидна замена:
. Очевидна замена: 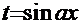


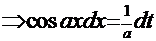 . Тогда
. Тогда 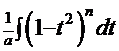 . После раскрытия скобок для соответствующего значения
. После раскрытия скобок для соответствующего значения  с той лишь разницей, что заменяется
с той лишь разницей, что заменяется  .
.
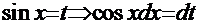 .
. 
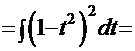
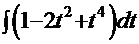 =
=  . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 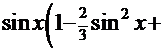
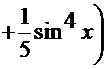

 (чётная степень):
(чётная степень):  .
.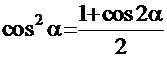 и
и 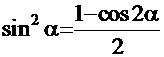 вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от
вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от 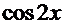 в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
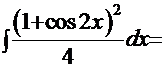
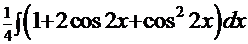


 .
.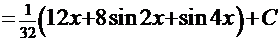
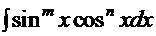
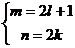 , либо
, либо  , где
, где  и
и 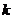 ─ целые числа.
─ целые числа.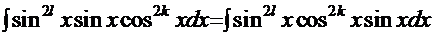 . Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену
. Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену 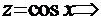
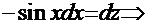
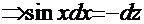 и воспользоваться основным тригонометрическим тождеством
и воспользоваться основным тригонометрическим тождеством 
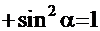 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 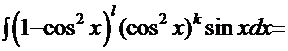
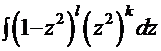 .
.
 и получаем
и получаем 
 . Обратная подстановка приводит к окончательному ответу
. Обратная подстановка приводит к окончательному ответу 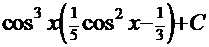 .
. . Тогда с помощью формул
. Тогда с помощью формул 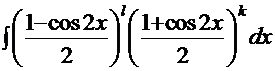 . Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
. Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
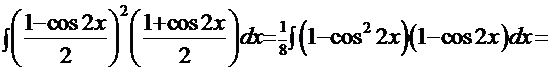
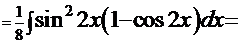
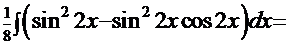

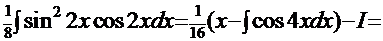
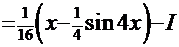 . Здесь
. Здесь  . Используем замену:
. Используем замену: 

 . Тогда
. Тогда 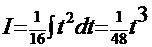 . Сделаем обратную подстановку и получим желанное решение:
. Сделаем обратную подстановку и получим желанное решение:  .
. . Тогда подынтегральная функция получит следующий вид:
. Тогда подынтегральная функция получит следующий вид:  =
= 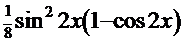 , а сам интеграл:
, а сам интеграл: 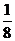
 =
= 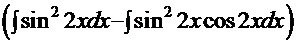 =
= 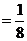
 -
- 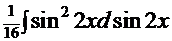 =
= 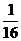
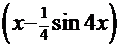 -
- 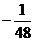
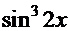 =
= 
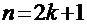 . Преобразуем интеграл к виду:
. Преобразуем интеграл к виду: 

 . Снова воспользуемся формулами удвоенного аргумента функции косинуса:
. Снова воспользуемся формулами удвоенного аргумента функции косинуса: 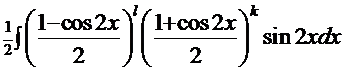 . Очевидно, что напрашивается замена:
. Очевидно, что напрашивается замена: 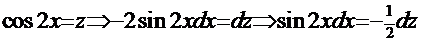 : тогда интеграл принимает вид:
: тогда интеграл принимает вид:  . Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
. Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.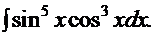
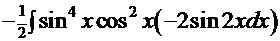 . Замена:
. Замена: 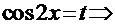
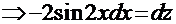 преобразует интеграл
преобразует интеграл 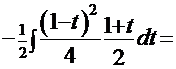
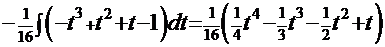 . После обратной подстановки имеем решение
. После обратной подстановки имеем решение  .
. , для которой находим дифференциал
, для которой находим дифференциал 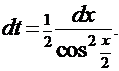 Отсюда
Отсюда 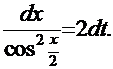 Применим этот приём к уже знакомому интегралу из Примера 11
Применим этот приём к уже знакомому интегралу из Примера 11 
 . Подставив введённые выше выражения для
. Подставив введённые выше выражения для 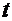 и
и 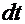 , получаем интеграл:
, получаем интеграл:  Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»:
Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»: 

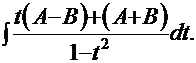 Решаем простую систему линейных уравнений:
Решаем простую систему линейных уравнений:  . Результат:
. Результат: 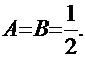 Продолжим решение интеграла:
Продолжим решение интеграла:  =
=  Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем
Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем  Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
 и
и  . Вспомним, что:
. Вспомним, что:
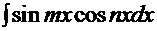 . Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет
. Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет 
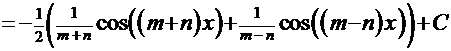 .
.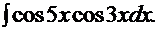
 .
.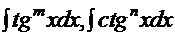
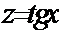 для первого интеграла и
для первого интеграла и 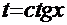 - для второго.
- для второго.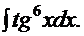
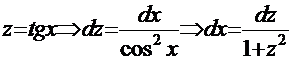 и получаем решение
и получаем решение 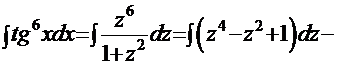
 =
= 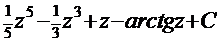 . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 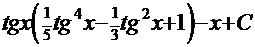 .
.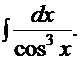
 , поэтому данный интеграл решаем рассмотренным ранее методом «по частям»:
, поэтому данный интеграл решаем рассмотренным ранее методом «по частям»: 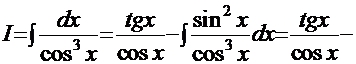

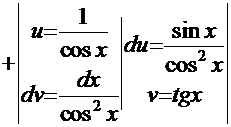
 Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл
Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл 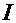
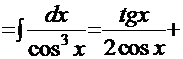

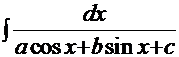 .
.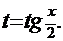
 ,
, 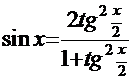 , и (см. стр. 16)
, и (см. стр. 16) 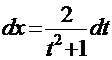 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 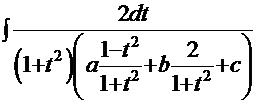 =
=  = =
= = 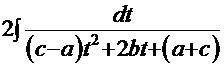 .
. получаем два основных исхода (с вариациями):
получаем два основных исхода (с вариациями):
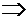 см. Пример 4.
см. Пример 4.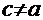 . Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя
. Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя 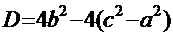 =
= 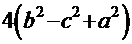 на два варианта:
на два варианта: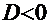 ─ см. Пример 3;
─ см. Пример 3;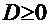 ─ см. Пример 9.
─ см. Пример 9. .
. ,
, 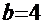 ,
,  ,
, 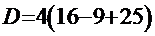 =
= 
 .
. данный интеграл получает вид
данный интеграл получает вид 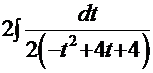 = =
= =  . Значение дискриминанта
. Значение дискриминанта 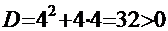 . Тогда корни трёхчлена знаменателя вычисляем по формуле
. Тогда корни трёхчлена знаменателя вычисляем по формуле 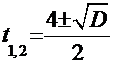 =
=  . В соответствии с методом «неопределённых коэффициентов»
. В соответствии с методом «неопределённых коэффициентов» 
 =
=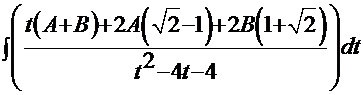 . Отсюда имеем систему двух линейных уравнений для коэффициентов
. Отсюда имеем систему двух линейных уравнений для коэффициентов  и
и 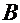 :
:  . Тогда
. Тогда 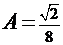 и
и 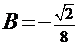 , а
, а 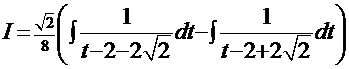 =
= 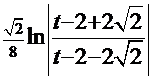 . Обратная подстановка
. Обратная подстановка 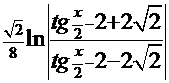 +С.
+С.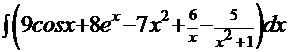 . Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем:
. Согласно свойствам 3 и 4 («константу желательно выносить за знак интеграла» и «интеграл суммы функций равен сумме интегралов от каждой функции») получаем: 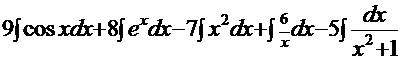 , а это – табличные интегралы, поэтому решение:
, а это – табличные интегралы, поэтому решение: 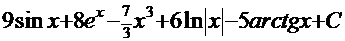 .
.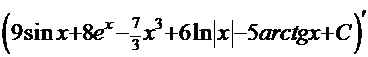 =
= 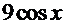 +
+ 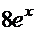 ─
─ 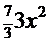 +
+ 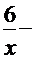
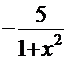 =
= 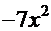 +
+ 
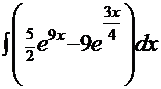 =
= 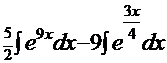 =
= 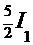
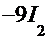 . Для решения обоих интегралов используем приём «замены переменных»:
. Для решения обоих интегралов используем приём «замены переменных»: 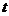 =
= 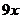 для интеграла
для интеграла 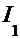 и
и 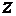 =
= 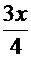 - для интеграла
- для интеграла 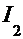 . Тогда
. Тогда 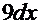
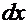 =
= 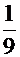
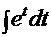 (табличный интеграл)=
(табличный интеграл)= 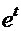 . С помощью обратной подстановки получаем
. С помощью обратной подстановки получаем 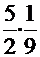
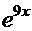 =
= 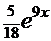 .
.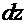 =
= 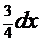
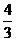
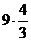
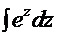 =
= 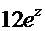 =
= 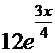 . Таким образом, общее решение
. Таким образом, общее решение 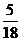
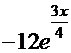 +С.
+С. =
= 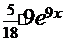
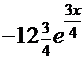 =
= 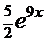
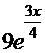 ─ очевидное совпадение.
─ очевидное совпадение.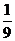
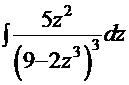 . Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»:
. Если присмотреться к числителю дроби, то без труда можно увидеть элементы производной выражения в знаменателе. Поэтому логично было бы использовать приём «замена функции»: 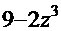 . Тогда дифференциал
. Тогда дифференциал 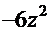
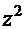
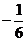
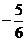
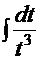 , т.е. снова табличный интеграл
, т.е. снова табличный интеграл 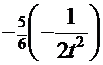 =
= 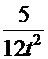 . После обратной замены получаем
. После обратной замены получаем 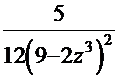 .
.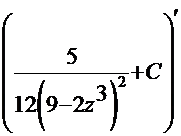 =
= 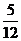
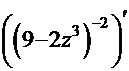 =
= 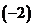
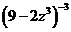
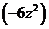 =
=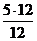
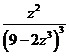 =
= 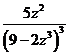 - снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.
- снова имеем полное совпадение выражения производной результата и подынтегральной функции решённого интеграла.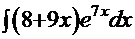 . Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»:
. Подынтегральная функция данной задачи при сравнении с той же функцией Примера 7 наводит на мысль использовать метод «по частям»: 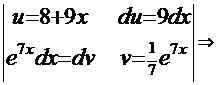
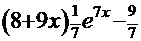
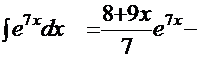
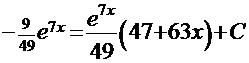 .
.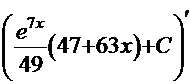 =
=