Тригонометрические функции.
Специфика взятия интегралов, в которых подынтегральная функция включает в себя тригонометрические функции, заключается в большом разнообразии возможных приёмов интегрирования. Это обусловлено таким же большим разнообразием тригонометрических формул, с помощью которых можно представить одну и ту же тригонометрическую функцию.
Ниже мы рассмотрим наиболее часто используемые приёмы для решения таких интегралов, а пользователь может по своему усмотрению применять тот или другой приём для решения интегралов из своего задания.
6.1. Интегралы типа 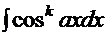 ,
, 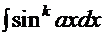 .
.
а) вариант 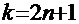 (нечётная степень):
(нечётная степень): 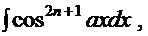
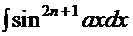
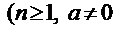
 . Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл
. Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл 
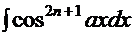 . Перепишем его в другой форме:
. Перепишем его в другой форме: 
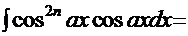
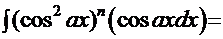
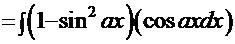 . Очевидна замена:
. Очевидна замена: 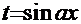



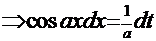 . Тогда
. Тогда 
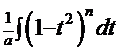 . После раскрытия скобок для соответствующего значения
. После раскрытия скобок для соответствующего значения 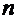 искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл
искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл  с той лишь разницей, что заменяется
с той лишь разницей, что заменяется  .
.
Пример 12. 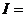

Рецепт. Вводим замену 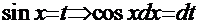 .
. 

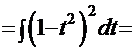
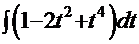 =
=  . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 
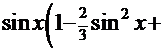
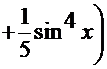

б) вариант  (чётная степень):
(чётная степень):  .
.
Для данных интегралов используется другая схема: с помощью известных в тригонометрии формул 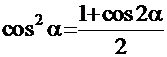 и
и 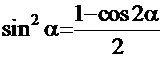 вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от
вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от 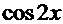 в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
Пример 13. 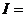

Рецепт. С помощью приведённых выше формул преобразуем интеграл: 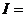
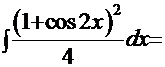
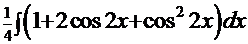


 .
.
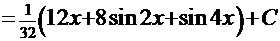
6.2. Интегралы типа 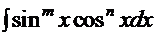
Интегралы этого типа несколько сложнее интегралов из предыдущего раздела. Возможны, естественно, три варианта:
а) один из показателей степени нечётный, другой─ чётный, т.е.
либо 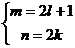 , либо
, либо  , где
, где  и
и 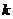 ─ целые числа.
─ целые числа.
Рассмотрим, например, первый вариант и преобразуем интеграл к виду: 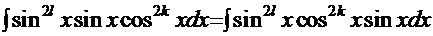 . Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену
. Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену 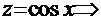
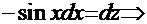
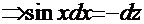 и воспользоваться основным тригонометрическим тождеством
и воспользоваться основным тригонометрическим тождеством 
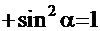 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 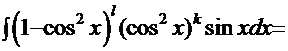
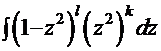 .
.
Раскрывая скобки для соответствующих степеней, получаем сумму интегралов от степенной функции.
Пример 14. 

Рецепт. Вводим замену  и получаем
и получаем 

 . Обратная подстановка приводит к окончательному ответу
. Обратная подстановка приводит к окончательному ответу 
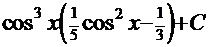 .
.
б ) оба показателя чётные:  . Тогда с помощью формул
. Тогда с помощью формул 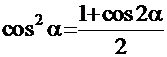 и
и 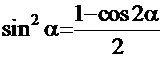 интеграл преобразуется:
интеграл преобразуется: 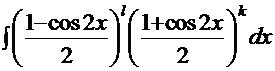 . Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
. Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
Пример 15. 

Рецепт 1. Используя преобразования, описанные выше, получим интеграл 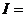
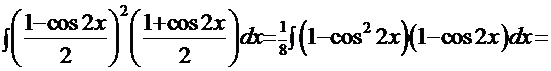
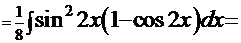
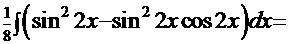

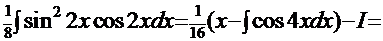
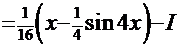 . Здесь
. Здесь  . Используем замену:
. Используем замену: 

 . Тогда
. Тогда 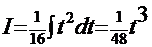 . Сделаем обратную подстановку и получим желанное решение:
. Сделаем обратную подстановку и получим желанное решение: 
 .
.
Рецепт 2. Можно использовать и другой путь:  . Тогда подынтегральная функция получит следующий вид:
. Тогда подынтегральная функция получит следующий вид:  =
= 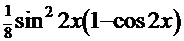 , а сам интеграл:
, а сам интеграл: 
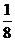
 =
= 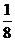
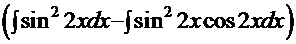 =
= 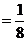
 -
- 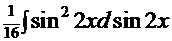 =
= 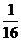
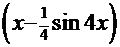 -
- 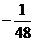
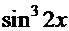 =
=  .
.
Совпадение конечного результата по обоим рецептам свидельствует о правильности альтернатив решения одного и того же интеграла.
в) и, наконец, третий вариант – оба показателя нечётные: 
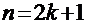 . Преобразуем интеграл к виду:
. Преобразуем интеграл к виду: 


 . Снова воспользуемся формулами удвоенного аргумента функции косинуса:
. Снова воспользуемся формулами удвоенного аргумента функции косинуса: 
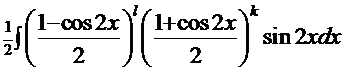 . Очевидно, что напрашивается замена:
. Очевидно, что напрашивается замена: 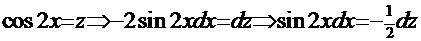 : тогда интеграл принимает вид:
: тогда интеграл принимает вид: 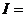
 . Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
. Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
Пример 16 
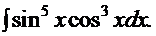
Рецепт. Используем преобразования, описанные выше, и получаем интеграл

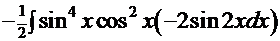 . Замена:
. Замена: 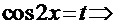
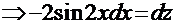 преобразует интеграл
преобразует интеграл 
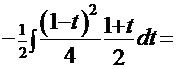
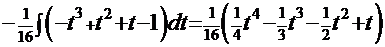 . После обратной подстановки имеем решение
. После обратной подстановки имеем решение 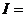
 .
.
Каждый из этих трёх вариантов решения требует своего подхода. Но есть ещё один приём:
г) «универсальная тригонометрическая подстановка»  , для которой находим дифференциал
, для которой находим дифференциал 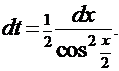 Отсюда
Отсюда 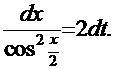 Применим этот приём к уже знакомому интегралу из Примера 11
Применим этот приём к уже знакомому интегралу из Примера 11 
 . Подставив введённые выше выражения для
. Подставив введённые выше выражения для 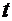 и
и 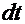 , получаем интеграл:
, получаем интеграл:  Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»:
Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»: 

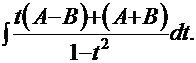 Решаем простую систему линейных уравнений:
Решаем простую систему линейных уравнений:  . Результат:
. Результат: 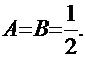 Продолжим решение интеграла:
Продолжим решение интеграла:  =
= 
 Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем
Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем  Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
N.B.! Имеются данные [1], что использование «универсальной подстановки» может привести к громоздким преобразованиям, что несколько снижает его ценность.
6.3. Интегралы типа 
Поверхностный взгляд на подынтегральные функции данной группы вызывает очевидные ассоциации с формулами  и
и  . Вспомним, что:
. Вспомним, что:

Рассмотрим для примера решение интеграла 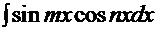 . Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет
. Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет 
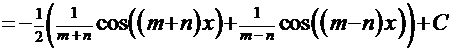 .
.
Аналогично решаются и остальные интегралы.
Пример 17. 
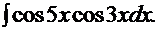
Рецепт. Применив одну из ранее приведённых формул, получаем решение:

 .
.
6.4. Интегралы типа 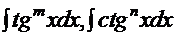
Такого рода интегралы сводятся к табличным интегралам простой подстановкой: 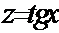 для первого интеграла и
для первого интеграла и 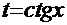 - для второго.
- для второго.
Пример 18. 
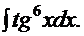
Рецепт. Используем замену 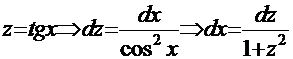 и получаем решение
и получаем решение 
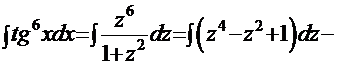
 =
= 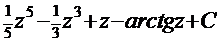 . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 
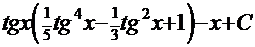 .
.
Пример 19. 
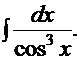
Рецепт. Ранее был рассмотрен интеграл  , поэтому данный интеграл решаем рассмотренным ранее методом «по частям»:
, поэтому данный интеграл решаем рассмотренным ранее методом «по частям»: 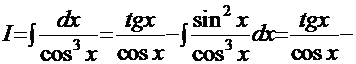

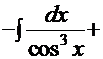
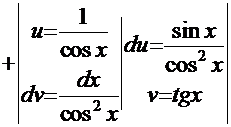
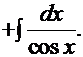 Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл
Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл 
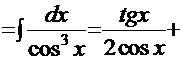

6.5. Интегралы типа 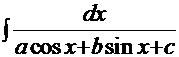 .
.
К таким интегралам наиболее эффективно (а зачастую – единственным образом) применение описанной выше «универсальной подстановки»: 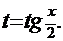
Вспомним, что  ,
, 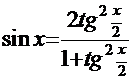 , и (см. стр. 16)
, и (см. стр. 16) 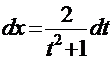 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 
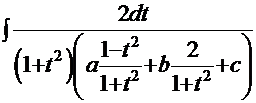 =
=  = =
= = 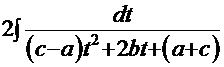 .
.
В зависимости от конкретного сочетания значений коэффициентов  получаем два основных исхода (с вариациями):
получаем два основных исхода (с вариациями):
1. 
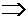 см. Пример 4.
см. Пример 4.
2. 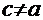 . Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя
. Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя 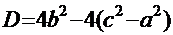 =
= 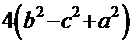 на два варианта:
на два варианта:
2а: 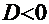 ─ см. Пример 3;
─ см. Пример 3;
2б: 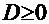 ─ см. Пример 9.
─ см. Пример 9.
Рассмотрим конкретный пример:
Пример 20. 
 .
.
Рецепт. Здесь  ,
, 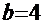 ,
,  ,
, 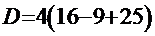 =
= 
 .
.
Согласно вышеприведённой формуле с использованием универсальной подстановки  данный интеграл получает вид
данный интеграл получает вид 
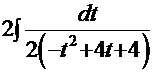 = =
= =  . Значение дискриминанта
. Значение дискриминанта 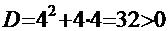 . Тогда корни трёхчлена знаменателя вычисляем по формуле
. Тогда корни трёхчлена знаменателя вычисляем по формуле 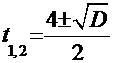 =
=  . В соответствии с методом «неопределённых коэффициентов»
. В соответствии с методом «неопределённых коэффициентов» 
 =
=
= 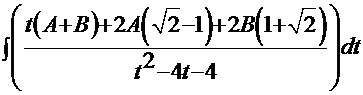 . Отсюда имеем систему двух линейных уравнений для коэффициентов
. Отсюда имеем систему двух линейных уравнений для коэффициентов  и
и 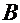 :
:  . Тогда
. Тогда 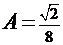 и
и 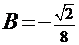 , а
, а 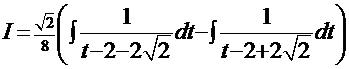 =
= 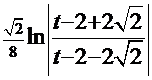 . Обратная подстановка
. Обратная подстановка  даёт конечный ответ
даёт конечный ответ 
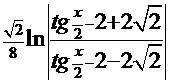 +С.
+С.



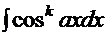 ,
, 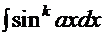 .
.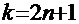 (нечётная степень):
(нечётная степень): 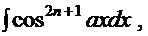
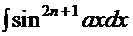
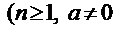
 . Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл
. Подход к этим интегралам одинаковый, поэтому сначала рассмотрим, например, интеграл 
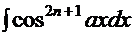 . Перепишем его в другой форме:
. Перепишем его в другой форме: 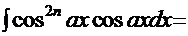
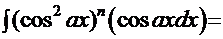
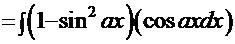 . Очевидна замена:
. Очевидна замена: 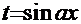



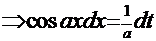 . Тогда
. Тогда 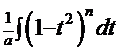 . После раскрытия скобок для соответствующего значения
. После раскрытия скобок для соответствующего значения 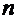 искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл
искомый интеграл приводится к алгебраической сумме интегралов от степенной функции. Аналогично решается и интеграл  с той лишь разницей, что заменяется
с той лишь разницей, что заменяется  .
.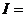

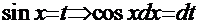 .
. 
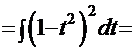
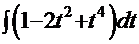 =
=  . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 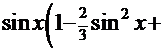
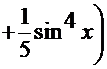

 (чётная степень):
(чётная степень):  .
.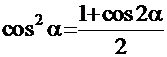 и
и 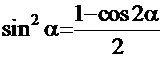 вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от
вдвое понижается степень и во столько же раз возрастает значение аргумента. Интеграл преобразуется в алгебраическую сумму интегралов от 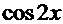 в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
в соответствующей степени (но отнюдь не обязательно!). Для интегралов с этой функцией в нечётной степени применяем способ из Примера 11, а для случая с чётной степенью – нужно ещё раз удвоить аргумент и т.д.
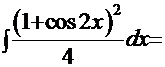
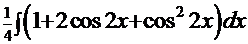


 .
.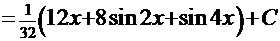
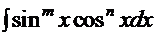
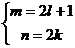 , либо
, либо  , где
, где  и
и 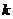 ─ целые числа.
─ целые числа.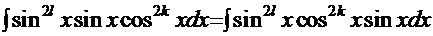 . Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену
. Вид последних двух сомножителей наводит на очевидную мысль, что необходимо ввести замену 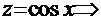
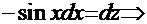
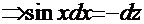 и воспользоваться основным тригонометрическим тождеством
и воспользоваться основным тригонометрическим тождеством 
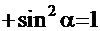 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 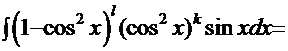
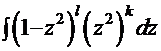 .
.
 и получаем
и получаем 
 . Обратная подстановка приводит к окончательному ответу
. Обратная подстановка приводит к окончательному ответу 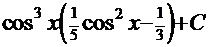 .
. . Тогда с помощью формул
. Тогда с помощью формул 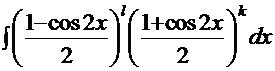 . Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
. Раскрываем скобки и получаем алгебраическую сумму табличных интегралов.
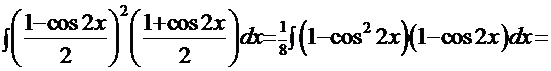
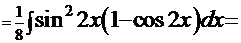
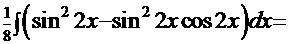

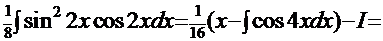
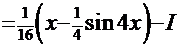 . Здесь
. Здесь  . Используем замену:
. Используем замену: 

 . Тогда
. Тогда 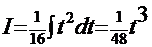 . Сделаем обратную подстановку и получим желанное решение:
. Сделаем обратную подстановку и получим желанное решение:  .
. . Тогда подынтегральная функция получит следующий вид:
. Тогда подынтегральная функция получит следующий вид:  =
= 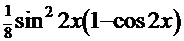 , а сам интеграл:
, а сам интеграл: 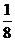
 =
= 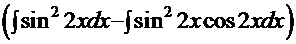 =
= 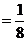
 -
- 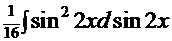 =
= 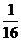
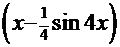 -
- 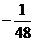
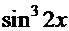 =
= 
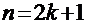 . Преобразуем интеграл к виду:
. Преобразуем интеграл к виду: 

 . Снова воспользуемся формулами удвоенного аргумента функции косинуса:
. Снова воспользуемся формулами удвоенного аргумента функции косинуса: 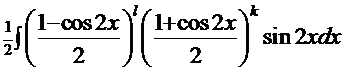 . Очевидно, что напрашивается замена:
. Очевидно, что напрашивается замена: 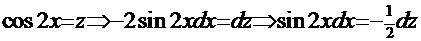 : тогда интеграл принимает вид:
: тогда интеграл принимает вид:  . Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.
. Снова интеграл доведён до состояния, когда его можно представить в виде алгебраической суммы табличных интегралов.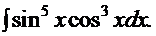
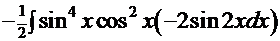 . Замена:
. Замена: 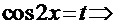
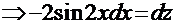 преобразует интеграл
преобразует интеграл 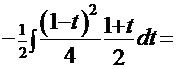
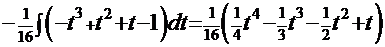 . После обратной подстановки имеем решение
. После обратной подстановки имеем решение  .
. , для которой находим дифференциал
, для которой находим дифференциал 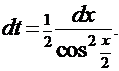 Отсюда
Отсюда 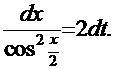 Применим этот приём к уже знакомому интегралу из Примера 11
Применим этот приём к уже знакомому интегралу из Примера 11 
 . Подставив введённые выше выражения для
. Подставив введённые выше выражения для 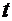 и
и 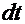 , получаем интеграл:
, получаем интеграл:  Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»:
Очевидно, что теперь можно использовать «метод неопределённых коэффициентов»: 

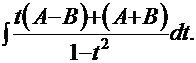 Решаем простую систему линейных уравнений:
Решаем простую систему линейных уравнений:  . Результат:
. Результат: 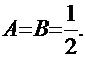 Продолжим решение интеграла:
Продолжим решение интеграла:  =
=  Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем
Возвращая этот результат в исходный интеграл и делая обратную подстановку, получаем  Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
Сравните этот результат с результатом Примера 11 и проверьте, нет ли расхождения.
 и
и  . Вспомним, что:
. Вспомним, что:
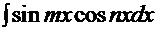 . Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет
. Для него подходит первая из этих формул. В результате такого преобразования решением этого интеграла будет 
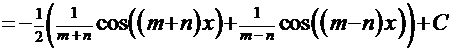 .
.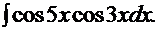
 .
.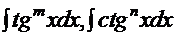
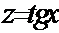 для первого интеграла и
для первого интеграла и 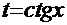 - для второго.
- для второго.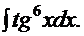
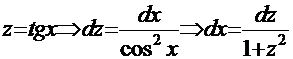 и получаем решение
и получаем решение 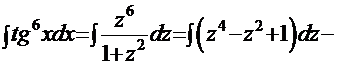
 =
= 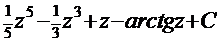 . После обратной подстановки получаем решение:
. После обратной подстановки получаем решение: 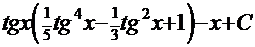 .
.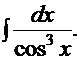
 , поэтому данный интеграл решаем рассмотренным ранее методом «по частям»:
, поэтому данный интеграл решаем рассмотренным ранее методом «по частям»: 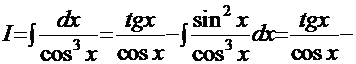

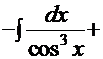
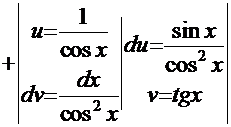
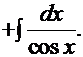 Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл
Нетрудно заметить, что мы снова имеем рекурсию. Отсюда искомый интеграл 
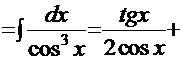

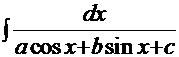 .
.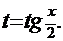
 ,
, 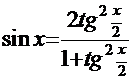 , и (см. стр. 16)
, и (см. стр. 16) 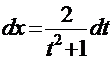 . Тогда интеграл примет вид:
. Тогда интеграл примет вид: 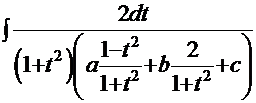 =
=  = =
= = 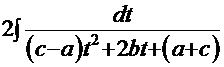 .
. получаем два основных исхода (с вариациями):
получаем два основных исхода (с вариациями):
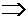 см. Пример 4.
см. Пример 4.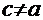 . Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя
. Этот случай, в свою очередь, распадается в зависимости от знака дискриминанта знаменателя 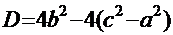 =
= 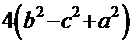 на два варианта:
на два варианта: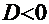 ─ см. Пример 3;
─ см. Пример 3;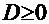 ─ см. Пример 9.
─ см. Пример 9. .
. ,
, 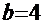 ,
,  ,
, 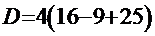 =
= 
 .
. данный интеграл получает вид
данный интеграл получает вид 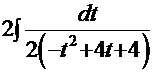 = =
= =  . Значение дискриминанта
. Значение дискриминанта 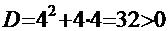 . Тогда корни трёхчлена знаменателя вычисляем по формуле
. Тогда корни трёхчлена знаменателя вычисляем по формуле 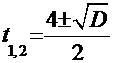 =
=  . В соответствии с методом «неопределённых коэффициентов»
. В соответствии с методом «неопределённых коэффициентов» 
 =
=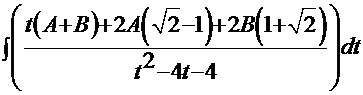 . Отсюда имеем систему двух линейных уравнений для коэффициентов
. Отсюда имеем систему двух линейных уравнений для коэффициентов  и
и 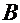 :
:  . Тогда
. Тогда 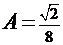 и
и 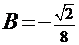 , а
, а 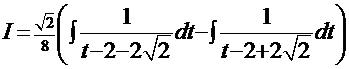 =
= 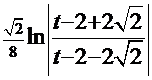 . Обратная подстановка
. Обратная подстановка 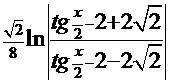 +С.
+С.

