Информационно-аналитическая модель для принятия решений по изменению облика и мощности МТС в условиях неопределенности

Под информационной моделью в данном исследовании по аналогии с [69, 80] понимается совокупность структурно-параметрических данных, критериев и ограничений, позволяющих оценить техническое состояние объекта исследования, показатели его работы и наметить альтернативы изменения его облика и мощности.

В нашем случае, рассматриваемая система S – МТЗ железнодорожное направление, которое может принимать на расчетный срок t_p конечное множество технических состояний: S₁, S₂, …, S_n с соответствующими «степенями возможности» (вероятностями) p(S₁), p(S₂), …, p(S_n), являющимися исходной информацией.

Исходная информация задается тремя формами представления, в зависимости от которых принимается критерий оптимального выбора, т.е. критерий цели. В соответствии с [79] различные критерии оптимального выбора являются следствием аксиомы рационального поведения, которая гласит: ЛПР выбирает решение так, чтобы максимизировать значение своего оценочного функционала.

В задачах принятия решений по изменению мощности применяются две группы критериев: критерии ресурсов и критерии цели. В данном исследовании для решения задачи изменения мощности МТС и ее элементов МТК, МТУ, МТЗ в условиях неопределенности технического состояния в качестве критериев ресурсов используется денежный критерий – капитальные вложения, а в качестве критериев цели используются три системы критериев – в зависимости от – формы задания исходной для расчетов информации:

1. Превышение наличной пропускной способности над потребной: – детерминированная форма задания исходной информации.

2. Вероятность непревышения потребной пропускной способности над наличной: P(N_п < N_н) [81] – вероятностно-определенная.

3. Превышение ожидаемой пропускной способности над потребной: – неопределенная.

Первая система критериев [69, 80] соответствует варианту, когда исходная информация о техническом состоянии всех элементов исследуемого МТЗ задается детерминировано.

1. Техническое состояние каждого перегона на расчетный срок t_p известно (или D={30;100}) – все вероятности p(S₁), p(S₂), …, p(S_n), обращаются в нуль, кроме одной – например p(S_К), которая равна единице.

2. Для состояния S_К, соответствующему , устанавливается параметр потока отказов для данного элемента МТЗ.

3. Наличная пропускная способность для МТЗ

, (3.8)

где - наличная пропускная способность на j-ом перегоне, ; m – количество элементов МТЗ.

4. Превышение наличной пропускной способности над потребной для МТЗ .

Вторая система критериев соответствует варианту, когда исходная информация о техническом состоянии всех элементов МТЗ задается в вероятностно-определенной форме.

1. Можно указать численные значения вероятностей возможных значений состояний S_i, соответствующих параметрам потока отказов w_i.

2. Для каждого элемента МТЗ оценивается его техническое состояние посредством математического ожидания наличной пропускной способности

(3.9)

где 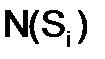– пропускная способность элементов МТЗ при условии реализации i-того состояния системы; – вероятность возникновения i-го состояния системы S_i.

Согласно рекомендациям [81], выполняются следующие действия:

5. Вероятность непревышения потребной пропускной способности

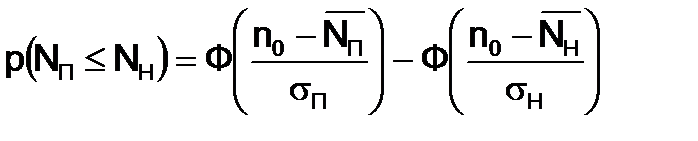, (3.10)

где , , – в данном исследовании принимаются заданными; 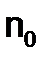– точка пересечения кривых плотности вероятности в соответствии с [81], значение которой находится из решения квадратного уравнения

,

,

,

. (3.11)

6. Вероятность непревышения потребной пропускной способности МТЗ

(3.12)

7. Математическое ожидание сокращения потерь времени в поездо-часах определяется по формуле

(3.13)

Математическое ожидание сокращения потерь времени в поездо-часах определяется для каждого перегона, то в целом для направления её можно рассчитать по формуле:

(3.14)

где М(t_потj) – математическое ожидание сокращения потерь времени в поездо-часах j-го перегона;

Третья система критериев соответствует варианту, когда исходная информация о техническом состоянии всех элементов исследуемого МТЗ задается в неопределенной форме и нет возможности выделить дискретные состояния S_i и их вероятности. Исходные данные характеризуются отрезками (диапазонами) DS_j.

Здесь различают три случая.

В первом случае, когда вероятность совпадения исходных данных с граничными значениями значительна, оценить техническое состояния можно в соответствии с максиминным критерием Вальда (в качестве оценочного функционала используется «выигрыш» – увеличение пропускной способности ) или критерием минимаксного риска Сэвиджа (оценочный функционал выражает риски ), «определяющий оптимальное решение, которое минимизирует риск, соответствующий наихудшей ситуации» [79]

1. Ожидаемая пропускная способность элемента определяется

(3.15)

где – число возможных значений состояний в j-м диапазоне DS_j; – число возможных диапазонов исходных данных DS.

Или

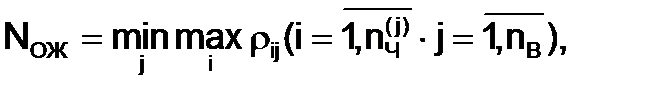(3.16)

(3.17)

где N_ij – пропускная способность в ситуации S_i и j-ом варианте диапазона DS_j.

2. Для состояния S_ОЖ, соответствующему , устанавливается параметр потока отказов для данного перегона.

3. Ожидаемая пропускная способность МТЗ:

, (3.18)

где 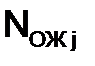– наличная пропускная способность на j-том перегоне, ;

4. Превышение ожидаемой пропускной способности над потребной для МТЗ: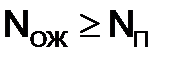

Во втором случае, если возможно указать степень предпочтения изменения исходной информации по границе максимальных (минимальных) возможных значений по сравнению с минимальной (максимальной) границей диапазона колебания, можно применить критерий пессимизма–оптимизма Гурвица, критерий «предлагает руководствоваться золотой серединой» между крайним пессимизмом и крайним оптимизмом» [79].

На этом основании:

1. Ожидаемая пропускная способность элемента МТЗ определяется:

(3.19)

где a – коэффициент, определяющий выбор веса пессимизма и оптимизма, изменяющийся в интервале .

При критерий Гурвица соответствует случаю крайнего оптимизма

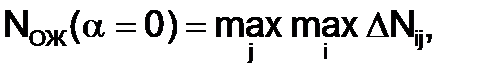(3.20)

При a=1 критерий Гурвица соответствует критерию пессимизма Вальда.

При устанавливается определенное соотношение между пессимизмом и оптимизмом

. (3.21)

Здесь a – показатель оптимизма, отражающий вероятность такого изменения исходной информации j-го варианта, которое соответствует максимальному значению оценочного функционала. Б.А. Волков [72] рекомендует в случае затруднения установки степени предпочтения при совпадении фактических значений показателей с одной из границ диапазона их возможного колебания показатель a принимать 0,3…0,4.

В случае, когда оценочный функционал выражает риски , критерий Гурвица можно записать в виде:

, (3.22)

При a=1 из формулы (3.20) можно получить критерий крайнего пессимизма Сэвиджа К_С, (3.21).

При a=0 получаем критерий крайнего оптимизма для рисков:

. (3.23)

2. Для состояния S_ОЖ, соответствующему , устанавливается параметр потока отказов для данного перегона.

3. Ожидаемая пропускная способность МТЗ: .

4. Превышение ожидаемой пропускной способности над потребной для МТЗ: .

При максимальной неопределенности (третий случай) [72] выбор следует производить в соответствии с максиминимальным превышением оценочного функционала, добиваясь тем самым путем минимизации степени риска получения большого проигрыша. Иными словами выбирается тот j-й вариант, который имеет максимальное значение . Минимальное превышение оценочного функционала для j-го его варианта может быть выражена зависимостью

. (3.24)

или выбирается тот вариант, который имеет минимальное значение

. (3.25)

Предложенные критерии позволяют определить неопределенность технического состояния железнодорожного направления и влияние энтропии на реальную мощность железнодорожного направления и качество его работы. Приведем разработанную информационно-ана­литическую модель (рис. 3.5) для принятия решений по изменению мощности МТЗ в условиях неопределенности его технического состояния.

Пример.

Требуется установить критерий цели в условиях той или иной степени неопределенности технического состояния элемента МТЗ m.

Рис. 3.5. Информационно-аналитическая модель для принятия решений по изменению мощности мультимодальной транспортной сети и/или ее элементов в условиях неопределенности их технического состояния

Математические модели и методы (Характеристика системы)

Детерминированная модель

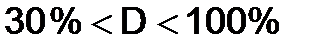
Вероятностно-определенная модель

Неопределенная модель

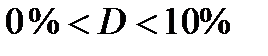
Область принимаемых решений

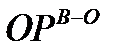
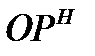
Критерии цели (эффективности)

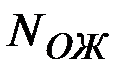
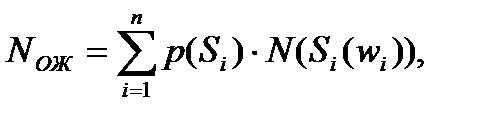
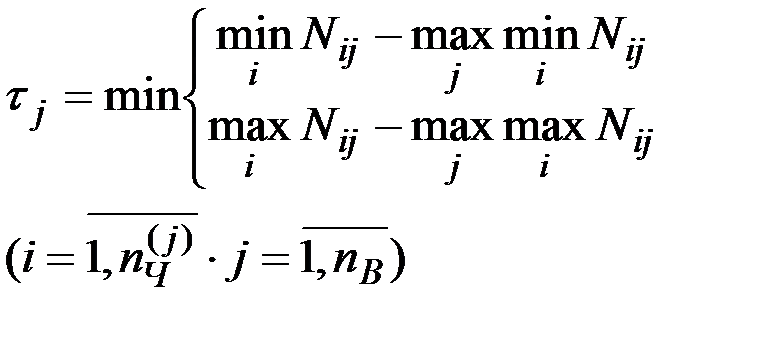
Наличная пропускная способность перегона на начальный момент времени – 39 пп/сутки.

В табл. 3.3 заданы исходные данные диапазоном возможных значений.

Таблица 3.3

Исходные данные

Возможные диапазоны	Наличная пропускная способность, пп/сутки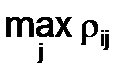
1-й вариант - DS1	36…32
2-й вариант - DS2	38…31
3-й вариант - DS3	41…34

 

Допустим, что не представляется возможным установить во всем диапазоне колебаний пропускной способности численные значения вероятностей, однако известно, что наиболее вероятные изменения пропускной способности будут следовать минимальной границе диапазона возможных значений. Выбор критерия цели проводится в соответствии с первым случаем неопределенной формы задания исходной информации, где используется критерий крайнего пессимизма Сэвиджа (3.15) или (3.16):

Для DS1: =7.

Для DS2: =8.

Для DS3: =5.

Т.к. = 5, оптимальным решением является 3-й вариант DS₃: 34пп/сутки.

Пусть известно, что изменение пропускной способности по границе минимальных значений по сравнению с совпадением фактическими значениями пропускной способности максимальной границы диапазона колебаний предпочтительнее (второй случай неопределенной формы задания исходной информации). Тогда показатель оптимизма принимается равным 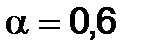. В соответствии с (3.19) получим:

Для DS1: пп/сутки.

Для DS2: пп/сутки.

Для DS3: пп/сутки.

Оптимальным решением является 1-й вариант DS₁: 33 пп/сутки.

В случае полной неопределенности по формуле (3.23) получим:

Для DS₁: .

Для DS₂: .

Для DS₃: .