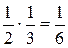Для функции f(x), интегрируемой для всех x ³a, значение интеграла 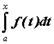 зависит от значения верхнего предела x; можно рассмотреть функцию переменной x: каждому значению x ставится в соответствие число, равное значению интеграла
зависит от значения верхнего предела x; можно рассмотреть функцию переменной x: каждому значению x ставится в соответствие число, равное значению интеграла 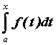 . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела:
. Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: 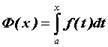 ; функция Ф(х) определена в области интегрируемости подынтегральной функции f(x),. Если F(x)первообразная для f(x), то значение Ф(х)можно вычислить по формуле Ньютона-Лейбница:
; функция Ф(х) определена в области интегрируемости подынтегральной функции f(x),. Если F(x)первообразная для f(x), то значение Ф(х)можно вычислить по формуле Ньютона-Лейбница:
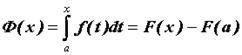 .
.
Функцию
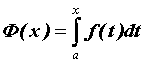
можно исследовать, не вычисляя первообразной. Для интегрируемой при x ³ a функции f(x), справедливы следующие утверждения: Ф(х)непрерывна на промежутке [a, ∞), причем Ф(а) = 0; если f(x)>0, при х ³ а, то Ф(х)монотонно возрастает на промежутке [a, ∞); если f(x), непрерывна при х ³ а, то Ф(х) дифференцируема на промежутке [a, ∞), причем
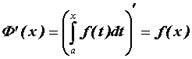
Замечание. То обстоятельство, что производная от интеграла с переменным верхним пределом есть подинтегральная функция, является одним из ключевых в математическом анализе. Это свойство интеграла с переменным верхним пределом является связующим звеном между дифференциальным и интегральным исчислением.
Отступление.
Несобственный интеграл
Пусть функция y = f (x) определена и непрерывна на полубесконечном промежутке [ a;¥), тогда интеграл 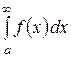 с бесконечным верхним пределом (несобственный интеграл) понимается как
с бесконечным верхним пределом (несобственный интеграл) понимается как 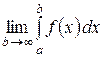 , если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
, если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
Аналогично
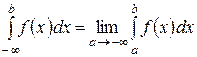 и
и 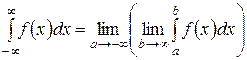
Функция распределения FХ (x) случайной величины Х имеет следующие свойства.
1. FХ (x) — непрерывная возрастающая функция.
2. 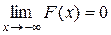 ;
; 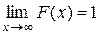
Свойства 1 и 2 вытекают непосредственно из определения функции F (x).
3. Приращение F (x) на промежутке (х 1; х 2) равно вероятности того, что случайная величина Х принимает значение из этого промежутка:
F (x 2) – F (x 1) = P (x 1 £Х < x 2)
Доказательство.
F (x 2) = P (Х < x 2) = P (Х < x 1) + P (x 1 £ Х < x 2) = F (x 1) + P (x 1 £Х < x 2)
Отсюда
P (x 1 £ Х < x 2) = F (x 2) – F (x 1)
Для равномерного распределения функция F (x) имеет вид:
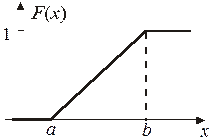
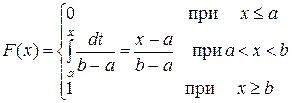
График функции F (x) представлен на рисунке 3.
Закон распределения непрерывной случайной величины можно определить заданием либо функции r (х), либо функции F (x).
Примеры абсолютно непрерывных распределений.
Равномерное непрерывное распределение было рассмотрено выше
Экспоненциальное распределение. Это распределение с плотностью ρ(х)=
 , λ > 0 – параметр экспоненциального распределения, его
, λ > 0 – параметр экспоненциального распределения, его
функция распределения имеет вид 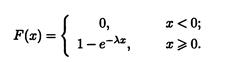
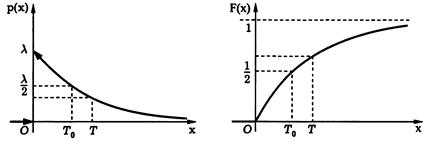
Плотность Функция распределения
Рис.4
Экспоненциальное распределение возникает как предельный вариант геометрического распределения. В качестве успехов и неудач рассматривается, произошло ли событие А в течение (стремящихся к нулю) промежутков времени.
Нормальное распределение.
Случайная величина имеет нормальный закон распределения c параметрами, m и σ2, N (m, σ2) если ее плотность имеет вид
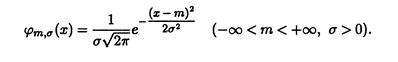
А функция распределения, соответственно,
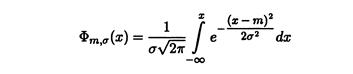
Если m=0, σ =1, распределение называется стандартным нормальным законом. Плотность в этом случае – уже известная функция Гаусса.
Поэтому в случае нормального закона плотность и функция распределения обозначаются φ и Ф, а не ρ и F.
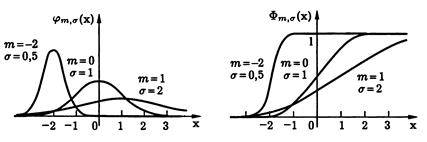
Рис. 5
Как следует из этих рисунков, параметр m определяет положение центра симметрии плотности нормального распределения, а σ – разброс значений случайной величины относительно центра симметрии. И, соответственно,
высоту и «крутизну» пика графика плотности (чем больше σ, тем ниже пик и медленнее стремление к нулю)
К абсолютно непрерывным распределениям относятся также крайне важные в статистической практике распределения χ2 и Стьюдента. Но ввиду сложности формул этих распределений (они содержат гамма-функцию Эйлера), мы не будем их здесь приводить.
Понятие случайного вектора.
В прикладных задачах часто приходится рассматривать не одну случайную величину, а несколько, наблюдаемых одновременно в эксперименте.
Определение. Совокупность случайных величин Х1, Х2, … Хn, заданных на одном и том же вероятностном пространстве (W, A, Р), называются n-мерным случайным вектором или n-мерной случайной величиной. Сами случайные величины называются при этом координатами случайного вектора.При n=2 случайная величина называется двумерной. Мы ограничимся рассмотрением этого случая.
Итак,
Пара случайных величин (X,Y) (или (ξ,η), заданных на одном вероятностном пространстве. называется двумерной случайной величиной (двумерным случайным вектором)
Когда речь идет о двух случайных величинах, мы можем интересоваться распределением каждой из них «самой по себе», а также условным распределением (одной, при условии, что вторая приняла какие-то значения).
Соответствующее распределение случайного вектора называется совместным распределением.
(Совместная) функция распределения F(a1,a2)= P{X< a1, Y< a2} в данном случае есть вероятность попасть в квадрант, верхним правым углом которого является точка (a1,a2)
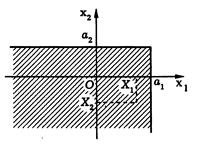
Рис.6
Определение. Двумерная величина (X,Y) называется дискретной, если дискретной является каждая из величин Х и Y. Мы ограничимся рассмотрением случая двумерной дискретной случайной величины.
Определение. Две случайные величины
Х = { x 1, x 2,¼, xn }; Y = { у 1, у 2,¼, уm },
определённые на одном и том же пространстве элементарных исходов, имеющие законы распределения
| X
| х 1
| ¼
| xi
| ¼
|
| Y
| y 1
| ¼
| yj
| ¼
|
| Р
| 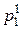
| ¼
| 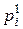
| ¼
|
| Р
| 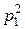
| ¼
| 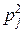
| ¼
|
(верхние индексы – это не степени, а указатель на принадлежность той или иной случайной величине)
называются независимыми, если при любых i и j выполняется равенство
Р ((X = хi) ∩ (Y = yj)) = 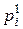
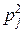
Замечание. В общем случае, случайные величины независимы, если совместная функция их распределения равна произведению функций распределения X и Y.
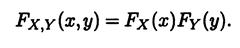
Или, в терминах вероятности, P(X<x, Y<y) = P(X<x) × P(Y<y)
Пример. Брошены две игральных кости. Число очков, выпавшее на первой кости, – случайная величина Х. Число очков, выпавшее на второй кости – случайная величина Y. Считаем, что все исходы ((X = i)∩(Y = j)) (i = 1,2,¼,6; j = 1,2, ¼,6) равновероятны, всего их 36 (см Тема 1), поэтому
P ((X = i)∩(Y = j)) = 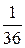
Так как P (X = i) = 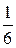 и P (Y = j)) =
и P (Y = j)) = 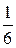 , очевидно, что по определению X и Y – независимые случайные величины.
, очевидно, что по определению X и Y – независимые случайные величины.
Пример 2. Даны две независимые случайные величины X и Y с заданными законами распределения
Определим случайные величины a и b следующим образом: a = X + Y, b = XY. Выясним, являются ли независимыми случайные величины a и b.
Составим закон распределения a.
| a
|
|
|
|
| b
|
|
|
|
| Р
| 1/12
| 2/12+3/12=5/12
| 6/12=1/2
|
| Р
| 1/12+3/12=1/3
| 2/12=1/6
| 6/12
|
Наименьшее значение a равняется 1. Вероятность события a = 1 равна вероятности события (X = 0)∩(Y = 1), которая в силу независимости X и Y равна 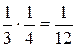 . Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
. Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
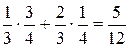 .
.
Максимальное значение a, равное 3, имеет вероятность 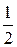 .
.
Рассмотрим события a = 3 и b = 0. Очевидно, что
Р (a = 3) Р (b = 0) = 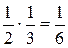
С другой стороны, событие (a = 3)∩(b = 0) – невозможное, так как a = 3 только при X = 1, а b = 0 лишь при X = 0. Отсюда следует, что
Р ((a = 3)∩(b = 0)) = 0,



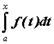 зависит от значения верхнего предела x; можно рассмотреть функцию переменной x: каждому значению x ставится в соответствие число, равное значению интеграла
зависит от значения верхнего предела x; можно рассмотреть функцию переменной x: каждому значению x ставится в соответствие число, равное значению интеграла 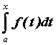 . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела:
. Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: 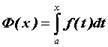 ; функция Ф(х) определена в области интегрируемости подынтегральной функции f(x),. Если F(x)первообразная для f(x), то значение Ф(х)можно вычислить по формуле Ньютона-Лейбница:
; функция Ф(х) определена в области интегрируемости подынтегральной функции f(x),. Если F(x)первообразная для f(x), то значение Ф(х)можно вычислить по формуле Ньютона-Лейбница: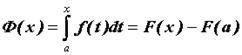 .
.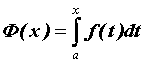
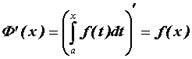
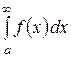 с бесконечным верхним пределом (несобственный интеграл) понимается как
с бесконечным верхним пределом (несобственный интеграл) понимается как 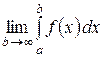 , если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
, если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.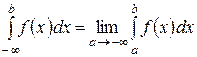 и
и 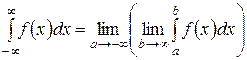
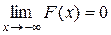 ;
; 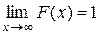

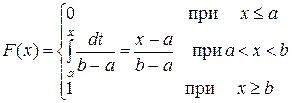
 , λ > 0 – параметр экспоненциального распределения, его
, λ > 0 – параметр экспоненциального распределения, его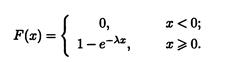

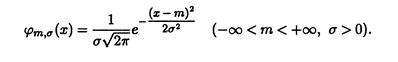
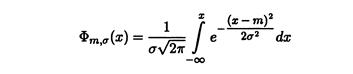


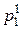
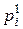
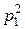
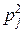
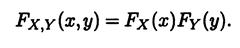
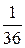
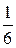 и P (Y = j)) =
и P (Y = j)) = 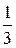
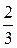
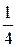
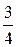
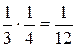 . Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
. Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна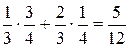 .
.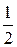 .
.