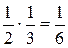Модуль 3.
Лекция 20.Случайные величины и функции распределения
Раздел 20.1.Понятие случайной величины.
Понятие случайной величины
Функция распределения случайной величины, ее свойства
Раздел 20.2.Случайные величины с дискретным распределением
Понятие случайной величины с дискретным распределением
Закон распределения дискретной случайной величины.
Примеры дискретных распределений
Раздел 20.3. Случайные величины с абсолютно непрерывным распределением
Понятие случайной величины с абсолютно непрерывным распределением
Закон распределения абсолютно непрерывной случайной величины. Плотность, ее свойства
Примеры абсолютно непрерывных распределений
Раздел 20.4.Понятие случайного вектора.
Понятие случайного вектора
Независимые случайные величины
Совместное распределение случайных величин
Программные положения
Понятие случайной величины является основным для теории вероятностей и математической статистики. Лекция содержит информацию об основных классах случайных величин – с дискретным и абсолютно непрерывным законами распределения, а также примеры основных табличных распределений. Также рассматривается вопрос о совместном распределении случайных величин и определение независимости.
Методические рекомендации
Перед изучением материала лекции вспомните определение функции и ее графика. Также вспомните определение независимых событий. Обратите внимание на формальное определение случайной величины. Заметьте, что для того, чтобы охарактеризовать случайную величину необходимо задать ее закон распределения и функцию распределения. Уделите особое внимание функции распределения и ее свойствам, поскольку именно в терминах этой функции формулируются задачи математической статистики. Обратите внимание на определение независимости случайных величин. Оно понадобится при изучении лекции 26, посвященной корреляционному анализу
Вопросы для самоконтроля
1. Что такое функция, ее область определения, множество значений?
Что такое пространство элементарных событий?
Что такое сигма-алгебра событий?
Дайте определение понятия случайной величины
Что такое случайные величины с дискретным и абсолютно непрерывным распределением?
Раздел 20.1. Понятие случайной величины.
С момента возникновения теории вероятностей ее основной задачей было изучение не вероятностных свойств экспериментов со случайными исходами, а связанных с этими экспериментами числовых величин, которые естественно назвать случайными величинами. Например, мы можем интересоваться не парами чисел на верхних гранях кубиков, а их суммой; числом успехов или числом неудач до первого успеха в схеме Бернулли.
Для того чтобы лучше осознать связь, существующую между случайными величинами и случайными событиями, начнем с пояснения понятия случайной величины. Случайной величиной естественно называть числовую величину, значение которой зависит от того, какой именно элементарный исход произошел в результате эксперимента со случайным исходом. Множество всех значений, которые случайная величина может принимать, называют множеством возможных значений этой случайной величины.
Следовательно, для задания случайной величины необходимо каждому элементарному исходу поставить в соответствие число — значение, которое примет случайная величина, если в результате испытания произойдет именно этот исход.
Часто в литературе можно встретить вариации на тему следующего определения: Случайной величиной называют переменную величину, которая в зависимости от исходов испытания принимает значения, зависящие от случая.
Таким образом, случайная величина – это числовая величина, значение которой зависит от того, какой именно (элементарный) исход произошел в результате эксперимента со случайным исходом. Множество всех значений, которые случайная величина может принимать, называют множеством возможных значений этой случайной величины.
Примеры 20.1.1
1) В опыте с однократным бросанием кубика: случайная величина принимает значения, равные числу, выпавшим на верхней грани (множество целых чисел то 1 до 6 для обычного кубика)
2) В опыте с однократным подбрасыванием двух кубиков: пространство элементарных событий – множество из 36 пар от (1,1) до (6,6), случайная величина каждой такой паре ставит в соответствие сумму ее составляющих. таким образом, эта случайная величина принимает множество (целых) значений от 2 до 12
Мы приведем более строгое определение, поскольку понятие случайной величины является одним из тех ключевых понятий, которые связывают теорию вероятностей с математическим анализом и составляют понятийную основу математической статистики.
Определение 20.1.1. Случайной величиной называется функция Х = Х(ω), определенная на пространстве элементарных событий Ω, для которых событие {Х < х} = {ω: Х(ω) < х} принадлежит σ-алгебре событий A для любого вещественного х.
Условие {Х < х} є A дает возможность рассматривать вероятности событий {Х < х}, поскольку вероятности определены только на множествах из А. Кроме того, через события {Х < х}, х є (-∞, ∞) с помощью известных операций над событиями можно выразить сколь угодно сложное событие, связанное со случайной величиной Х. Такое событие также будет принадлежать σ-алгебре событий A и, следовательно, для него определена вероятность.
Замечание 20.1.1. Таким образом, случайная величина – это функция, областью определения которой является пространство элементарных событий Ω, а множеством значений – числовое множество, возможно, все множество действительных чисел R.
σ-алгебра событий A – это область определения вероятности, если рассматривать ее как функцию.
Замечание 20.1.2.. «Термин «случайная величина» несколько неточен, более подходящим был бы термин «Функция случая», независимой переменной является точка в пространстве элементарных событий, т.е. исход эксперимента или случай». (В.Феллер «Введение в теорию вероятностей», гл. IX)
Случайные величины обозначаются буквами греческого алфавита: x (кси), h (эта), ¼ или заглавными буквами латинского алфавита X, Y, … Значения случайной величины будем записывать в виде конечной или бесконечной последовательности x 1, x 2,¼, xn,¼; y1, y2,¼, y n,¼
Замечание 20.1.2.. Ранее мы ввели понятие вероятности применительно к некоторым событиям. Теперь мы переходим к разговору о функциях. Самое очевидное событие, которое можно связать с понятием функции – это принятие ею некоторого значения (конкретного или принадлежащего промежутку)
Для исследования вероятностных свойств случайной величины необходимо знать правило, позволяющее находить вероятность того, что случайная величина примет значение из подмножества ее значений. Любое такое правило называют законом распределения вероятностей или распределением (вероятностей) случайной величины. (при этом слово «вероятностей» обычно опускают)
Общим законом распределения, присущим всем случайным величинам, является функция распределения.
Определение 20.1.2. Вся совокупность вероятностей Р{Х < х}, х є (-∞, ∞) задает закон распределения случайной величины Х в общем случае. Часто для краткости закон распределения случайной величины называют просто распределением случайной величины.
Определение20.1.3. Функция F(x) = Р{Х < х}, х є (-∞, ∞) называется функцией распределения случайной величины Х.
Значение функции распределения в точке х равно вероятности события {Х < х}, то есть события, состоящего из тех и только тех элементарных исходов ω, для которых Х < х.
Обычно говорят, что значение функции распределения в точке х равно вероятности того, что случайная величина Х примет значение, меньшее х.
Геометрически это означает следующее: F(x) – вероятность того, что случайная величина Х примет значение, которое изображается точкой на числовой прямой, расположенной слева от точки х.
Замечание 20.1.4.. Функцию распределения называют также интегральной функцией, или интегральным законом распределения случайной величины Х
Функция распределения обладает следующими свойствами:
1) 0≤ F(x)≤1 (т.к. по определению, функция распределения является вероятностью)
2) F(x1) ≤ F(x2) при x1 < x2 (т.е. F(x) – неубывающая функция)
3) lim F(x) = 0 при x → - ∞, lim F(x) = 1 при x → + ∞
4) P (x1 ≤ X ≤ x2) = F(x1) - F(x2)
5) F(x) – непрерывная слева функция, т.е. F(x) = F(x - 0), где F(x - 0) = lim F(y) при y → x - 0 (левосторонний предел)
Замечание 20.1.5. Для того, чтобы подчеркнуть, какой именно случайной величине принадлежит функция распределения F(x), этой функции иногда приписывают нижний индекс, обозначающий конкретную случайную величину. Например, FX(x) = Р{Х < х}
Замечание 20.1.6. В некоторых изданиях функция распределения определяется как F(x) = Р{Х ≤ х}. Такое определение ничего не меняет по существу понятия функции распределения, меняется лишь последнее, пятое свойство. Функция в таком случае оказывается непрерывной справа.
Примеры дискретных распределений
Равномерное распределение
Дискретная величина принимает конечное число значений с одинаковыми вероятностями. Например, случайная величина принимает значение числа на верхней грани кубика при однократном подбрасывании
Биномиальное распределение
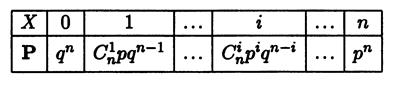
Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний.p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1
P{X =i} = 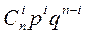
Сумма в нижней строке есть биномиальное разложение для (p+q)n = 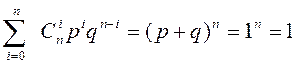
Распределение Пуассона
Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний: Х=0,1,2,…,n…, p – вероятность успеха, успехи редки, их вероятность мала. n∙p=λ>0 – параметр распределения

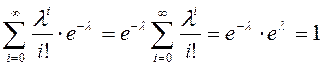
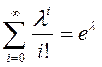 - сумма ряда Тейлора для экспоненты
- сумма ряда Тейлора для экспоненты
Отступление.
Отступление.
Несобственный интеграл
Пусть функция y = f (x) определена и непрерывна на полубесконечном промежутке [ a;¥), тогда интеграл 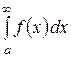 с бесконечным верхним пределом (несобственный интеграл) понимается как
с бесконечным верхним пределом (несобственный интеграл) понимается как 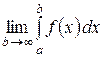 , если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
, если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
Аналогично
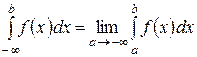 и
и 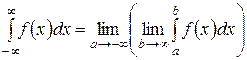
Функция распределения FХ (x) случайной величины Х имеет следующие свойства.
1. FХ (x) — непрерывная возрастающая функция.
2. 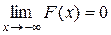 ;
; 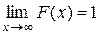
Свойства 1 и 2 вытекают непосредственно из определения функции F (x).
3. Приращение F (x) на промежутке (х 1; х 2) равно вероятности того, что случайная величина Х принимает значение из этого промежутка:
F (x 2) – F (x 1) = P (x 1 £Х < x 2)
Доказательство.
F (x 2) = P (Х < x 2) = P (Х < x 1) + P (x 1 £ Х < x 2) = F (x 1) + P (x 1 £Х < x 2)
Отсюда
P (x 1 £ Х < x 2) = F (x 2) – F (x 1)
Для равномерного распределения функция F (x) имеет вид:
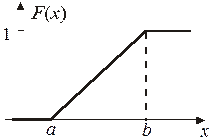
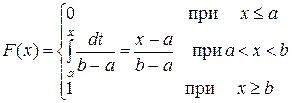
График функции F (x) представлен на рисунке 3.
Закон распределения непрерывной случайной величины можно определить заданием либо функции r (х), либо функции F (x).
Примеры абсолютно непрерывных распределений.
Равномерное непрерывное распределение было рассмотрено выше
Экспоненциальное распределение. Это распределение с плотностью ρ(х)=
 , λ > 0 – параметр экспоненциального распределения, его
, λ > 0 – параметр экспоненциального распределения, его
функция распределения имеет вид 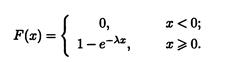
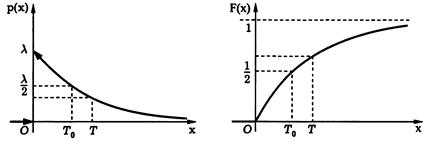
Плотность Функция распределения
Рис.4
Экспоненциальное распределение возникает как предельный вариант геометрического распределения. В качестве успехов и неудач рассматривается, произошло ли событие А в течение (стремящихся к нулю) промежутков времени.
Нормальное распределение.
Случайная величина имеет нормальный закон распределения c параметрами, m и σ2, N (m, σ2) если ее плотность имеет вид
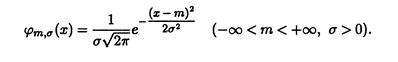
А функция распределения, соответственно,
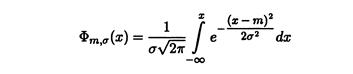
Если m=0, σ =1, распределение называется стандартным нормальным законом. Плотность в этом случае – уже известная функция Гаусса.
Поэтому в случае нормального закона плотность и функция распределения обозначаются φ и Ф, а не ρ и F.
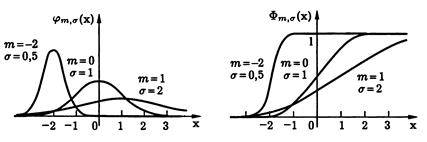
Рис. 5
Как следует из этих рисунков, параметр m определяет положение центра симметрии плотности нормального распределения, а σ – разброс значений случайной величины относительно центра симметрии. И, соответственно,
высоту и «крутизну» пика графика плотности (чем больше σ, тем ниже пик и медленнее стремление к нулю)
К абсолютно непрерывным распределениям относятся также крайне важные в статистической практике распределения χ2 и Стьюдента. Но ввиду сложности формул этих распределений (они содержат гамма-функцию Эйлера), мы не будем их здесь приводить.
Понятие случайного вектора.
В прикладных задачах часто приходится рассматривать не одну случайную величину, а несколько, наблюдаемых одновременно в эксперименте.
Определение. Совокупность случайных величин Х1, Х2, … Хn, заданных на одном и том же вероятностном пространстве (W, A, Р), называются n-мерным случайным вектором или n-мерной случайной величиной. Сами случайные величины называются при этом координатами случайного вектора.При n=2 случайная величина называется двумерной. Мы ограничимся рассмотрением этого случая.
Итак,
Пара случайных величин (X,Y) (или (ξ,η), заданных на одном вероятностном пространстве. называется двумерной случайной величиной (двумерным случайным вектором)
Когда речь идет о двух случайных величинах, мы можем интересоваться распределением каждой из них «самой по себе», а также условным распределением (одной, при условии, что вторая приняла какие-то значения).
Соответствующее распределение случайного вектора называется совместным распределением.
(Совместная) функция распределения F(a1,a2)= P{X< a1, Y< a2} в данном случае есть вероятность попасть в квадрант, верхним правым углом которого является точка (a1,a2)
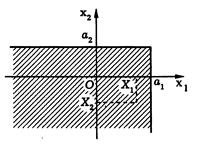
Рис.6
Определение. Двумерная величина (X,Y) называется дискретной, если дискретной является каждая из величин Х и Y. Мы ограничимся рассмотрением случая двумерной дискретной случайной величины.
Определение. Две случайные величины
Х = { x 1, x 2,¼, xn }; Y = { у 1, у 2,¼, уm },
определённые на одном и том же пространстве элементарных исходов, имеющие законы распределения
| X
| х 1
| ¼
| xi
| ¼
|
| Y
| y 1
| ¼
| yj
| ¼
|
| Р
| 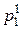
| ¼
| 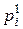
| ¼
|
| Р
| 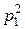
| ¼
| 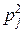
| ¼
|
(верхние индексы – это не степени, а указатель на принадлежность той или иной случайной величине)
называются независимыми, если при любых i и j выполняется равенство
Р ((X = хi) ∩ (Y = yj)) = 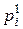
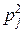
Замечание. В общем случае, случайные величины независимы, если совместная функция их распределения равна произведению функций распределения X и Y.
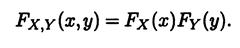
Или, в терминах вероятности, P(X<x, Y<y) = P(X<x) × P(Y<y)
Пример. Брошены две игральных кости. Число очков, выпавшее на первой кости, – случайная величина Х. Число очков, выпавшее на второй кости – случайная величина Y. Считаем, что все исходы ((X = i)∩(Y = j)) (i = 1,2,¼,6; j = 1,2, ¼,6) равновероятны, всего их 36 (см Тема 1), поэтому
P ((X = i)∩(Y = j)) = 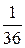
Так как P (X = i) = 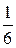 и P (Y = j)) =
и P (Y = j)) = 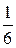 , очевидно, что по определению X и Y – независимые случайные величины.
, очевидно, что по определению X и Y – независимые случайные величины.
Пример 2. Даны две независимые случайные величины X и Y с заданными законами распределения
Определим случайные величины a и b следующим образом: a = X + Y, b = XY. Выясним, являются ли независимыми случайные величины a и b.
Составим закон распределения a.
| a
|
|
|
|
| b
|
|
|
|
| Р
| 1/12
| 2/12+3/12=5/12
| 6/12=1/2
|
| Р
| 1/12+3/12=1/3
| 2/12=1/6
| 6/12
|
Наименьшее значение a равняется 1. Вероятность события a = 1 равна вероятности события (X = 0)∩(Y = 1), которая в силу независимости X и Y равна 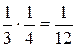 . Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
. Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
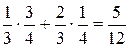 .
.
Максимальное значение a, равное 3, имеет вероятность 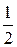 .
.
Рассмотрим события a = 3 и b = 0. Очевидно, что
Р (a = 3) Р (b = 0) = 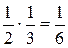
С другой стороны, событие (a = 3)∩(b = 0) – невозможное, так как a = 3 только при X = 1, а b = 0 лишь при X = 0. Отсюда следует, что
Р ((a = 3)∩(b = 0)) = 0,
Пример.
Рассмотрим коробку, в которой лежат две карточки с цифрой 1 и три карточки с цифрой 2. Одна за другой вынимаются две карточки. X – номер на первой карточке. Y – на второй. Найти совместный закон распределения (X,Y)
Используем формулу произведения вероятностей P((X,Y)=(1,1)) = P(X=1)P(Y=1|X=1)=2/5× ¼ = 1/10
| (X,Y)
| (1,1)
| (1,2)
| (2,1)
| (2,2)
|
| P
| 1/10
| 3/10
| 3/10
| 3/10
|
Сумма вероятностей = 1.
Модуль 3.
Лекция 20.Случайные величины и функции распределения




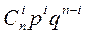

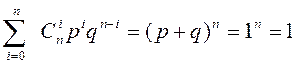

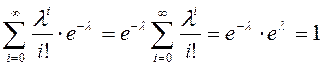
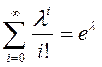 - сумма ряда Тейлора для экспоненты
- сумма ряда Тейлора для экспоненты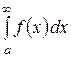 с бесконечным верхним пределом (несобственный интеграл) понимается как
с бесконечным верхним пределом (несобственный интеграл) понимается как 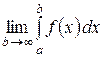 , если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
, если этот предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.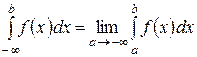 и
и 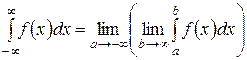
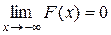 ;
; 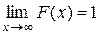

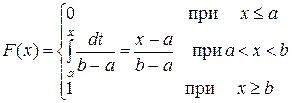
 , λ > 0 – параметр экспоненциального распределения, его
, λ > 0 – параметр экспоненциального распределения, его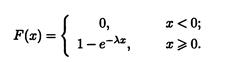

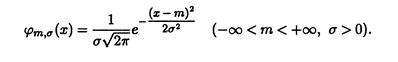
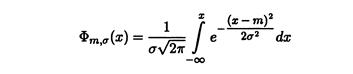


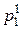
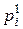
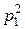
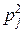
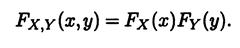
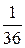
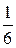 и P (Y = j)) =
и P (Y = j)) = 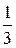
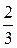
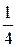
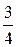
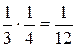 . Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна
. Событие a = 2 совпадает с событием ((X = 0)∩(Y = 2)) + ((X = 1)∩(Y = 1)). Его вероятность равна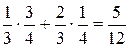 .
.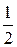 .
.