Методом сил
Рассмотрим алгоритм расчета статически неопределимых систем на примере рамы, показанной на рисунке 3.30, а. В качестве примера выбрана достаточно простая система, позволяющая не перегружать расчет арифметическими выкладками, но в то же время показать особенности расчета, характерные и для более сложных систем.
Установление степени статической неопределимости. Для рассматриваемой системы степень статической неопределимости n = 3.
Выбор основной системы. Для выбора основной системы необходимо в заданной системе удалить три лишних связи. При этом получаемая основная система должна быть статически определимой и геометрически неизменяемой.
Заданная система является симметричной конструкцией, на которую действует симметричная нагрузка. Поэтому целесообразно выбирать симметричную основную систему.
Рассматриваемая система три раза статически неопределима, но условия симметрии конструкции и загружения позволяют сократить число лишних неизвестных до двух (правило 3).
Основную систему получаем рассечением стержня по оси симметрии и введением в местах разреза реакций удаленных связей – симметричных силовых факторов Х 1 и Х 2 (рисунок 3.30, б). Кососимметричный силовой фактор Х 3 (поперечная сила) в плоскости симметрии будет равен нулю.
П р и м е ч а н и е – Направление действия реакций отброшенных связей принимают произвольно.
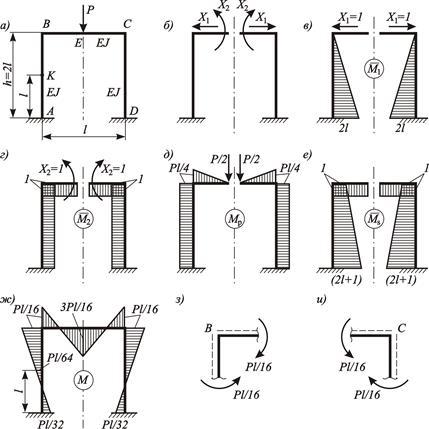
Рисунок 3.30 – К расчету статически неопределимой системы:
а – исходная система; б – основная система; в, г – единичные эпюры моментов;
д – грузовая эпюра моментов; е – суммарная единичная эпюра моментов;
ж – окончательная эпюра моментов; з, и – вырезанные узлы
Составление канонических уравнений. Для двух неизвестных система канонических уравнений будет иметь вид:
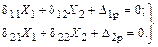
Определение коэффициентов и свободных членов канонических уравнений. Для вычисления коэффициента 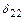 и свободного члена
и свободного члена 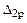 :
:
1) строим эпюры изгибающих моментов: единичные 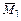 ,
, 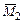 (от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую
(от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую 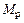 (от внешней нагрузки Р);
(от внешней нагрузки Р);
2) перемножаем эпюры по формулам, приведенным в п. 3.5.
П р и м е ч а н и е – Для упрощения расчета ограничимся рассмотрением только эпюр изгибающих моментов.
При построении эпюр основную систему поочередно нагружаем усилиями Х 1 = 1, Х 2 = 1 и внешней нагрузкой Р. Построенные эпюры моментов 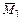 ,
, 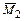 и
и 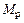 приведены на рисунках 3.30, в–д.
приведены на рисунках 3.30, в–д.
Тогда:
коэффициент 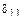 (результат перемножения эпюры
(результат перемножения эпюры 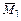 саму на себя)
саму на себя)
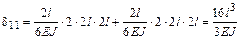 ;
;
коэффициент 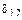 (результат перемножения эпюр
(результат перемножения эпюр 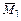 и
и 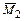 )
)
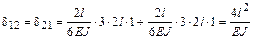 ;
;
коэффициент 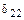 (результат перемножения эпюры
(результат перемножения эпюры 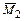 саму на себя)
саму на себя)
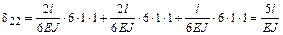 ;
;
свободный член 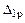 (результат перемножения эпюр
(результат перемножения эпюр 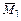 и
и 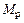 )
)
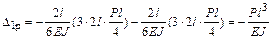 ;
;
свободный член 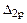 (результат перемножения эпюр
(результат перемножения эпюр 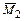 и
и 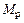 )
)
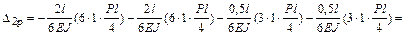
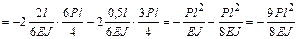 .
.
Для контроля правильности определения коэффициентов и свободных членов строим суммарную единичную эпюру 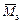 (рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
(рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
Перемножаем суммарную эпюру саму на себя (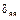 ) и на грузовую (
) и на грузовую (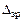 ):
):
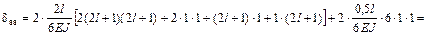
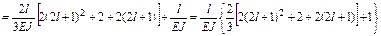 ;
;
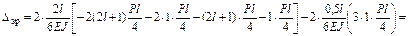
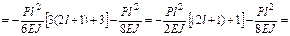
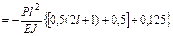 .
.
Проверку коэффициентов и свободных членов выполним для l = 1 м.
Тогда
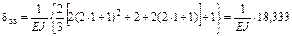 ;
;
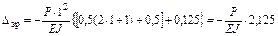 .
.
Определяем:
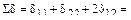
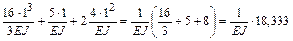 .
.
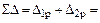
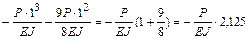 .
.
Поскольку 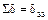 и
и 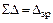 , коэффициенты и свободные члены определены правильно.
, коэффициенты и свободные члены определены правильно.
Решение канонических уравнений. Система канонических уравнений имеет вид:
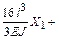
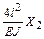
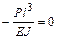 ;
;
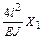
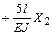
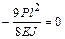 .
.
Умножая все уравнения на EJ, получим коэффициенты и свободные члены окончательной системы канонических уравнений:
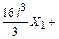
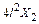
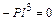 ;
;
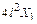
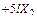
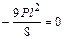 .
.
Решая канонические уравнения, находим значения неизвестных: 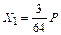 ,
, 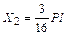 .
.
Для проверки правильности вычисления неизвестных подставляем найденные значения Х 1 и Х 2 в канонические уравнения:
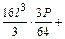
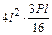
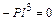 ;
;
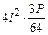
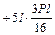
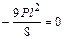 .
.
Построение окончательной эпюры моментов для заданной системы. Ординаты окончательной эпюры изгибающих моментов определяем по формуле (3.18).
Для построения окончательной эпюры изгибающих моментов ординаты единичных эпюр 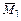 и
и 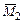 умножаем на соответствующие значения лишних неизвестных
умножаем на соответствующие значения лишних неизвестных 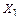 и
и 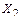 и складываем с ординатами грузовой эпюры
и складываем с ординатами грузовой эпюры 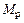 . Суммирование ординат производим по характерным точкам (А, В, С, D, Е) рамы:
. Суммирование ординат производим по характерным точкам (А, В, С, D, Е) рамы:
стержень (стойка) АВ –
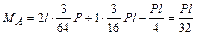 ;
;
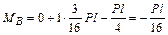 ;
;
стержень (ригель) ВС –
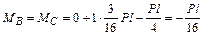 ;
;
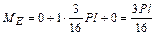 ;
;
стержень (стойка) С D –
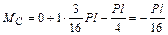 ;
;
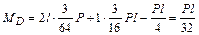 .
.
П р и м е ч а н и е – При вычислении ординат окончательной эпюры 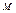 необходимо учитывать знаки силовых факторов
необходимо учитывать знаки силовых факторов 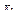 и
и 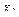 и моментов
и моментов 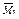 ,
, 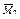 и
и 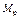 . Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
. Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
Окончательная эпюра изгибающих моментов показана на рисунке 3.30, ж).

 Производим проверку правильности построения окончательной эпюры М – статическую и кинематическую.
Производим проверку правильности построения окончательной эпюры М – статическую и кинематическую.
Для выполнения статической проверки вырезаем жесткие узлы рамы (кроме опорных), прикладываем все действующеие в них моменты и проверяем условие равновесия узла 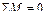 .
.
В рассматриваем случае вырезаем узлы В и С (рисунки 3.30, з, и):
узел В: 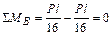 ;
;
узел С: 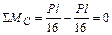 .
.
П р и м е ч а н и е – Знак ординаты эпюры М определяется стрелкой дуги окружности около узла, направленной так, чтобы вызвать растяжение в элементе со стороны ординат эпюры моментов.
Выполнение условия равновесия узлов является необходимым, но недостаточным.
Достаточным условием правильности построения окончательной эпюры М является кинематическая проверка по условию (3.19).
Для этого перемножим окончательную М и суммарную единичную 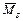 эпюры:
эпюры:
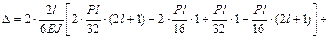
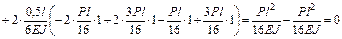 .
.
Поскольку 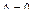 , условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.
, условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.






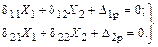
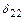 и свободного члена
и свободного члена 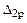 :
: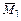 ,
, 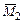 (от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую
(от неизвестных единичных силовых факторов Х 1 и Х 2) и грузовую 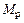 (от внешней нагрузки Р);
(от внешней нагрузки Р);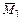 ,
, 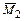 и
и 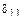 (результат перемножения эпюры
(результат перемножения эпюры 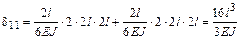 ;
;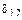 (результат перемножения эпюр
(результат перемножения эпюр 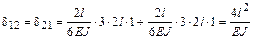 ;
;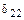 (результат перемножения эпюры
(результат перемножения эпюры 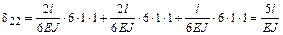 ;
;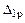 (результат перемножения эпюр
(результат перемножения эпюр 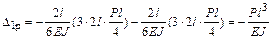 ;
;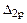 (результат перемножения эпюр
(результат перемножения эпюр 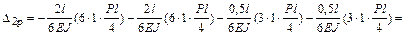
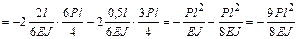 .
.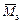 (рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).
(рисунок 3.30, е). Она представляет собой сумму эпюр от всех единичных неизвестных (см. формулу (3.15)).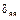 ) и на грузовую (
) и на грузовую (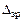 ):
):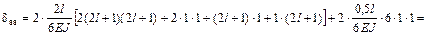
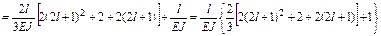 ;
;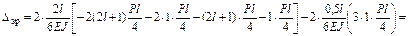
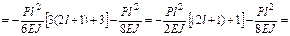
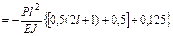 .
.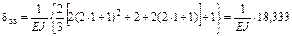 ;
;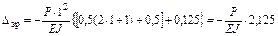 .
.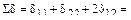
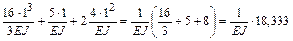 .
.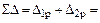
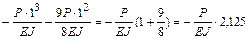 .
.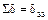 и
и 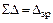 , коэффициенты и свободные члены определены правильно.
, коэффициенты и свободные члены определены правильно.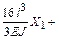
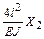
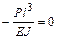 ;
;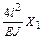
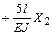
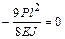 .
.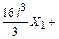
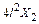
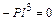 ;
;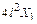
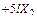
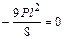 .
.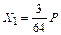 ,
, 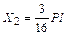 .
.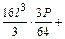
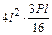
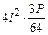
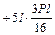
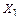 и
и 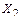 и складываем с ординатами грузовой эпюры
и складываем с ординатами грузовой эпюры 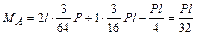 ;
;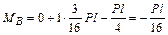 ;
;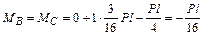 ;
;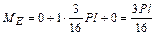 ;
;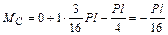 ;
;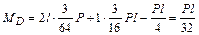 .
.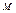 необходимо учитывать знаки силовых факторов
необходимо учитывать знаки силовых факторов 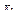 и
и 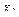 и моментов
и моментов 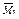 ,
, 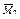 и
и 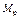 . Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
. Для этого задаемся правилом знаков изгибающих моментов: положительными считаем ординаты, расположенные внутрь рамы.
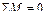 .
.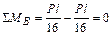 ;
;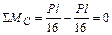 .
.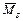 эпюры:
эпюры: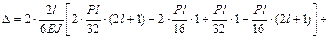
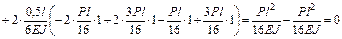 .
.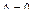 , условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.
, условие (3.19) выполняется. Это свидетельствует о правильности построения окончательной эпюры моментов М.


