МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По проведению практических (семинарских) занятий
по дисциплине (модулю)
«Математическая статистика»
основной профессиональной образовательной программы
высшего образования – программы бакалавриата
по направлению подготовки
09.03.01 «Информатика и вычислительная техника»
с профилем
«Электронно-вычислительные машины, комплексы, системы и сети»
Формы обучения: очная, заочная
Идентификационный номер образовательной программы: 090301-02-20
Тула 2020 год
Разработчик(и) методических указаний
____ Набродова И.Н., доцент, к.т.н. ____________ _______________
(ФИО, должность, ученая степень, ученое звание) (подпись)
Оглавление
Практическая работа №1. 4
Выборочный метод. 4
Практическая работа №2. 8
Оценка параметров распределений. 8
Практическая работа №3. 17
Проверка статистических гипотез. 17
Практическая работа №4. 26
Числовые характеристики случайных величин. 26
Практическая работа №5. 40
Элементы теории корреляции. 40
Список литературы.. 54
Практическая работа №1
Выборочный метод
Цель и задачи работы
Целью практической работы является изучение основных методов обработки данных, представленных выборкой, путем построения гистограммы.
Порядок выполнения работы
- ознакомится с теоретическими сведениями;
- выполнить задание;
- оформить отчет;
- ответить на контрольные вопросы, заданные преподавателем.
Оформление отчета
Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.
Теоретические сведения
Пусть для изучения количественного (дискретного или непрерывного) признака X из генеральной совокупности извлечена выборка x1, x2,..., x k объема n. Наблюдавшиеся значения xi признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом.
Статистическим распределением выборки называют перечень вариант xiвариационного ряда и соответствующих им частот ni (сумма всех частот равна объему выборки n)или относительных частот w ωi(сумма всех относительных частот равна единице). Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал).
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(х), определяющую для каждого значения x относительную частоту события X<х:
F*(x) = nx/n,
где nх – число вариант, меньших х, n – объем выборки.
Эмпирическая функция обладает следующими свойствами.
Свойство 1. Значения эмпирической функции принадлежат отрезку [0; 1].
Свойство 2. F*(х) – неубывающая функция.
Свойство 3. Если x1 – наименьшая варианта, а хk – наибольшая, то F*(x) = 0 при x ≤ x1 и F*(x) = l при х > хk.
Дискретное распределение признака X. Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1) (х2, n2), … (хk, nk), где xi –варианты выборки и ni – соответствующие им частоты.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1, ω1), (х2, ω2), …, (хk, ωk), где xi – варианты выборки и ωk – соответствующие им относительные частоты.
Непрерывное распределение признака X. При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины h и находят ni – сумму частот вариант, попавших в 1-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/h (плотность частоты). Площадь частичного i-гo прямоугольника равна h(ni/h) = ni – сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т. е. объему выборки n.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ωi/h (плотность относительной частоты). Площадь частичного 1-го прямоугольника равна h(ωi/h) = ωi – относительной частоте вариант, попавших в 1-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.
Оборудование
Персональный компьютер с установленной операционной системой Windows XP/7/8, браузер (Например, Internet Explorer, Google Chrome, Opera), текстовый редактор OOo Writer (MS Word), пакет офисных приложений «Мой офис».
Задание на работу
1. Выборка задана в виде распределения частот:
Найти распределение относительных частот.
2. Найти эмпирическую функцию по данному распределению выборки:
3. Найти эмпирическую функцию по данному распределению выборки:
4. Построить полигон частот по данному распределению выборки:
5. Построить полигон частот по данному распределению выборки:
| xi
| 15
| 20
| 25
| 30
| 35
|
| ni
| 10
| 15
| 30
| 20
| 25
|
6. Построить гистограмму частот по данному распределению выборки:
| Номер интервала, i
| Частичный интервал, xi–xi+1
| Сумма частот вариант интервала, ni
| Плотность частоты, ni/h
|
| 1
| 2-7
| 5
|
|
| 2
| 7-12
| 10
|
|
| 3
| 12-17
| 25
|
|
| 4
| 17-22
| 6
|
|
| 5
| 22-27
| 4
|
|
7. Построить гистограмму частот по данному распределению выборки:
| Номер интервала, i
| Частичный интервал, xi–xi+1
| Сумма частот вариант интервала, ni
| Плотность частоты, ni/h
|
| 1
| 3-5
| 4
|
|
| 2
| 5-7
| 6
|
|
| 3
| 7-9
| 20
|
|
| 4
| 9-11
| 40
|
|
| 5
| 11-13
| 20
|
|
| 6
| 13-15
| 4
|
|
| 7
| 15-17
| 6
|
|
8. Построить гистограмму относительных частот по данному распределению выборки:
| Номер интервала, i
| Частичный интервал, xi–xi+1
| Сумма частот вариант интервала, ni
|
| 1
| 10-15
| 2
|
| 2
| 15-20
| 4
|
| 3
| 20-25
| 8
|
| 4
| 25-30
| 4
|
| 5
| 30-35
| 2
|
9. Построить гистограмму относительных частот по данному распределению выборки:
| Номер интервала, i
| Частичный интервал, xi–xi+1
| Сумма частот вариант интервала, ni
|
| 1
| 2-5
| 6
|
| 2
| 5-8
| 10
|
| 3
| 8-11
| 4
|
| 4
| 11-14
| 5
|
7. Контрольные вопросы
1. Что является предметом изучения математической статистики?
2. Что такое статистические данные?
3. Какие основные задачи решает математическая статистика?
4. Что такое генеральная и выборочная совокупности?
5. Какие существуют способы образования выборки?
6. Графики статистического распределения: полигон и гистограмма.
7. Как задаётся эмпирическая функция распределения?
Практическая работа № 2
Цель и задачи работы
Целью практической работы является получения навыков при решении задач использования оценки параметров распределений: смещенных и несмещенных, различными методами.
Порядок выполнения работы
- ознакомится с теоретическими сведениями;
- выполнить задание;
- оформить отчет;
- ответить на контрольные вопросы, заданные преподавателем.
Оформление отчета
Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.
Теоретические сведения
Статистической оценкой Θ* неизвестного параметра Θ в теоретического распределения называют функцию f(X1, X2,..., Хn) от наблюдаемых случайных величин X1, X2,..., Хn
Точечной называют статистическую оценку, которая определяется одним числом Θ* = f(x 1, x 2,..., xn), где x1, х2,.... х n –результаты n наблюдений над количественным признаком X (выборка).
Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:
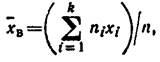
где xi – варианта выборки, ni – частота варианты xi, 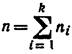 – объем выборки.
– объем выборки.
Замечание 1. Если первоначальные варианты xi – большие числа, то для упрощения расчета целесообразно вычесть из каждой варианты одно и то же число С, т. е. перейти к условным вариантам ui=xi–C (в качестве С выгодно принять число, близкое к выборочной средней; поскольку выборочная средняя неизвестна, число С выбирают «на глаз»). Тогда 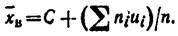
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:
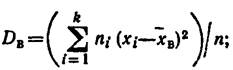
эта оценка является смещенной, так как
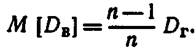
Более удобна формула
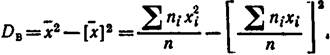
Замечание 2. Если первоначальные варианты xi – большие числа, то целесообразно вычесть из всех вариант одно и то же число С, равное выборочной средней или близкое к ней, т. е. перейти к условным вариантам ui=xi–C (дисперсия при этом не изменится).
Тогда
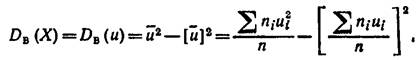
Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число С =10k, т.е. переходят к условным вариантам u i = Cx i. При этом дисперсия увеличится в С2 раз.
Поэтому, найдя дисперсию условных вариант, надо разделить ее на С2:
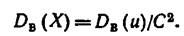
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия
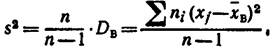
Более удобна формула
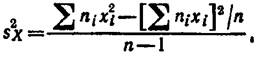
В условных вариантах она имеет вид
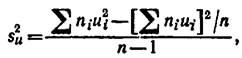
причем если u i = x i – C, то Sx2=Su2 если u i = Cx i, то Sx2=Su2/C2.
Замечание 4. При большом числе данных используют метод произведений или метод сумм.
Задача 1. Из генеральной совокупности извлечена выборка объема n=50:
| варианта
| хi
| 2
| 5
| 7
| 10
|
| частота
| n1i
| 16
| 12
| 8
| 14
|
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя
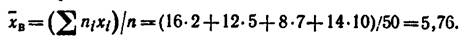
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.
Если распределение определяется одним параметром, то для его отыскания приравнивают одни теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: ν1=M1. Учитывая, что ν1=M(X) и M1= 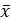 B, получим М (X)=
B, получим М (X)= 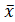 B.
B.
Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение М (X)= 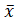 B относительно неизвестного параметра, тем самым получим его точечную оценку.
B относительно неизвестного параметра, тем самым получим его точечную оценку.
Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: ν1=M1, μ2=m2.
Учитывая, что ν 1=M(X), M1= 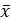 B, μ2=D(X), m2=DB, имеем
B, μ2=D(X), m2=DB, имеем
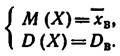
Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив данную систему относительно неизвестных параметров, тем самым получим их точечные оценки.
Для вычисления выборочной средней 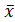 B и выборочной дисперсии DB надо располагать выборкой x 1, x 2,..., xn.
B и выборочной дисперсии DB надо располагать выборкой x 1, x 2,..., xn.
Задача 2. Случайная величина X распределена по закону Пуассона
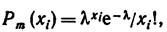
где m – число испытаний, произведенных в одном опыте; хi – число появлений события в i-м опыте.
Найти методом моментов по выборке x1, x2,..., xn точечную оценку неизвестного параметра ʎ, определяющего распределение Пуассона.
Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравняем начальный теоретический момент первого порядка ν1 начальному эмпирическому моменту первого порядка М1: ν1= М1
Приняв во внимание, что ν1=М(Х), M1= 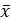 B, получим M(X)=
B, получим M(X)= 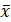 B. Учитывая, что математическое ожидание распределения Пуассона равно параметру ʎ этого распределения, окончательно имеем ʎ =
B. Учитывая, что математическое ожидание распределения Пуассона равно параметру ʎ этого распределения, окончательно имеем ʎ = 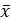 B.
B.
Итак, точечной оценкой параметра к распределения Пуассона служит выборочная средняя: ʎ *= 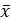 B.
B.
Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью γ покрывает заданный параметр.
1. Интервальной оценкой (с надежностью γ) математического ожидания а нормально распределенного количественного признака X по выборочной средней 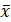 B при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал:
B при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал:
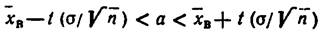
где t (σ / 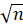 )=δ – точность оценки, n – объем выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф (t) = γ /2; при неизвестном σ (и объеме выборки л < 30)
)=δ – точность оценки, n – объем выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф (t) = γ /2; при неизвестном σ (и объеме выборки л < 30) 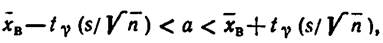 где s – «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ.
где s – «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ.
2. Интервальной оценкой (с надежностью γ) среднего квадратического отклонения нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит доверительный интервал
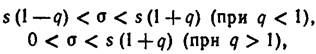
где q находят по таблице по заданным n и γ.
3. Интервальной оценкой (с надежностью γ) неизвестной вероятности р биномиального распределения по относительной частоте ω служит доверительный интервал (с приближенными концами p1 и р2)
p1 < р< р2
где

где n – общее число испытаний; m – число появлений события; ω – относительная частота, равная отношению m/n; t — значение аргумента функции Лапласа, при котором Ф(t) =γ/2 (γ —заданная надежность).
Замечание. При больших значениях n (порядка сотен) можно принять в качестве приближенных границ доверительного интервала
Задача 3. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной совокупности, если генеральное среднее квадратическое отклонение σ =5, выборочная средняя 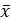 B=14 и объем выборки n=25.
B=14 и объем выборки n=25.
Решение. Требуется найти доверительный интервал
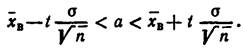
Все величины, кроме t, известны. Найдем t из соотношения Ф(t) = 0,95/2 = 0,475. По таблице находим t = 1,96.
Подставив t=1,96, 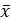 B=14, σ =5, n=25 в приведенную выше формулу, окончательно получим искомый доверительный интервал 12,04 < а < 15,96.
B=14, σ =5, n=25 в приведенную выше формулу, окончательно получим искомый доверительный интервал 12,04 < а < 15,96.
Оборудование
Персональный компьютер с установленной операционной системой Windows XP/7/8, браузер (Например, Internet Explorer, Google Chrome, Opera), текстовый редактор OOo Writer (MS Word), пакет офисных приложений «Мой офис».
Оборудование
Персональный компьютер с установленной операционной системой Windows XP/7/8, браузер (Например, Internet Explorer, Google Chrome, Opera), текстовый редактор OOo Writer (MS Word), пакет офисных приложений «Мой офис».
Задание на работу
Вариант 1
1. По выборке объема n=51 найдена смещенная оценка DB=5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
2. Случайная величина X (число семян сорняков в пробе зерна) распределена по закону Пуассона. Ниже приведено распределение семян сорняков в n=1000 пробах зерна (в первой строке указано количество xi сорняков в одной пробе; во второй строке указана частота ni – число проб, содержащих xi семян сорняков):
| xi
| 0
| 1
| 2
| 3
| 4
| 5
| 6
|
| ni
| 405
| 366
| 175
| 40
| 8
| 4
| 2
|
Найти методом моментов точечную оценку неизвестного параметра распределения Пуассона.
3. Произведено 10 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем «исправленное» среднее квадратическое отклонение s случайных ошибок измерений оказалось равным 0,8. Найти точность прибора с надежностью 0,95. Предполагается, что результаты измерений распределены нормально.
Вариант 2
1. В итоге четырех измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 8; 9; 11; 12. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсии ошибок прибора.
2. Случайная величина X (число нестандартных изделий в партии изделий) распределена по закону Пуассона. Ниже приведено распределение нестандартных изделий в n=200 партиях (в первой строке указано количество хi нестандартных изделий в одной партии; во второй строке указана частота ni – число партий, содержащих хi, нестандартных изделий):
| хi
| 0
| 1
| 2
| 3
| 4
|
| ni
| 132
| 43
| 20
| 3
| 2
|
Найти методом моментов точечную оценку неизвестного параметра ʎ, распределения Пуассона.
3. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений σ=40 м произведено пять равноточных измерений расстояния от орудия до цели. Найти доверительный интервал для оценки истинного расстояния а до цели с надежностью γ=0,95, зная среднее арифметическое результатов измерений  в=2000 м. Предполагается, что результаты измерений распределены нормально.
в=2000 м. Предполагается, что результаты измерений распределены нормально.
Вариант 3
1. Найти выборочную дисперсию по данному распределению выборки объема n=100:
| хi
| 340
| 360
| 375
| 380
|
| ni
| 20
| 50
| 18
| 12
|
Указание. Перейти к условным вариантам ui=xi–360.
2. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы σ=40ч. Предполагается, что продолжительность горения ламп распределена нормально.
3. Производятся независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,99, если в 100 испытаниях событие А появилось 60 раз.
Вариант 4
1. Найти выборочную дисперсию по данному распределению выборки объема n=50:
| хi
| 0,1
| 0,5
| 0,6
| 0,8
|
| ni
| 5
| 15
| 20
| 10
|
Указание. Перейти к условным вариантам ui=10xi.
2. Случайная величина X (время работы элемента) имеет показательное распределение  (x≥0). Ниже приведено эмпирическое распределение среднего времени работы n=200 элементов (в первой строке приведено среднее время хi работы элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем хi, часов):
(x≥0). Ниже приведено эмпирическое распределение среднего времени работы n=200 элементов (в первой строке приведено среднее время хi работы элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем хi, часов):
| хi
| 2,5
| 7,5
| 12,5
| 17,5
| 22,5
| 27,5
|
| ni
| 133
| 45
| 15
| 4
| 2
| 1
|
Найти методом моментов точечную оценку неизвестного параметра показательного распределения.
3. Из генеральной совокупности извлечена выборка объема n=12:
| хi
| -0,5
| -0,4
| -0,2
| 0
| 0,2
| 0,6
| 0,8
| 1
| 1,2
| 1,5
|
| ni
| 1
| 2
| 1
| 1
| 1
| 1
| 1
| 1
| 2
| 1
|
Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
Вариант 5
1. Найти выборочную дисперсию по данному распределению выборки объема n=50:
| хi
| 18,4
| 18,9
| 19,3
| 19,6
|
| ni
| 5
| 10
| 20
| 15
|
Указание. Перейти к условным вариантам ui=10xi –195.
2. Найти методом моментов оценку параметра р геометрического распределения 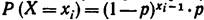 , если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
, если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
3. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределенной генеральной совокупности по выборочной средней равна 0,2, если известно среднее квадратическое отклонение генеральной совокупности σ=1,5.
Вариант 6
1. 1. По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений  в=42,8 и «исправленное» среднее квадратическое отклонение s=8. Оценить истинное значение измеряемой величины с надежностью γ=0,999.
в=42,8 и «исправленное» среднее квадратическое отклонение s=8. Оценить истинное значение измеряемой величины с надежностью γ=0,999.
2. Станок-автомат штампует валики. По выборке объема n=100 вычислена выборочная средняя диаметров изготовленных валиков. Найти с надежностью 0,95 точность δ, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение σ=2 мм. Предполагается, что диаметры валиков распределены нормально.
3. Найти методом моментов по выборке х1, х2,.... хn точечную оценку неизвестного параметра ʎ показательного распределения, плотность которого 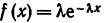 (x≥0).
(x≥0).
Вариант 7
1. Произведено 300 испытаний, в каждом из которых неизвестная вероятность р появления события А постоянна. Событие А появилось в 250 испытаниях. Найти доверительный интервал, покрывающий неизвестную вероятность р с надежностью 0,95.
2. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания а нормально распределенного признака X генеральной совокупности, если известны генеральное среднее квадратическое отклонение σ, выборочная средняя  в и объем выборки: а) σ=4,
в и объем выборки: а) σ=4,  в=10,2, n=16; б) σ= 5,
в=10,2, n=16; б) σ= 5,  в=16,8, n=25.
в=16,8, n=25.
3. Из генеральной совокупности извлечена выборка объема n=50:
| xi
| 2
| 5
| 7
| 10
|
| ni
| 16
| 12
| 8
| 14
|
Найти несмещенную оценку генеральной средней.
Вариант 8
1. По выборке объема n=51 найдена смещенная оценка DB=5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
2. В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены следующие результаты (в мм): 92; 94; 103; 105; 106. Найти: а) выборочную среднюю длину стержня; б) выборочную и исправленную дисперсии ошибок прибора.
3. Ниже приведены результаты измерения роста (в см) случайно отобранных 100 студентов.
| Рост
| 154-I58
| l58-162
| 162-166
| 166-170
| 170-174
| 174-178
| 178-182
|
| Число студентов
| 10
| 14
| 26
| 28
| 12
| 8
| 2
|
Найти выборочную среднюю и выборочную дисперсию роста обследованных студентов.
Вариант 9
1. В итоге четырех измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 8; 9; 11; 12. Найти: а) выборочную среднюю результатов измерений; б) выборочную и исправленную дисперсии ошибок прибора.
2. Из генеральной совокупности извлечена выборка объема n=60:
Найти несмещенную оценку генеральной средней.
3. Найти методом моментов оценку параметра р геометрического распределения Р(Х=хi)=(1–р)xi-1 если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
Вариант 10
1. Найти выборочную дисперсию по данному распределению выборки объема n=100:
| Хi
| 340
| 360
| 375
| 380
|
| ni
| 20
| 50
| 18
| 12
|
2. Найти методом моментов по выборке x1, x2..., xn точечные оценки неизвестных параметров α и σ нормального распределения, плотность которого: 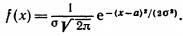
3. Случайная величина X (ошибка измерения даль ности радиодальномером) подчинена равномерному за кону распределения с неизвестными параметрами а и b. Ниже приведено эмпирическое распределение средней ошибки n=200 измерений дальности (в первой строке указана средняя ошибка xi; во второй строке указана частота ni –количество измерений, имеющих среднюю ошибку xi):
| xi
| 3
| 5
| 7
| 9
| 11
| 13
| 15
| 17
| 19
| 21
|
| ni
| 21
| 16
| 15
| 26
| 22
| 14
| 21
| 22
| 18
| 25
|
Найти методом моментов точечные оценки неизвестных параметров а и b равномерного распределения.
7. Контрольные вопросы
1. Что такое точечная статистическая оценка?
2. Что является статистической оценкой математического ожидания?
3. Что является статистической оценкой дисперсии?
4. Что является статистической оценкой среднего квадратического отклонения?
5. Несмещённость, состоятельность, эффективность статистических оценок.
6. Почему вычисляется исправленная дисперсия и исправленное среднее квадратическое отклонение?
7. Что меньше: выборочная дисперсия или несмещённая дисперсия?
Практическая работа №3
Цель и задачи работы
Целью практической работы является практическое применение статистических критериев: для решения каких задач они используются, при анализе каких выборок – зависимых или независимых, больших или малых, с известным распределением или неизвестным, при исследовании признаков, выраженных в различных шкалах измерения.
Порядок выполнения работы
- ознакомится с теоретическими сведениями;
- выполнить задание;
- оформить отчет;
- ответить на контрольные вопросы, заданные преподавателем.
Оформление отчета
Отчет должен содержать: титульный лист, цель работы, описание пунктов выполнения лабораторной работы в соответствии с заданием, ответы на контрольные вопросы и выводы по работе.
Теоретические сведения
Методы математической статистики широко используются при анализе различных процессов и явлений. Если по результатам проведённых экспериментов требуется проверить некоторое предположение относительно генеральной совокупности и сделать обоснованный вывод, то используется статистическая проверка гипотез. Например, если сравниваются различные способы лечения, или разные варианты инвестиций, измерений, технологических процессов, рассматриваются вопросы об эффективности нового метода обучения, управления, о значимости математической модели и т.д. Практической реализации эксперимента предшествует этап, на котором исследователь должен чётко сформулировать предположение, подлежащее проверке.
Предположительное утверждение относительно генеральной совокупности, проверяемое по выборочным данным, называется статистической гипотезой. Далее осуществляется проверка фактического соответствия реальных результатов экспериментов предполагаемой гипотезе. Различают простую и сложную статистические гипотезы.
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения случайной величины. Например, гипотезы «вероятность появления события в схеме Бернулли равна 1/2», «закон распределения случайной величины – нормальный с параметрами a=0, σ=1» – являются простыми, а гипотезы «вероятность появления события в схеме Бернулли заключена между 0,3 и 0,6», «закон распределения не является нормальным» – сложными.
Проверяемую гипотезу обычно называют нулевой или основной и обозначают H0. Наряду с нулевой гипотезой H0 рассматривают альтернативную, или конкурирующую, гипотезу H1, являющуюся логическим отрицанием H0. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез. Например, для простой нулевой гипотезы H0: p = 1/ 2 сложная альтернативная гипотеза может выглядеть таким образом H1: p ¹ 1/ 2 или так H1: p < 1/ 2 или H1: p > 1/ 2.
Правило, по которому принимается решение об отклонении или принятии основной гипотезы H0, называется критерием. Суть проверки статистической гипотезы заключается в том, что все выборочное пространство делится на две взаимодополняющие области: критическую область Sкр (область неправдоподобно малых и/или неправдоподобно больших значений) и область допустимых значений Sкр (область правдоподобных значений). В зависимости от вида альтернативной гипотезы H1 различают односторонние (критическая область с одной стороны) и двухсторонние критерии (критических области две – «два хвоста распределения»). Затем по выборке x1….xn определяется специально составленная выборочная характеристика – критическая статистика θкр (x1, x2,...,xn), точное или приближенное распределение которой известно. Для этого известного распределения по специальным таблицам находятся точки θкр.н и θкр.в (в случае двухсторонней критической области) или точка θкр (в случае односторонней критической области), разделяющие критическую область Sкр и область допустимых значений Sкр. Для одностороннего критерия область принятия основной гипотезы имеет ограничение только с одной стороны (сверху или снизу), соответственно требуется найти квантиль уровня 1- α, либо квантиль уровня α. Для двухстороннего критерия область принятия нулевой гипотезы имеет два ограничения – сверху (квантиль уровня 1-α/2) и снизу (квантиль уровня α / 2). Рассчитывается эмпирическое значение статистики θэмп подстановкой в θкр конкретных выборочных значений. Если θэмп Î Sкр, то нулевая гипотеза отклоняется и принимается альтернативная гипотеза. Если же θэмп Î Sкр, то делается вывод о том, что нет оснований для отклонения нулевой гипотезы.
Так как исследователь работает с выборочными данными, которые попадают из генеральной совокупности случайным образом, то можно совершить ошибки (табл.1).

Если на самом деле верной является нулевая гипотеза, а будет принята альтернативная гипотеза, то такая ошибка называется ошибкой первого рода. Вероятность P(H1/H0)=α допустить ошибку 1-го рода называется уровнем значимости критерия.
Ошибка второго рода – это принятие нулевой гипотезы в то время, когда на самом деле верной является альтернативная гипотеза. Вероятность допустить ошибку 2-го рода: P(H0 / H1) = β.
При построении процедур проверки гипотез желательно минимизировать значения ошибок обоих родов, но на практике это невозможно: при фиксированном объёме выборки можно минимизировать лишь одну из величин α или β, другая при этом будет увеличиваться. Поэтому поступают таким образом: фиксируют 6 вероятность ошибки первого рода на определённом уровне (обычно для α используют стандартные значения, например, равные 0,05; 0,01), а вероятность ошибки второго рода – минимизируют.
Мощностью критерия называется вероятность не допустить ошибку



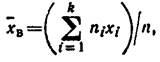
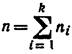 – объем выборки.
– объем выборки.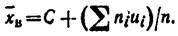
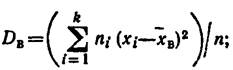
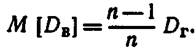
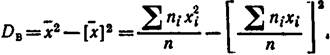
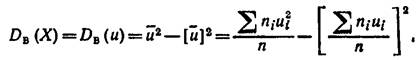
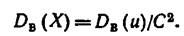
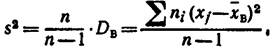
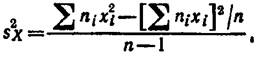
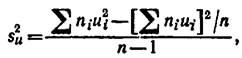
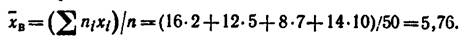
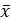 B, получим М (X)=
B, получим М (X)= 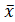 B.
B.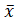 B относительно неизвестного параметра, тем самым получим его точечную оценку.
B относительно неизвестного параметра, тем самым получим его точечную оценку.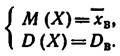
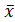 B и выборочной дисперсии DB надо располагать выборкой x 1, x 2,..., xn.
B и выборочной дисперсии DB надо располагать выборкой x 1, x 2,..., xn.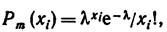
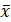 B. Учитывая, что математическое ожидание распределения Пуассона равно параметру ʎ этого распределения, окончательно имеем ʎ =
B. Учитывая, что математическое ожидание распределения Пуассона равно параметру ʎ этого распределения, окончательно имеем ʎ = 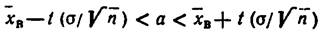
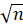 )=δ – точность оценки, n – объем выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф (t) = γ /2; при неизвестном σ (и объеме выборки л < 30)
)=δ – точность оценки, n – объем выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф (t) = γ /2; при неизвестном σ (и объеме выборки л < 30) 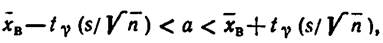 где s – «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ.
где s – «исправленное» выборочное среднее квадратическое отклонение, tγ находят по таблице по заданным n и γ.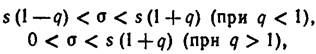

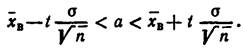
 в=2000 м. Предполагается, что результаты измерений распределены нормально.
в=2000 м. Предполагается, что результаты измерений распределены нормально. (x≥0). Ниже приведено эмпирическое распределение среднего времени работы n=200 элементов (в первой строке приведено среднее время хi работы элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем хi, часов):
(x≥0). Ниже приведено эмпирическое распределение среднего времени работы n=200 элементов (в первой строке приведено среднее время хi работы элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем хi, часов):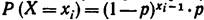 , если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.
, если в четырех опытах событие появилось соответственно после двух, четырех, шести и восьми испытаний.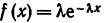 (x≥0).
(x≥0).