Решить задачу нестационарной теплопроводности это значит найти зависимость изменения температуры и количество теплоты переданной телу во времени для любой точки тела:
t = f (x; y; z; τ) и Q = φ (x; y; z; τ).
Для аналитического нахождения этих зависимостей может быть использовано дифференциальное уравнение теплопроводности Фурье:
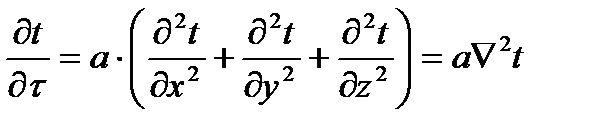 .
.
Это уравнение решается с помощью рядов Фурье. Аналитическое решение получается очень сложным и возможно лишь для тел простой формы (пластины, цилиндра и шара) при целом ряде упрощающих предпосылок.
Аналитическое описание процесса теплопроводности кроме дифференциального уравнения также включает в себя и условия однозначности.
Условия однозначности задаются в виде:
· физических параметров 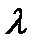 ,
,  ,
,  ;
;
· формы и геометрических размеров объекта 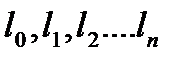 ;
;
· температуры тела в начальный момент времени 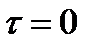 ; t = t0 = f(x, у, z).
; t = t0 = f(x, у, z).
· граничных условий, которые могут быть заданы в виде граничных условий третьего рода:
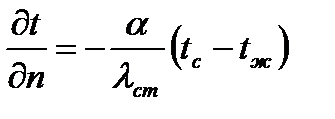 .
.
Дифференциальное уравнение теплопроводности совместно с условиями однозначности дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции, которая удовлетворяла бы уравнению и условиям однозначности.
t=f(x,y,z,i,a,t0,tж, 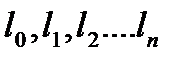 )
)
Если решить это уравнение для плоской стенки и рассмотреть процесс изменения температуры только в одном направлении x, то решение будет иметь следующий вид:
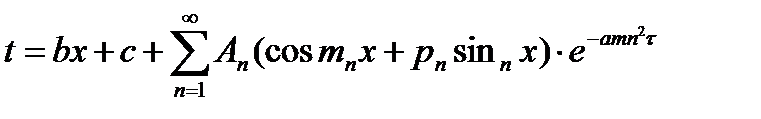 ,
,
где b и c определяются из условий стационарности процесса, т.е. при 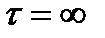 ;
;
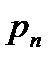 ,
, 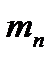 - из граничных условий 3 рода;
- из граничных условий 3 рода;
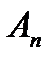 - из начальных условий, т.е. при
- из начальных условий, т.е. при 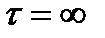 .
.
Из уравнения видно, что искомая функция t зависит от большого числа переменных, которые можно сгруппировать в 3 безразмерных комплекса, эти комплексы называются числами подобия.
Первое число подобия - Число Био:
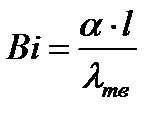 ,
,
где 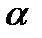 - коэффициент теплоотдачи на границе жидкости и твердого тела;
- коэффициент теплоотдачи на границе жидкости и твердого тела;
λ - коэффициент теплопроводности твердого тела;
l - характеристический размер, который определяется в зависимости от формы тела:
для пластины l =δ;
для цилиндра l =  ;
;
для шара l =  .
.
Второе число подобия - Число Фурье:
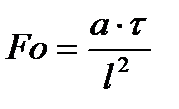 ,
,
где a - коэффициент температуропроводности;
τ – время.
Число Фурье называют также безразмерным временем.
Третий безразмерный комплекс - безразмерная координата:
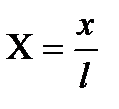 .
.
Установлено, что θ - безразмерная температура, является функцией чисел Био и Фурье, для фиксированных значений  , т.е.
, т.е.
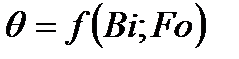
.
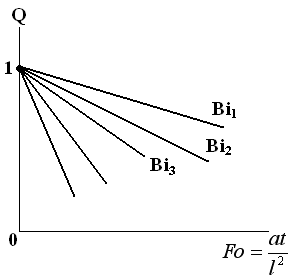
Изменение безразмерной температуры θ для центра ( 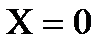 ) и поверхности (
) и поверхности (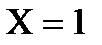 ) можно представить графическим решением, которое приведено на рисунке 1.6.3.
) можно представить графическим решением, которое приведено на рисунке 1.6.3.
Подобные графики построены для центра и поверхности пластины, цилиндра и шара, а так же для безразмерного количества теплоты, которая является функцией числа Bi и  :
:
 .
.
Следовательно, чтобы определить температуру на поверхности или в центре тела необходимо знать две величины: число Bi и число  .
.
Таким образом, метод решения задач нестационарной теплопроводности заключается в следующем:
1) задаются геометрическими, начальными и граничными условиями [(с;λ; 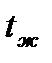 ;
;  ;α;
;α; 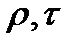 ),(
),( или
или 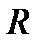 )];
)];
2) вычисляют числа Bi и  ;
;
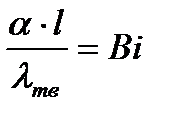 ,
, 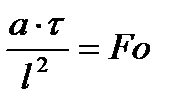 ;
;
3) зная числа Bi и  по графику, определяют безразмерную температуру θ;
по графику, определяют безразмерную температуру θ;
4) определив θ, рассчитывают температуру в центре

или на поверхности тела
 ,
,
где 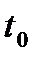 - начальная температура тела;
- начальная температура тела;
 - температура среды.
- температура среды.
Рассмотрим влияние значений чисел Bi на распределение температуры в теле на примере охлаждения пластины.
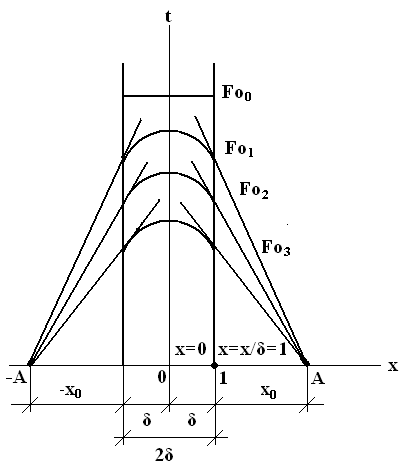
Из полученного решения следует, что для любого момента времени температурное поле имеет вид симметричной кривой с максимумом на оси пластины
( 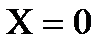
). В каждый последующий момент будет своя кривая, монотонно убывающая к поверхности (рис. 1.6.4).
Для любого момента времени касательные к кривым в точках 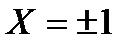 проходят через направляющие точки +А и
проходят через направляющие точки +А и
– А, которые расположены на расстоянии 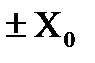 от поверхности пластины, причем
от поверхности пластины, причем
 или
или  ,
,
отсюда 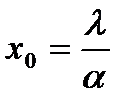 , т.е. расстояние до точки А полностью определяется условиями однозначности.
, т.е. расстояние до точки А полностью определяется условиями однозначности.
Сказанное справедливо для всех поверхностей.



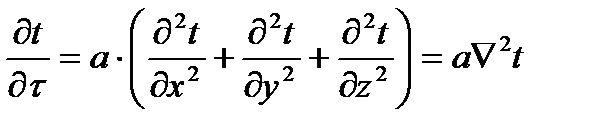 .
. 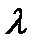 ,
,  ,
,  ;
;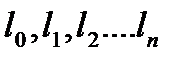 ;
;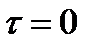 ; t = t0 = f(x, у, z).
; t = t0 = f(x, у, z).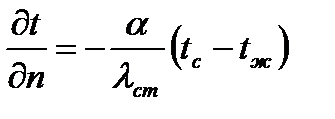 .
. 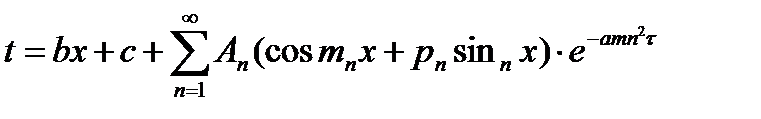 ,
, 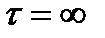 ;
;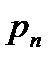 ,
, 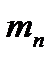 - из граничных условий 3 рода;
- из граничных условий 3 рода;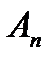 - из начальных условий, т.е. при
- из начальных условий, т.е. при 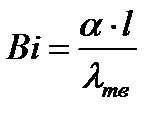 ,
,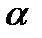 - коэффициент теплоотдачи на границе жидкости и твердого тела;
- коэффициент теплоотдачи на границе жидкости и твердого тела; ;
; .
.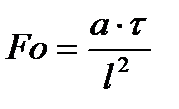 ,
, 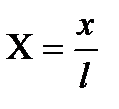 .
. , т.е.
, т.е.
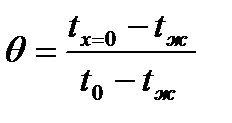
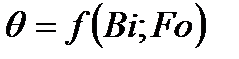 .
.
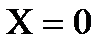 ) и поверхности (
) и поверхности (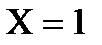 ) можно представить графическим решением, которое приведено на рисунке 1.6.3.
) можно представить графическим решением, которое приведено на рисунке 1.6.3. :
: .
.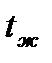 ;
;  ;α;
;α; 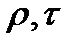 ),(
),( или
или 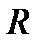 )];
)]; ;
;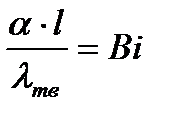 ,
, 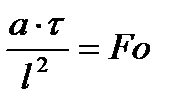 ;
; по графику, определяют безразмерную температуру θ;
по графику, определяют безразмерную температуру θ;
 ,
,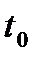 - начальная температура тела;
- начальная температура тела; - температура среды.
- температура среды.
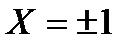 проходят через направляющие точки +А и
проходят через направляющие точки +А и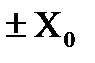 от поверхности пластины, причем
от поверхности пластины, причем или
или  ,
,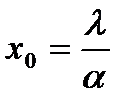 , т.е. расстояние до точки А полностью определяется условиями однозначности.
, т.е. расстояние до точки А полностью определяется условиями однозначности.

