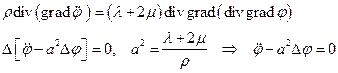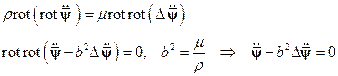Модель линейно вязкой жидкости
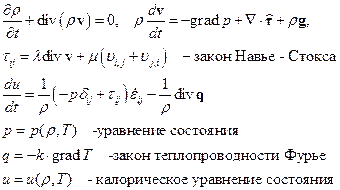
Уравнение движения Навье – Стокса – Дюгема:
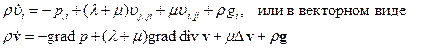
Для несжимаемой жидкости – уравнение Навье – Стокса
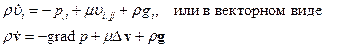 (1)
(1)
Для несжимаемой жидкости уравнения (1) вместе с уравнением неразрывности
 (2)
(2)
образуют замкнутую систему уравнений (1), (2). В качестве граничных условий на границе тела принимаются условия прилипания (скорость жидкости совпадает со скоростью точки границы).
Ламинарное течение. Течение Пуазейля
Практика показала, что уравнения Навье – Стокса достаточно хорошо описывают течения реальной жидкости в случае умеренных скоростей потока. Такие течения принято называть ламинарными (слоистыми). В тоже время, при возрастании скорости наступает хаотизация поля скоростей с активацией перемешивания – поток становится турбулентным.
Одним из примеров ламинарного течения вязкой жидкости является стационарное течение вязкой жидкости в трубе, т.н. течение Пуазейля.
Рассмотрим стационарное (установившееся) течение вязкой несжимаемой однородной жидкости в круглой трубе с радиусом  . Запишем систему уравнений и граничных условий данной задачи, направив ось
. Запишем систему уравнений и граничных условий данной задачи, направив ось  вдоль оси симметрии трубы. Предположения о стационарности течения и однородности жидкости означают, что
вдоль оси симметрии трубы. Предположения о стационарности течения и однородности жидкости означают, что
 .
.
Граничные условия прилипания на стенках трубы: 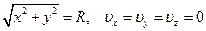 . При данных граничных условиях на стенках трубы и заданном расходе жидкости надо решить следующую систему уравнений
. При данных граничных условиях на стенках трубы и заданном расходе жидкости надо решить следующую систему уравнений
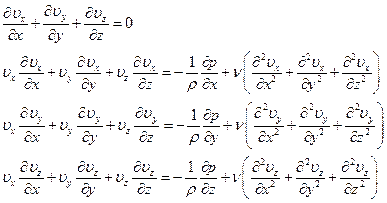
Будем искать поле скоростей в следующей форме:
 .
.
Отметим, что уравнение неразрывности будет выполнено тожественно. Из первого и второго уравнений движения будет следовать, что давление будет функцией осевой координаты 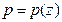
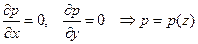 .
.
Проекция третьего уравнения движения примет следующую форму
 .
.
Это равенство возможно, если величина  является постоянной. Обозначим её как
является постоянной. Обозначим её как 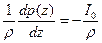 , где
, где  – перепад давления на единицу длины трубы. Учитывая значения производных
– перепад давления на единицу длины трубы. Учитывая значения производных

получим обыкновенное дифференциальное уравнение для скорости 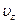 с нулевым условием на стенке трубы
с нулевым условием на стенке трубы
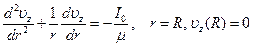 .
.
Решим уравнение
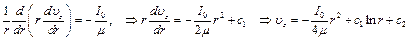
Из условия ограниченности скорости следует, что константа  , а вторая константа определяется из граничного условия
, а вторая константа определяется из граничного условия
 .
.
Оставшаяся величина  определяется заданным расходом жидкости
определяется заданным расходом жидкости 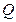

Можно определить плотность вязких сил, действующих на единицу длины трубы.

Пограничный слой. Турбулентность.
При увеличении скорости в рамках задачи Пуазейля, начиная с некоторого критического значения этой скорости, ламинарное слоистое течение сменится турбулентным течением. Если в поток добавить окрашенную струйку жидкости, то при ламинарном течении она будет оставаться локализованной около рассматриваемой линии тока. В турбулентном режиме вся жидкость в трубе окрасится. Слоистое течение сменится т.н. турбулентным потоком. Для задачи Пуазейля это означает, что появятся ненулевые составляющие у тех компонент скорости, которые в рамках ламинарного течения были равны нулю.
В стационарных течениях инерционные силы характеризуются величиной
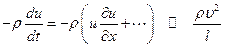 .
.
Вязкие силы характеризуются величиной
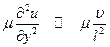 .
.
Отношение этих сил будет безразмерным числом, которое называется числом Рейнольдса в честь английского учёного Осборна Рейнольдса
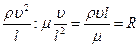 .
.
При экспериментальном моделировании обтекания тел мы должны обеспечить не только геометрическое подобие тел, но и равенство чисел Рейнольдса. Если преобладают силы вязкости, можно пренебречь силами инерции. Этот случай часто называют приближением Стокса. Например, сила сопротивления движению шара радиусом 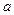 в приближении Стокса равна
в приближении Стокса равна  . Эта формула справедлива лишь при малых числах Рейнольдса
. Эта формула справедлива лишь при малых числах Рейнольдса 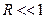 . Наоборот, при движении с очень большими числами Рейнольдса влияние вязких сил на течение ничтожно мало практически во всей области течения, за исключением тонкого слоя жидкости вблизи границы обтекаемого тела. Именно поэтому эта область течения называется пограничным слоем. В пограничном слое скорость на границе обтекаемого тела равна нулю, а на малом расстоянии от границы она фактически совпадает со скоростью обтекания, получаемой в рамках идеальной жидкости. В пограничном слое вязкие силы должны быть равными силам инерции. Если ввести толщину пограничного слоя
. Наоборот, при движении с очень большими числами Рейнольдса влияние вязких сил на течение ничтожно мало практически во всей области течения, за исключением тонкого слоя жидкости вблизи границы обтекаемого тела. Именно поэтому эта область течения называется пограничным слоем. В пограничном слое скорость на границе обтекаемого тела равна нулю, а на малом расстоянии от границы она фактически совпадает со скоростью обтекания, получаемой в рамках идеальной жидкости. В пограничном слое вязкие силы должны быть равными силам инерции. Если ввести толщину пограничного слоя 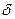 , то получим
, то получим
 .
.
Отсюда можно получить оценку для силы вязкого сопротивления, поскольку касательное напряжение оценивается величиной
 .
.
В плоском случае, оставляя слагаемые одного порядка (число Рейнольдса 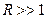 ), система уравнений потока при обтекании тела малой кривизны имеет вид
), система уравнений потока при обтекании тела малой кривизны имеет вид
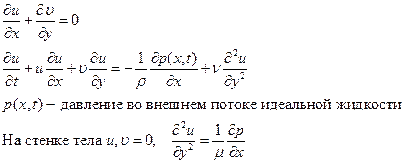
В турбулентном потоке величины получают случайные малые возмущения. Рейнольдс предложил метод осреднения уравнений Навье – Стокса. Осреднение может проводиться по времени или по пространству, но оно должно удовлетворять условиям Рейнольдса
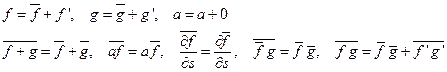
В результате осреднения уравнений Навье – Стокса получим
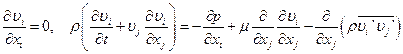
Уравнения Рейнольдса не замкнуты. Необходимо дополнительно определить тензор турбулентных (Рейнольдсовых) напряжений
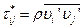 .
.
Модель линейного упругого тел, закон Гука, постановки задач теории упругости в перемещениях и напряжениях. Продольные и поперечные волны в изотропной упругой среде. Функция напряжений плоского напряженного состояния. Задача Ламе о толстостенной трубе.
Модель линейно упругой среды:
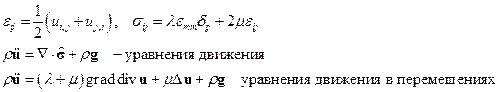
Постановка задач. На границе упругого тела задан вектор напряжений. Задача в напряжениях: 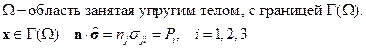
На границе упругого тела задан вектор перемещений – задача в перемещениях
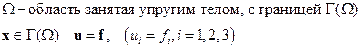
Плоская статическая задача теории упругости. Функция напряжений.
Рассмотрим два случая напряжённого состояния.
1.Случай плоско-деформированного состояния, когда 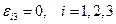 (это состояние реализуется при плоскопараллельном движении среды).
(это состояние реализуется при плоскопараллельном движении среды).
В этом случае из закона Гука следует, что отличными от нуля напряжениями будут  .
.
Закон Гука может быть переписан в форме
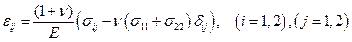 . (1)
. (1)
2.Случай плосконапряжённого состояния, когда 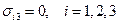 (это состояние приближённо реализуется для тонких пластин).
(это состояние приближённо реализуется для тонких пластин).
Закон Гука может быть переписан в форме
 . (2)
. (2)
В плоском случае уравнения равновесия имеют вид
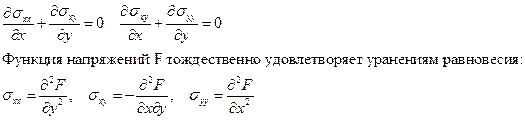
Для получения уравнения воспользуемся условиями совместности деформаций. В плосконапряженном случае получим
 .
.
В результате подстановки деформаций и напряжений получим для функции напряжений
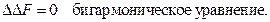
Волны в упругой среде.
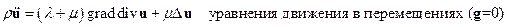
Разложим векторное поле перемещений в форме Ламе 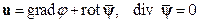 .
.
После применения операции  и операции
и операции 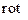 к уравнениям движения, получим
к уравнениям движения, получим
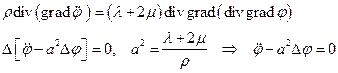
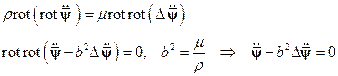



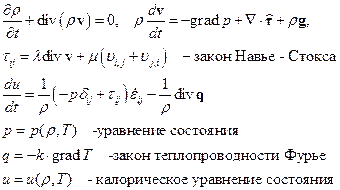
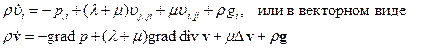
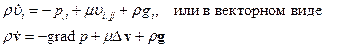 (1)
(1) (2)
(2) . Запишем систему уравнений и граничных условий данной задачи, направив ось
. Запишем систему уравнений и граничных условий данной задачи, направив ось  вдоль оси симметрии трубы. Предположения о стационарности течения и однородности жидкости означают, что
вдоль оси симметрии трубы. Предположения о стационарности течения и однородности жидкости означают, что .
.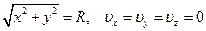 . При данных граничных условиях на стенках трубы и заданном расходе жидкости надо решить следующую систему уравнений
. При данных граничных условиях на стенках трубы и заданном расходе жидкости надо решить следующую систему уравнений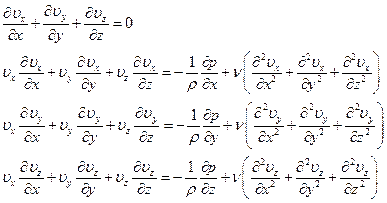
 .
.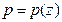
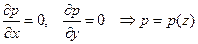 .
. .
. является постоянной. Обозначим её как
является постоянной. Обозначим её как 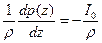 , где
, где  – перепад давления на единицу длины трубы. Учитывая значения производных
– перепад давления на единицу длины трубы. Учитывая значения производных
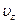 с нулевым условием на стенке трубы
с нулевым условием на стенке трубы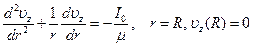 .
.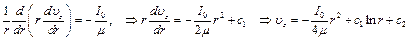
 , а вторая константа определяется из граничного условия
, а вторая константа определяется из граничного условия .
. определяется заданным расходом жидкости
определяется заданным расходом жидкости 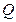


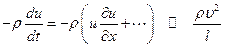 .
.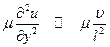 .
.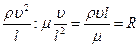 .
.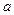 в приближении Стокса равна
в приближении Стокса равна  . Эта формула справедлива лишь при малых числах Рейнольдса
. Эта формула справедлива лишь при малых числах Рейнольдса 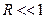 . Наоборот, при движении с очень большими числами Рейнольдса влияние вязких сил на течение ничтожно мало практически во всей области течения, за исключением тонкого слоя жидкости вблизи границы обтекаемого тела. Именно поэтому эта область течения называется пограничным слоем. В пограничном слое скорость на границе обтекаемого тела равна нулю, а на малом расстоянии от границы она фактически совпадает со скоростью обтекания, получаемой в рамках идеальной жидкости. В пограничном слое вязкие силы должны быть равными силам инерции. Если ввести толщину пограничного слоя
. Наоборот, при движении с очень большими числами Рейнольдса влияние вязких сил на течение ничтожно мало практически во всей области течения, за исключением тонкого слоя жидкости вблизи границы обтекаемого тела. Именно поэтому эта область течения называется пограничным слоем. В пограничном слое скорость на границе обтекаемого тела равна нулю, а на малом расстоянии от границы она фактически совпадает со скоростью обтекания, получаемой в рамках идеальной жидкости. В пограничном слое вязкие силы должны быть равными силам инерции. Если ввести толщину пограничного слоя 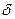 , то получим
, то получим .
. .
.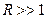 ), система уравнений потока при обтекании тела малой кривизны имеет вид
), система уравнений потока при обтекании тела малой кривизны имеет вид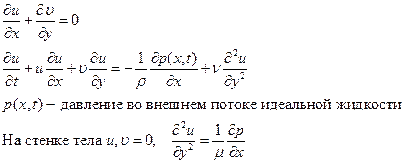
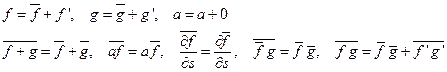
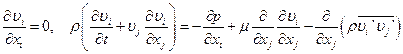
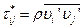 .
.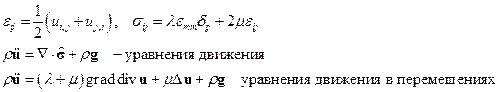
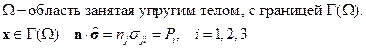
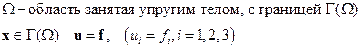
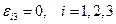 (это состояние реализуется при плоскопараллельном движении среды).
(это состояние реализуется при плоскопараллельном движении среды). .
.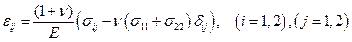 . (1)
. (1)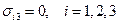 (это состояние приближённо реализуется для тонких пластин).
(это состояние приближённо реализуется для тонких пластин). . (2)
. (2)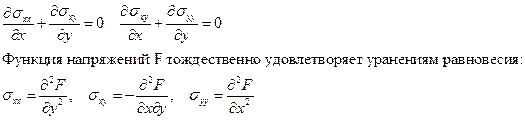
 .
.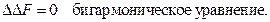
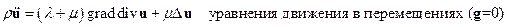
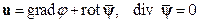 .
. и операции
и операции 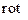 к уравнениям движения, получим
к уравнениям движения, получим