Понятие размерности физической величины тесно связано с процессом измерения, в котором физическую величину сравнивают с некоторым ее эталоном (единица измерения). Численное значение отношения измеряемой величины к величине ее эталона вместе с указанием названия эталона − размерность этой величины. В такой записи название единицы измерения можно понимать как некий алгебраический множитель иной природы, нежели числовая, и обращаться с размерными величинами по правилам алгебры с учетом этого обстоятельства.
Известно, что в системе измерения физических величин выделяется некоторое количество основных (независимых) единиц измерения, а все остальные выражаются через них. Это будут составные единицы измерения. В то же время наличие таких связей между размерностями означает, что некоторые комбинации размерных величин могут оказаться безразмерными.
Для задач термомеханики достаточно четырех основных размерностей: длины L, времени t, массы m и температуры T. Все остальные размерности выражаются через них.
Очевидно, что любая физически обоснованная зависимость размерных величин должна быть такой, чтобы ее вид не зависел от выбора системы единиц измерения. На этом принципе основана теория размерности, в которой получена П-теорема, устанавливающая условия выполнения этого принципа.
П-теорема:
связь между 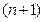 размерными величинами
размерными величинами 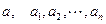 , независимая от выбора системы единиц измерения из
, независимая от выбора системы единиц измерения из 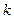 простых единиц, принимает вид соотношения между
простых единиц, принимает вид соотношения между 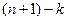 величинами
величинами 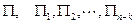 , представляющими собой безразмерные комплексы из
, представляющими собой безразмерные комплексы из 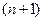 размерных величин.
размерных величин.
Т.е. функция связи  независимых размерных величин
независимых размерных величин 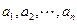 с размерной величиной
с размерной величиной 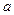 вида:
вида:
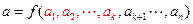 (1)
(1)
может быть представлена как связь безразмерной величины 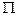 c
c  безразмерными комплексами
безразмерными комплексами 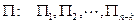 вида:
вида:
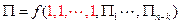 (2)
(2)
Из этой теоремы также следует, что представление физических зависимостей через безразмерные параметры позволяет сократить общее число параметров, определяющих проблему, вследствие чего упрощается исследование задачи.
При таком представлении:
а) выбирают характерные значения для всех переменных (константы обезразмеривания) и вводят безразмерные переменные как отношение их размерных величин к характерным значениям;
б) размерные константы задачи и константы обезразмеривания образуют
некоторые безразмерные комплексы (критерии), число которых значительно
меньше числа размерных констант.
При таком рассмотрении одному набору фиксированных значений критериев соответствует обширное множество наборов размерных констант, которым отвечают подобные режимы.
Таким образом, переход к т.н. безразмерным переменным имеет следующие преимущества:
1) сокращение числа независимых параметров задачи;
2) один решенный безразмерный вариант соответствует более широкому классу размерных задач;
3) все параметры задачи имеют порядок, близкий к единице, что позволяет
эффективнее использовать технологические ресурсы вычислительных машин при численном решении.
Пример 1: Математический маятник
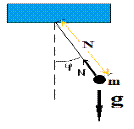
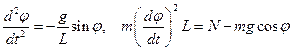

Определяющие параметры задачи 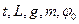
Следовательно
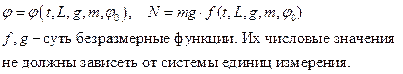
Из величин 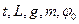 можно составить две безразмерные комбинации
можно составить две безразмерные комбинации  . Отсюда следует, что движение маятника описывается функциями вида:
. Отсюда следует, что движение маятника описывается функциями вида:
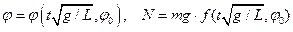 .
.
Рассмотрим период колебаний маятника. Он имеет размерность времени, поэтому
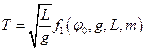
Поскольку, 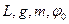 по размерности независимые величины, то отсюда следует, что
по размерности независимые величины, то отсюда следует, что
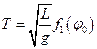
Получить саму функцию 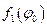 из соображений размерности нельзя. Её можно получить или теоретически, решив уравнения колебаний маятника, или экспериментально, измеряя период колебаний в зависимости от разных углов
из соображений размерности нельзя. Её можно получить или теоретически, решив уравнения колебаний маятника, или экспериментально, измеряя период колебаний в зависимости от разных углов  . Вид этой функции можно уточнить, привлекая соображения симметрии. Физически ничего не изменится, если вместо угла
. Вид этой функции можно уточнить, привлекая соображения симметрии. Физически ничего не изменится, если вместо угла 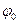 взять в качестве начального условия
взять в качестве начального условия 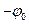 . То есть – эта функция чётная. Если предположить, что она аналитическая в нуле, то её можно разложить в ряд Тейлора
. То есть – эта функция чётная. Если предположить, что она аналитическая в нуле, то её можно разложить в ряд Тейлора
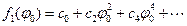 . Для малых углов, пренебрегая малыми величинами второго порядка, получим
. Для малых углов, пренебрегая малыми величинами второго порядка, получим  .
.
Пример 2: Истечение тяжелой жидкости через водослив плотины.
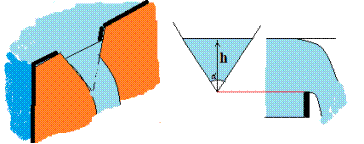
Рассмотрим расход Q, вытекающей в единицу времени через плотину жидкости, как функцию параметров задачи. В качестве параметров естественно рассмотреть плотность 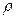 жидкости, напор
жидкости, напор 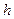 , ускорение сил тяжести g. Тогда можно искать эту функцию в виде:
, ускорение сил тяжести g. Тогда можно искать эту функцию в виде: 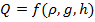 .
.
Анализ размерностей позволяет записать эту функцию в следующей форме  .
.



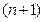 размерными величинами
размерными величинами 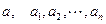 , независимая от выбора системы единиц измерения из
, независимая от выбора системы единиц измерения из 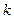 простых единиц, принимает вид соотношения между
простых единиц, принимает вид соотношения между 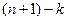 величинами
величинами 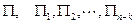 , представляющими собой безразмерные комплексы из
, представляющими собой безразмерные комплексы из 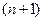 размерных величин.
размерных величин. независимых размерных величин
независимых размерных величин 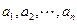 с размерной величиной
с размерной величиной 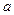 вида:
вида: 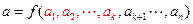 (1)
(1)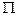 c
c  безразмерными комплексами
безразмерными комплексами 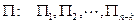 вида:
вида: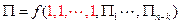 (2)
(2)
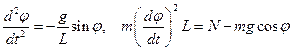

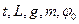
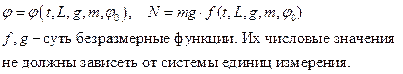
 . Отсюда следует, что движение маятника описывается функциями вида:
. Отсюда следует, что движение маятника описывается функциями вида: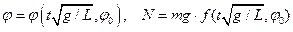 .
.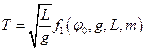
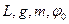 по размерности независимые величины, то отсюда следует, что
по размерности независимые величины, то отсюда следует, что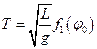
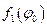 из соображений размерности нельзя. Её можно получить или теоретически, решив уравнения колебаний маятника, или экспериментально, измеряя период колебаний в зависимости от разных углов
из соображений размерности нельзя. Её можно получить или теоретически, решив уравнения колебаний маятника, или экспериментально, измеряя период колебаний в зависимости от разных углов  . Вид этой функции можно уточнить, привлекая соображения симметрии. Физически ничего не изменится, если вместо угла
. Вид этой функции можно уточнить, привлекая соображения симметрии. Физически ничего не изменится, если вместо угла 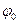 взять в качестве начального условия
взять в качестве начального условия 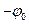 . То есть – эта функция чётная. Если предположить, что она аналитическая в нуле, то её можно разложить в ряд Тейлора
. То есть – эта функция чётная. Если предположить, что она аналитическая в нуле, то её можно разложить в ряд Тейлора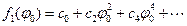 . Для малых углов, пренебрегая малыми величинами второго порядка, получим
. Для малых углов, пренебрегая малыми величинами второго порядка, получим  .
.
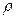 жидкости, напор
жидкости, напор 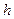 , ускорение сил тяжести g. Тогда можно искать эту функцию в виде:
, ускорение сил тяжести g. Тогда можно искать эту функцию в виде: 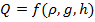 .
. .
.

