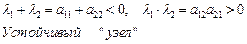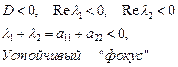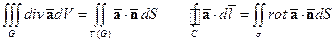Фундаментальная система решений системы линейных дифференциальных уравнений с постоянными коэффициентами. Метод вариации постоянных. Классификация Пуанкаре особых точек на плоскости. Решение линейного уравнение n-го порядка, квази-многочлены.

Нормальная система уравнений с постоянными коэффициентами
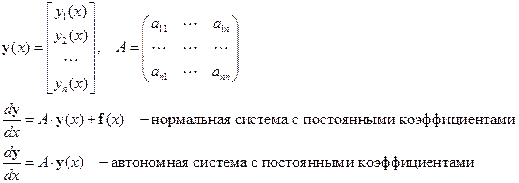
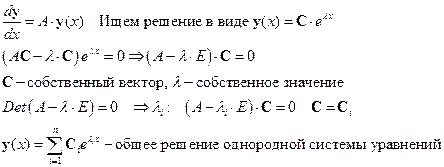
Примеры:
1.Решить систему уравнений
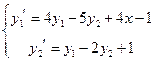
Найти решение с начальными условиями 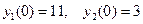 .
.
Ответ: 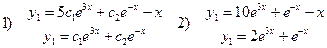
2.Найти общее решение уравнения

Ответ: 
3.Исследовать особые точки автономных систем уравнений.

а) 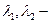 действительные, отрицательные числа (устойчивый узел).
действительные, отрицательные числа (устойчивый узел).
Устойчивый режим узлового типа. Система совершает апериодически затухающее движение, приближаясь к положению равновесия.
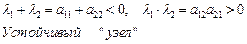
б) 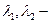 действительные положительные числа (неустойчивый узел). Неустойчивый режим узлового типа. Система удаляется от положения равновесия.
действительные положительные числа (неустойчивый узел). Неустойчивый режим узлового типа. Система удаляется от положения равновесия.

в) 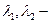 комплексные числа с отрицательной действительной частью (устойчивый фокус). Устойчивый режим фокального типа. Система совершает периодические затухающие колебания и асимптотически приближается к положению равновесия.
комплексные числа с отрицательной действительной частью (устойчивый фокус). Устойчивый режим фокального типа. Система совершает периодические затухающие колебания и асимптотически приближается к положению равновесия.
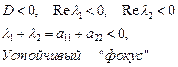
г) 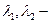 комплексные числа с положительной действительной частью (неустойчивый фокус). Неустойчивый режим фокального типа. Этот тип движения соответствует периодическим колебаниям с нарастающей амплитудой. В таком случае говорят о режиме самовозбуждающихся колебаний. В реальных системах нарастание амплитуды обычно ограничено физическими процессами, так что возникает устойчивое периодическое движение с постоянной во времени амплитудой. Фазовая траектория при этом накручивается на предельный цикл, соответствующий устойчивым автоколебаниям.
комплексные числа с положительной действительной частью (неустойчивый фокус). Неустойчивый режим фокального типа. Этот тип движения соответствует периодическим колебаниям с нарастающей амплитудой. В таком случае говорят о режиме самовозбуждающихся колебаний. В реальных системах нарастание амплитуды обычно ограничено физическими процессами, так что возникает устойчивое периодическое движение с постоянной во времени амплитудой. Фазовая траектория при этом накручивается на предельный цикл, соответствующий устойчивым автоколебаниям.

д) 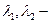 действительные числа, имеющие разные знаки (неустойчивое седло). Неустойчивый режим типа седла. При малом отклонении от положения равновесия система начинает от него удаляться в неустойчивом направлении. В том случае, если решения должны быть конечными, всегда существует два новых стабильных равновесных состояния, к которым приближается система. В свою очередь, существование двух устойчивых состояний позволяет создать систему типа триггера. Он может находиться в одном из двух своих устойчивых состояний A или B бесконечно долго. Внешним возбуждением достаточной амплитуды можно переводить систему из одного устойчивого состояния в другое. Схематически фазовый портрет триггера представлен на рис.
действительные числа, имеющие разные знаки (неустойчивое седло). Неустойчивый режим типа седла. При малом отклонении от положения равновесия система начинает от него удаляться в неустойчивом направлении. В том случае, если решения должны быть конечными, всегда существует два новых стабильных равновесных состояния, к которым приближается система. В свою очередь, существование двух устойчивых состояний позволяет создать систему типа триггера. Он может находиться в одном из двух своих устойчивых состояний A или B бесконечно долго. Внешним возбуждением достаточной амплитуды можно переводить систему из одного устойчивого состояния в другое. Схематически фазовый портрет триггера представлен на рис.


е) 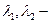 чисто мнимые числа (устойчивый «центр»). Устойчивый режим движения центрального типа. Поскольку в этом случае оба корня чисто мнимые, наблюдаются незатухающие колебания и фазовая траектория системы представляет собой эллипс. Типичный пример такой системы – одномерный гармонический осциллятор без трения.
чисто мнимые числа (устойчивый «центр»). Устойчивый режим движения центрального типа. Поскольку в этом случае оба корня чисто мнимые, наблюдаются незатухающие колебания и фазовая траектория системы представляет собой эллипс. Типичный пример такой системы – одномерный гармонический осциллятор без трения.


Возьмем на фазовой плоскости простую замкнутую кривую N, не содержащую особых
точек. Возьмем на этой кривой точку S и проведем через нее вектор, совпадающий с
направлением касательной к фазовой траектории, проходящей через эту точку. Если точку S двигать вдоль кривой N, вектор касательной к фазовой траектории будет непрерывно вращаться. Когда точка S сделает полный оборот по замкнутой кривой N, вектор сделает некоторое целое число оборотов, т.е. повернется на угол 2πj, где j – целое число. Направление вращения вектора будем считать положительным, если оно совпадает с направлением, в котором точка S обходит замкнутую кривую N. Для определенности будем считать, что точка S всегда обходит кривую N, совершая оборот против часовой стрелки. Целое число j не зависит от выбора кривой N, замкнутые кривые, содержащие те же состояния равновесия, имеют такое же число j. Целое число j носит название индекса замкнутой кривой N по отношению к рассматриваемому векторному полю. Окружим кривой N какое-либо одно состояние равновесия. В силу того, что индекс j не зависит от формы кривой, а определяется только характером самого состояния равновесия. Поэтому j можно отнести к самой особой точке и говорить об индексе Пуанкаре особой точки.
Справедливы следующие утверждения:
1) Индекс замкнутой кривой, не содержащей внутри себя ни одной особой точки, равен
нулю;
2) Индекс замкнутой кривой. Содержащей внутри себя несколько особых точек, равен
сумме индексов этих точек;
3) Индекс замкнутой кривой, являющейся одновременно замкнутой траекторией
системы, равен +1 (случай центра), т.к. направление вектора каждый раз совпадает с направлением касательной к кривой N;
4) Индекс замкнутой кривой, вдоль которой векторы фазовых траекторий направлены либо все внутрь, либо все наружу (замкнутая кривая представляет собой
«цикл без контакта»), равен +1 (случай узла).
3. Формулы Гаусса-Остроградского и Стокса.
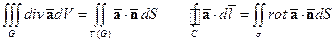




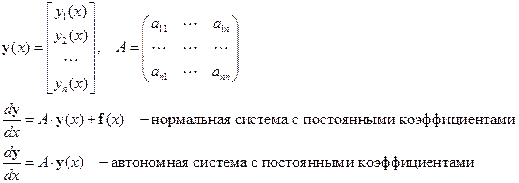
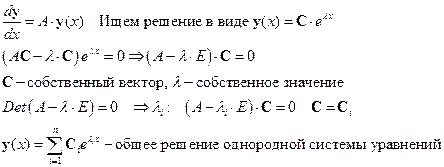
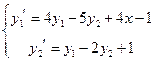
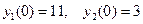 .
.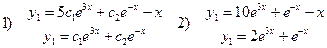



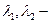 действительные, отрицательные числа (устойчивый узел).
действительные, отрицательные числа (устойчивый узел).