

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Оснащения врачебно-сестринской бригады.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
Линейные отображения, операции с матрицами, решение систем линейных алгебраических уравнений. Теорема о неявной функции.
Пример: Найти первую и вторую производную функции 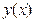 , заданной неявно:
, заданной неявно:  в точке
в точке 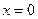 . Найти максимум и минимум функции выделенной явной функции.
. Найти максимум и минимум функции выделенной явной функции.
Решение
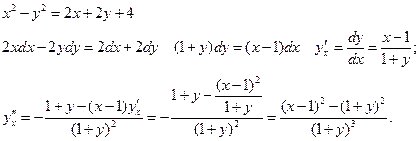
Свойства производной аналитической функции и интеграл Коши. Простейшие конформные отображения. Ряды Тейлора и Лорана.
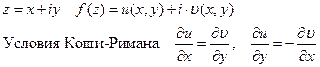
Для любого замкнутого контура 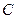 в ограниченной области
в ограниченной области 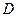 для аналитической функции
для аналитической функции 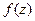 справедливо равенство
справедливо равенство
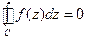 .
.
Интегральная формула Коши
Пусть функция  аналитическая как на самом замкнутом контуре
аналитическая как на самом замкнутом контуре 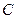 , так и внутри области
, так и внутри области 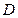 , ограниченной этим контуром. Тогда для любой точки
, ограниченной этим контуром. Тогда для любой точки 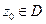 справедливо представление
справедливо представление
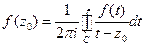 .
.
Произвольная аналитическая функция 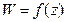 отображает плоскость
отображает плоскость 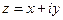 в плоскость
в плоскость 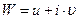 .
.
Геометрический смысл производной данной функции: Если производная аналитической функции 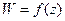 отлична от нуля в точке
отлична от нуля в точке 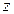 , то аргумент производной равен углу поворота прямой в области
, то аргумент производной равен углу поворота прямой в области 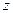 , при отображении этой прямой на плоскость
, при отображении этой прямой на плоскость 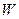 , т.е. углы при отображении в локальной точке не меняются. Модуль производной является коэффициентом подобия.
, т.е. углы при отображении в локальной точке не меняются. Модуль производной является коэффициентом подобия.
Ряды Тейлора и Лорана.
Для функции 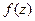 , аналитической в круге с центром в точке
, аналитической в круге с центром в точке 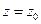 , справедливо разложение в ряд Тейлора
, справедливо разложение в ряд Тейлора
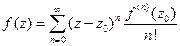 .
.
Для функции 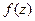 , аналитической внутри кольца
, аналитической внутри кольца 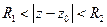 , справедливо разложение в ряд Лорана
, справедливо разложение в ряд Лорана
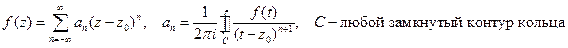
Пример: 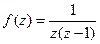 в окрестности точки
в окрестности точки 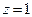 при малых и больших значениях модуля
при малых и больших значениях модуля 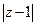 .
.
Представим функцию в следующей форме 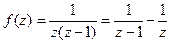 . Функция
. Функция 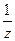 является аналитической внутри круга
является аналитической внутри круга 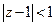 , поэтому раскладывается в ряд Тейлора
, поэтому раскладывается в ряд Тейлора
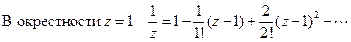 . Функция
. Функция 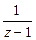 в любом кольце с центром в точке
в любом кольце с центром в точке 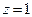 уже разложена в ряд Лорана. Поэтому функция
уже разложена в ряд Лорана. Поэтому функция 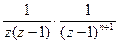 имеет особыми точками полюс первого порядка в точке
имеет особыми точками полюс первого порядка в точке 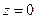 и полюс
и полюс 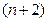 порядка, если
порядка, если 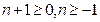 . Для значений
. Для значений 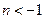 единственной особой точкой остаётся точка
единственной особой точкой остаётся точка 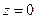 .
.
Если 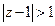 , то в любом кольце с внутренним радиусом, который больше 1, точки
, то в любом кольце с внутренним радиусом, который больше 1, точки 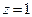 и
и 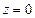 являются полюсами первого порядка. Тогда функция
являются полюсами первого порядка. Тогда функция 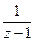 уже разложена в ряд Лорана. Представим функцию
уже разложена в ряд Лорана. Представим функцию 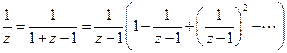 , где ряд, находящийся в скобках сходится.
, где ряд, находящийся в скобках сходится.
Формула Коши
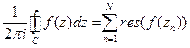
Формула для вычета функции в полюсе порядка m
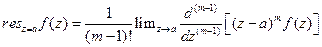
Вычисление интегралов
Пример 1. Вычислить интеграл
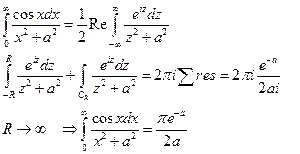
Пример 2. Вычислить интеграл Эйлера 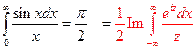 .
.
Пример 3. Вычислить интеграл 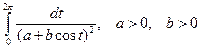 .
.
Положим 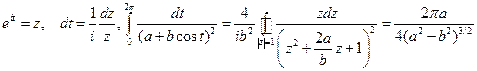
5. Классификация и примеры линейных уравнений с частными производными 2-го порядка. Основные виды начальных и краевых условий. Характеристики линейных уравнений с двумя независимыми переменными.
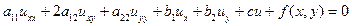
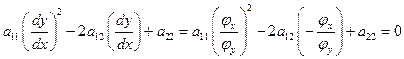
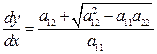 ,
, 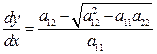
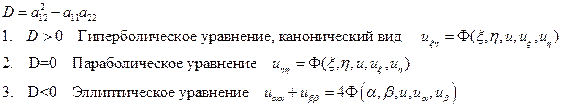
Формула Эйлера для поля скоростей в твердом теле; теоремы сложения скоростей и ускорений для точки; ускорение Кориолиса.
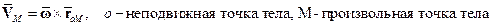
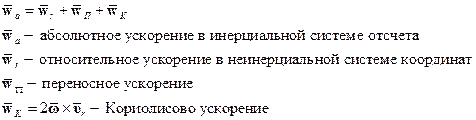
Пример 1: Река течет в южном полушарии в направлении с Севера на Юг. Какой берег реки будет более обрывистым?
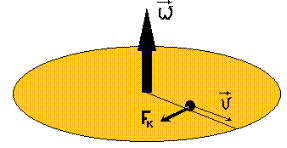
Пример 2: Горизонтально расположенный круглый диск вращается вокруг оси с постоянной угловой скоростью 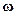 . Муха массой
. Муха массой 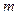 ползёт с постоянной скоростью из центра диска вдоль его радиуса. Чему равна сила Кориолиса, действующая на муху со стороны диска.
ползёт с постоянной скоростью из центра диска вдоль его радиуса. Чему равна сила Кориолиса, действующая на муху со стороны диска.
Внутренние и внешние силы для системы материальных точек. Заданные силы и реакции связей. Теоремы об изменении и законы сохранения импульса, кинетического момента и кинетической энергии системы. Модели сил трения.
Свойства тензоров конечных и малых деформаций. Кинематический смысл компонент тензора скоростей деформации. Кинематические свойства вихрей. Сохранение массы и уравнение неразрывности в переменных Эйлера и Лагранжа.
Массовые и поверхностные силы. Законы изменения импульса и кинетического момента. Симметричность тензора напряжений. Дифференциальные уравнения движения сплошной среды. Связь между напряженным состоянием и деформацией. Определяющие соотношения. Замкнутые системы уравнений.
Теорема об изменении кинетической энергии, работа внутренних поверхностных сил. Первый закон термодинамики. Уравнение притока тепла. Вектор потока тепла, закон теплопроводности Фурье. Второй закон термодинамики. Энтропия.
Модели идеальных жидкостей. Постановки задач. Установившиеся течения, интеграл Бернулли. Парадокс Даламбера. Потенциальные течения, интеграл Коши-Лагранжа. Вихревые течения, теоремы Томсона и Лагранжа.
Модель линейного упругого тел, закон Гука, постановки задач теории упругости в перемещениях и напряжениях. Продольные и поперечные волны в изотропной упругой среде. Функция напряжений плоского напряженного состояния. Задача Ламе о толстостенной трубе.
Модель линейно упругой среды:
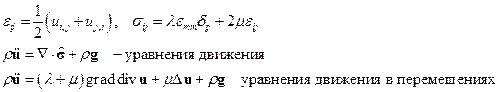
Постановка задач. На границе упругого тела задан вектор напряжений. Задача в напряжениях: 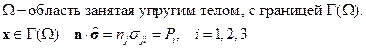
На границе упругого тела задан вектор перемещений – задача в перемещениях
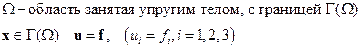
Плоская статическая задача теории упругости. Функция напряжений.
Рассмотрим два случая напряжённого состояния.
1.Случай плоско-деформированного состояния, когда 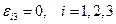 (это состояние реализуется при плоскопараллельном движении среды).
(это состояние реализуется при плоскопараллельном движении среды).
В этом случае из закона Гука следует, что отличными от нуля напряжениями будут  .
.
Закон Гука может быть переписан в форме
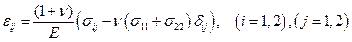 . (1)
. (1)
2.Случай плосконапряжённого состояния, когда 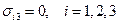 (это состояние приближённо реализуется для тонких пластин).
(это состояние приближённо реализуется для тонких пластин).
Закон Гука может быть переписан в форме
 . (2)
. (2)
В плоском случае уравнения равновесия имеют вид
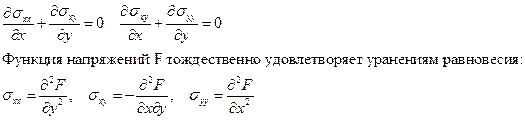
Для получения уравнения воспользуемся условиями совместности деформаций. В плосконапряженном случае получим
 .
.
В результате подстановки деформаций и напряжений получим для функции напряжений
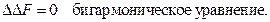
Волны в упругой среде.
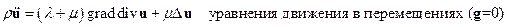
Разложим векторное поле перемещений в форме Ламе 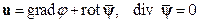 .
.
После применения операции  и операции
и операции 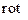 к уравнениям движения, получим
к уравнениям движения, получим
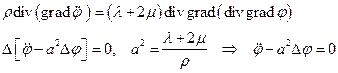
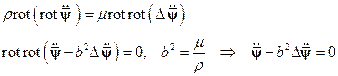
Теория течения:
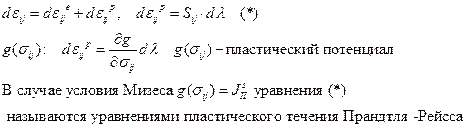
Линейные отображения, операции с матрицами, решение систем линейных алгебраических уравнений. Теорема о неявной функции.
Пример: Найти первую и вторую производную функции 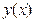 , заданной неявно:
, заданной неявно:  в точке
в точке 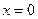 . Найти максимум и минимум функции выделенной явной функции.
. Найти максимум и минимум функции выделенной явной функции.
Решение
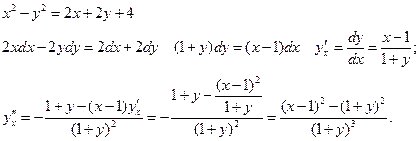

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!