Построение решений дифференциальных уравнений в виде степенных рядов
Содержание
Введение
1. Понятие о голоморфном решении задачи Коши
2. Теорема Коши о существовании и единственности голоморфного решения задачи Коши
2.1 Теорема Коши
2.2 Случай линейного уравнения. Выбор начальных данных. Радиус сходимости ряда, представляющего решение
3. Решение задачи Коши для линейного уравнения второго порядка при помощи степенных рядов
4. Интегрирование однородного линейного уравнения второго порядка при помощи степенных рядов
5. Интегрирование дифференциальных уравнений при помощи степенных рядов
6. Уравнение Бесселя
Заключение
Список использованных источников
Введение
Дифференциальным уравнением называется равенство, содержащее независимые переменные, искомую функцию и её производные. При этом независимые переменные всегда предполагаются вещественными, а рассматриваемые функции - вещественными и однозначными. Порядок старшей производной, входящей в состав уравнения, называется порядком уравнения. Если независимая переменная только одна, то уравнение называется обыкновенным. В противном случае оно называется уравнением с частными производными. В теории дифференциальных уравнений изучаются также системы дифференциальных уравнений.
Теоретической основой нахождения решений дифференциальных уравнений в виде степенных рядов является теорема Коши о существовании и единственности голоморфного решения задачи Коши.
Ввиду большой важности многих дифференциальных линейных уравнений второго порядка для приложений, в тех случаях, когда их интегрирование при помощи элементарных функций не удаётся, их решения вводятся в качестве новых трансцендентных функций. Таковы, например, функции Бесселя первого и второго рода - два линейно независимых решения уравнения Бесселя. Для определения этих функций часто пользуются представлением решения уравнения в виде степенного ряда по возрастающим степеням  , где
, где  - начальное значение. В аналитической теории дифференциальных уравнений доказывается, что если коэффициенты
- начальное значение. В аналитической теории дифференциальных уравнений доказывается, что если коэффициенты  уравнения
уравнения  являются многочленами или степенными рядами из целых неотрицательных степеней
являются многочленами или степенными рядами из целых неотрицательных степеней  , причём
, причём  не равно нулю, то решения уравнения
не равно нулю, то решения уравнения  тоже выражаются сходящимися степенными рядами по целым неотрицательным степеням
тоже выражаются сходящимися степенными рядами по целым неотрицательным степеням  . Не доказывая здесь этого общего положения, мы сумеем в каждом отдельном случае доказать сходимость рядов, представляющих решения данного уравнения.
. Не доказывая здесь этого общего положения, мы сумеем в каждом отдельном случае доказать сходимость рядов, представляющих решения данного уравнения.
задача коши дифференциальное уравнение
Пример 1.
Функции  ,
,  ,
,  голоморфны в точке
голоморфны в точке 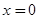 , т.к. известно:
, т.к. известно:
 ,
,  ,
, 
Причём ряды справа сходятся при  .
.
Пример 2.
Полином от  ,
,  ,
,  ,
,  - целые функции. В частности, при
- целые функции. В частности, при 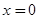 имеем известные разложения:
имеем известные разложения:

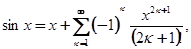
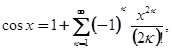
Причём ряды справа сходятся при всех 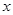 .
.
Пример 3.
Функция  является голоморфной в точке
является голоморфной в точке 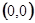 , т.к.
, т.к.

Причём ряд справа сходится в области  .
.
Важным частным случаем голоморфных функций являются функции, для которых представление (1.1) имеет место в окрестности любой точки  , а ряд сходится при всех значениях
, а ряд сходится при всех значениях  . Такие функции называются целыми. (Пример 2.)
. Такие функции называются целыми. (Пример 2.)
Данное выше определение голоморфности функции  распространяется на случай функции
распространяется на случай функции  , зависящей от n независимых переменных. Последняя называется голоморфной в точке
, зависящей от n независимых переменных. Последняя называется голоморфной в точке  , если
, если

Где ряд справа сходится в области 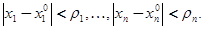 (пример 3.)
(пример 3.)
Вернёмся к функции  , зависящей от одной независимой переменной. Из теории степенных рядов известно, что если
, зависящей от одной независимой переменной. Из теории степенных рядов известно, что если  допускает разложение (1.1), то это разложение единственно; причём коэффициенты
допускает разложение (1.1), то это разложение единственно; причём коэффициенты  выражаются через значения
выражаются через значения  и её производных в точке
и её производных в точке  по известным формулам
по известным формулам


Поэтому разложение (1.1) можно переписать в виде
 (1.2)
(1.2)
Ряд справа называется рядом Тейлора для функции  в точке
в точке  .
.
Таким образом, всякий сходящийся степенной ряд Тейлора для своей суммы, и мы можем говорить, что функция  голоморфна в точке
голоморфна в точке  , если она допускает в окрестности этой точки разложение в ряд Тейлора. В частности, функция
, если она допускает в окрестности этой точки разложение в ряд Тейлора. В частности, функция  , для которой имеет место разложение
, для которой имеет место разложение

голоморфна в точке 0.
Из разложения (1.2) следует, что функция  , голоморфная в точке
, голоморфная в точке  , допускает следующее асимптотическое представление при
, допускает следующее асимптотическое представление при  :
:

Где 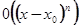 - бесконечно малая функция при
- бесконечно малая функция при  более высокого порядка малости, чем
более высокого порядка малости, чем  .
.
В частности, при  имеем асимптотическое представление
имеем асимптотическое представление

Отбросив все члены ряда Тейлора (1.2), кроме свободного и члена с первой степенью разности  , получаем линеаризацию функции
, получаем линеаризацию функции  в точке
в точке  :
:
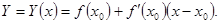 (1.3)
(1.3)
Геометрически (рис. 1.1) здесь речь идёт о замене отрезка графика функции  в достаточно малой окрестности точки
в достаточно малой окрестности точки  отрезком касательной (1.3) к нему в точке
отрезком касательной (1.3) к нему в точке 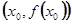 ,
,  Совершаемая при этом погрешность будет иметь порядок
Совершаемая при этом погрешность будет иметь порядок 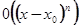 при
при  , т.е. является бесконечно малой функцией при
, т.е. является бесконечно малой функцией при  более высокого порядка малости, чем
более высокого порядка малости, чем  .
.


Рис. 1.1 Рис. 1.2
Обратимся теперь к задаче Коши.
Рассмотрим сначала задачу Коши для уравнения первого порядка в нормальной форме:
 (1.4)
(1.4)
Говорят, что задача (1.4) имеет решение
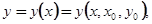 (1.5)
(1.5)
голоморфное в точке 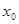 (т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке
(т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке 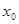 , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):

Или
 (1.6)
(1.6)
(здесь свободный член  есть начальное значение решения (1.5) при
есть начальное значение решения (1.5) при  ).
).
Линеаризация решения задачи Коши (1.4) в точке  имеет вид
имеет вид

Или

(т.к.  ).
).
Рассмотрим пример, в котором решение задачи Коши представимо в виде сходящегося степенного ряда.
Пример 4.
Найти голоморфное решение задачи Коши
 (1.7)
(1.7)
т.е. нужно найти функцию, которая удовлетворяла бы начальному условию 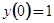 , дифференциальному уравнению
, дифференциальному уравнению  легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням
легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням 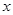 .
.
Интегрируя уравнение  , имеем
, имеем
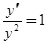

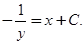
Удовлетворяя начальному условию 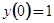 , находим, что
, находим, что  . Следовательно, искомым решением будет
. Следовательно, искомым решением будет
 (1.8)
(1.8)
Это решение представимо в окрестности начального значения  , т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
, т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
 (1.9)
(1.9)
Заметим, что решение (1.8) определено в более широком интервале  , так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал
, так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал 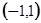 .
.
Линеаризацией в точке 0 будет

(см. рис. 1.2).
Для непосредственного нахождения голоморфного решения поставленной задачи Коши (1.7) можно использовать либо метод последовательного дифференцирования данного дифференциального уравнения, основанный на представлении решения в виде ряда Тейлора (ибо всякий сходящийся степенной ряд есть ряд Тейлора для его суммы), либо метод неопределенных коэффициентов. Рассмотрим оба эти метода.
Представляя искомое решение в виде ряда Тейлора по степеням  , имеем
, имеем
 (1.10)
(1.10)
Свободный член 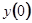 нам известен из начального условия
нам известен из начального условия  . Коэффициент при
. Коэффициент при  можно найти из дифференциального уравнения
можно найти из дифференциального уравнения  , положив в его обеих частях
, положив в его обеих частях  ; приняв во внимание начальное условие
; приняв во внимание начальное условие  , получим
, получим
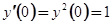 .
.
Далее, дифференцируя обе части уравнения  по
по  (при этом
(при этом  рассматривается как сложная функция от
рассматривается как сложная функция от  ), имеем:
), имеем:
 (1.11)
(1.11)
Полагая здесь  и заменяя y и
и заменяя y и  их значениями при
их значениями при  , получим
, получим

Дифференцируя (1.11) по  , найдем:
, найдем:
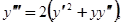
Откуда, полагая  , получим
, получим

Аналогично найдем,  Подставляя значение
Подставляя значение  и найденные значения производных от у в точке
и найденные значения производных от у в точке  в (1.10), получим снова разложение (1.9).
в (1.10), получим снова разложение (1.9).
В методе неопределенных коэффициентов голоморфное решение задачи Коши (1.7) ищется согласно (1.6) в виде
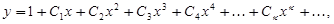 (1.12)
(1.12)
Где  - неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение
- неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение  и приравниванием коэффициентов при одинаковых степенях
и приравниванием коэффициентов при одинаковых степенях  в левой и правой частях полученного равенства (предполагая, что ряд (1.12) сходится, и, используя известную теорему о тождестве степенных рядов). Имеем
в левой и правой частях полученного равенства (предполагая, что ряд (1.12) сходится, и, используя известную теорему о тождестве степенных рядов). Имеем

Подставляя (1.12) в 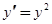 , получим
, получим

Выполняя, справа операцию возведения степенного ряда в квадрат, получим

Приравняем коэффициенты при одинаковых степенях  :
:

Определяя отсюда последовательно  найдем,
найдем,  Подставляя найденные значения
Подставляя найденные значения  в ряд (1.12), получим искомое решение в виде (1.9).
в ряд (1.12), получим искомое решение в виде (1.9).
Рассмотрим теперь задачу Коши для уравнения n-го порядка в нормальной форме
 (1.13)
(1.13)
Говорят, что задача (1.13) имеет решение
 (1.14)
(1.14)
Голоморфное в точке 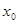 , если функция (1.14) голоморфна в точке
, если функция (1.14) голоморфна в точке  , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):

Или
 (1.15)
(1.15)
(Здесь  заданные начальные значения решения (1.13) при
заданные начальные значения решения (1.13) при  ). Коэффициенты
). Коэффициенты  так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
Заметим, что формула (1.6) есть частный случай формулы (1.15) при n = 1. В этом последнем случае нам заранее известно лишь одно первое слагаемое 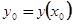 . Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
. Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
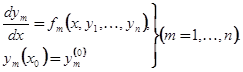 (1.16)
(1.16)
Решение этой задачи
 (1.17)
(1.17)
Называется голоморфным в точке  , если все функции (1.17) голоморфны в этой точке. Оно имеет вид
, если все функции (1.17) голоморфны в этой точке. Оно имеет вид
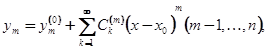
Где  - заданные числа (начальные значения искомых функций
- заданные числа (начальные значения искомых функций  ).
).
Теорема Коши
Начнем с уравнения первого порядка в нормальной форме. Пусть поставлена задача Коши (1.4)

Оказывается, если функция  голоморфна в точке
голоморфна в точке  , то задача Коши (1.4) имеет голоморфное в точке
, то задача Коши (1.4) имеет голоморфное в точке  решение, и притом единственное. Это решение имеет вид (1.6),
решение, и притом единственное. Это решение имеет вид (1.6),
Можно считать начальные данные  ,
,  нулевыми (
нулевыми ( = 0,
= 0,  = 0), ибо этого всегда можно добиться преобразованием
= 0), ибо этого всегда можно добиться преобразованием 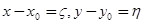 . Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу
. Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу
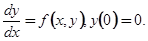 (2.1.1)
(2.1.1)
Теорема Коши. Если  голоморфна в точке (0, 0), т.е. допускает разложение
голоморфна в точке (0, 0), т.е. допускает разложение
 ( 2.1.2)
( 2.1.2)
То задача Коши (2.1.1) имеет единственное решение, голоморфное в точке 0:
 (2.1.3)
(2.1.3)
Доказательство. Утверждение теоремы, будет доказано, если покажем, что все коэффициенты Сk могут быть найдены ( единственным образом) и что ряд ( 2.1.3) сходится в указанной окрестности точки 0. В связи с этим разобьем доказательство на две части.
Часть 1 (построение (единственного) формального решения (2.1.3)). Будем искать (2.1.3) методом неопределенных коэффициентов. Подставляя ряд (2.1.3) в уравнение
 (2.1.4)
(2.1.4)
Получим
 (2.1.5)
(2.1.5)
(Здесь выполнены формальные операции почленного дифференцирования степенного ряда и подстановки ряда в ряд, законность которых следует из сходимости ряда (2.1.3), которую мы восстановим во второй части доказательства.)
Считая равенство (2.1.5) тождеством (т.к.2.1.3) - решение дифференциального уравнения (2.1.4) и приравнивая коэффициенты при одинаковых степенях  , будем иметь
, будем иметь

Мы видим, что С1 и С2 выражены через некоторые первые коэффициенты разложения функции  .
.
Аналогично, приравнивая в (2.1.5) коэффициенты при  , найдем
, найдем
 (2.1.6)
(2.1.6)
Где Рk - полиномы от своих аргументов с положительными коэффициентами (у Р2 эти коэффициенты равны  ).
).
Таким образом, формальное решение (2.1.3) построено. Из единственности определения Сk следует, что если голоморфное решение задачи Коши (1.4) существует, то оно единственно.
Часть 2. Докажем теперь, что ряд (2.1.3) сходится в некоторой окрестности точки 0. Для этого достаточно построить степенной ряд, мажорирующий ряд (2.1.3), т.е. ряд
 (2.1.7)
(2.1.7)
С положительными коэффициентами, сходящийся в некоторой области
 (2.1.8)
(2.1.8)
И такой, что
 (2.1.9)
(2.1.9)
Тогда, как известно, ряд (2.1.3) будет заведомо сходиться в той же области (2.1.8)
Для построения ряда (2.1.7) рассмотрим мажорантную задачу Коши:
 (2.1.10)
(2.1.10)
Где  - некоторая мажоранта функции
- некоторая мажоранта функции  . В качестве
. В качестве  возьмем мажоранту Коши
возьмем мажоранту Коши

Где,  а M - сумма ряда
а M - сумма ряда
 (2.1.11)
(2.1.11)
(который сходится вследствие абсолютной сходимости ряда (2.1.2) в области  ), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2)
), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2)
 (2.1.12)
(2.1.12)
Вытекающей из (2.1.11).
Взяв ряд по степеням  и y с коэффициентом А тп, получим
и y с коэффициентом А тп, получим

Мажорантная задача Коши (2.1.10) примет вид
 (2.1.13)
(2.1.13)
Дифференциальное уравнение, входящее в задачу (2.1.13), называется мажорантным уравнением для уравнения задачи (1.4)
Мажорантная задача (2.1.13) имеет единственное решение. Найдём его.
Интегрируя мажорантное уравнение, имеем
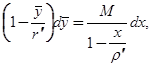 ,
,  (2.1.14)
(2.1.14)
Удовлетворяя начальному условию 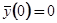 , найдем
, найдем  . Подставляя это значение С в (2.1.14) и умножая обе части на
. Подставляя это значение С в (2.1.14) и умножая обе части на  , получим
, получим
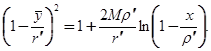
Разрешая относительно 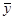 , найдем
, найдем
 (2.1.15)
(2.1.15)
Это решение голоморфно в точке 0 как суперпозиция двух голоморфных функций:

Таким образом, решение (2.1.15) представимо в виде
 (2.1.16)
(2.1.16)
Где ряд справа в некоторой окрестности точки 0 (по определению голоморфной функции). Оценим область сходимости ряда (2.1.16).
Согласно известной теореме Абеля достаточно ограничиться исследованием положительных значений  . Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения
. Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения  должны удовлетворять системе двух неравенств
должны удовлетворять системе двух неравенств
 (2.1.17)
(2.1.17)
Последнее неравенство следует из неравенства  с учётом того, что
с учётом того, что 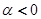
Решая второе из неравенств (2.1.17), имеем

Первое из неравенств (2.1.17) выполняется автоматически. Таким образом, ряд (2.1.16) сходится в области

Остается показать, что все коэффициенты ряда (2.1.16) положительны и что имеют место оценки (2.1.9).
Но это следует из того, что  можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим
можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим
 (2.1.6 ‘)
(2.1.6 ‘)
Где Pk - те же самые полиномы, что и в (2.1.6), только аргументы другие: не коэффициенты разложения функции  , а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все
, а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все  положительны и мажорируют Ck, т.е. имеют место оценки (2.1.9). Мажорирующий ряд (2.1.7) построен.
положительны и мажорируют Ck, т.е. имеют место оценки (2.1.9). Мажорирующий ряд (2.1.7) построен.
Таким образом, ряд (2.1.16) мажорирует формальное решение (2.1.3), чем завершается доказательство теоремы Коши.
Пример 6.
Проинтегрировать при помощи степенных рядов уравнение

Построим сначала голоморфный базис (у1, у2), нормированный в точке 0, которая (как и любая точка  ) является точкой голоморфности коэффициента при у. Теорема Коши для случая линейного уравнения гарантирует существование и единственность этого базиса (как, впрочем, и любо другого); причем ряды, представляющие функции у1 и у2, заведомо сходятся при всех
) является точкой голоморфности коэффициента при у. Теорема Коши для случая линейного уравнения гарантирует существование и единственность этого базиса (как, впрочем, и любо другого); причем ряды, представляющие функции у1 и у2, заведомо сходятся при всех  , представляя, таким образом, целые функции. Нам остается только построить у1 и у2.
, представляя, таким образом, целые функции. Нам остается только построить у1 и у2.
Строим у1 в виде
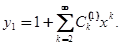
Будем искать Сk методом последовательного дифференцирование, рассматривая их как коэффициенты Тейлора для функции у1

Дело сводится, таким образом, к нахождению  .
.
Из тождества
 (4.2)
(4.2)
Находим

Дифференцируя (4.2), имеем

Откуда
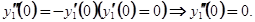
Далее, имеем

Легко видеть, что

Поэтому

Аналогично найдем
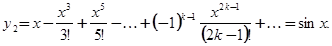
Как и следовало ожидать, ряды для у1, у2 сходятся при всех  , а их сумы
, а их сумы  и
и  - целые функции.
- целые функции.
Легко непосредственной проверкой убедиться, что функция  и
и  образуют голоморфный в точке 0 базис, нормированный в этой точке.
образуют голоморфный в точке 0 базис, нормированный в этой точке.
Используя найденный голоморфный базис, получаем общее решение

В области
 (4.3)
(4.3)
Пример 7. Построить фундаментальную систему решений уравнения
 (4.4)
(4.4)
нормированную в точке 0 в виде степенных рядов.
Известно, что уравнение (4.4) имеет фундаментальную систему решений  .
.
Оба эти решения голоморфны в точке 0. Но эта фундаментальная система не нормирована в точке 0.
Для построения нормированной в точке 0 фундаментальной систему у1, у2 можно воспользоваться общим решением
 (4.5)
(4.5)
Получим  .
.
Найдем эту фундаментальную систему непосредственно.
Имеем

Поэтому

Аналогично находим

Снова получили ту же самую фундаментальную систему, чего и следовало ожидать, в силу единственности фундаментальной системы решений, нормированный в данной точке.
Используя фундаментальную систему  , можем записать обще решение уравнения (4.4) в виде
, можем записать обще решение уравнения (4.4) в виде

Это общее решение, так же как и общее решение (4.5), определено в области (4.3).
Пример 8.
Найти общее решение уравнения 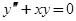 .
.
Ищем это решение в виде степенного ряда по степеням 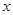 :
:
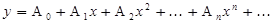
Формальным дифференцированием находим:
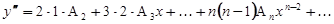
Подставляем в уравнение и приравниваем коэффициенты при одинаковых степенях 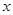 :
:
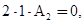
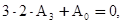
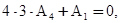
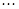
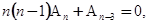
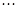
Из этих уравнений находим:
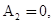
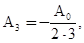
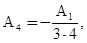
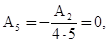
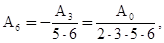
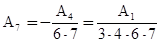
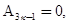
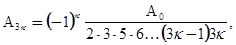
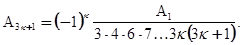
Коэффициенты 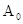 и
и 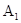 не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид:
не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид:
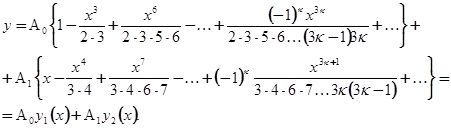
С помощью элементарных признаков легко установить сходимость рядов 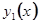 и
и 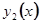 для всех значений
для всех значений 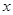 ; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси
; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси 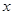 . Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.
. Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.
Метод интегрирования линейных дифференцированных уравнений рядами, расположенными по степеням 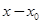 , применим также в некоторых случаях, когда коэффициент
, применим также в некоторых случаях, когда коэффициент 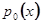 обращается в нуль при
обращается в нуль при 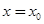 . Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени
. Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени 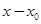 , а имеет вид:
, а имеет вид:
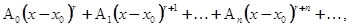 (5.1)
(5.1)
где r - некоторое число, вообще не целое. Уже из (5.1) ясно, что полное значение такого разложения может обнаружиться лишь при рассмотрении х как комплексного переменного, так как при 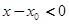 и дробном или иррациональном r выражение
и дробном или иррациональном r выражение  в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от
в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от 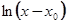 на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.
на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.
Рассмотрим уравнение вида:
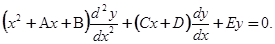 (5.2)
(5.2)
Корни многочлена второй степени, стоящего множителем при  , пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную
, пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную 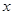 в комплексной области). Чтобы не вводить мнимых величин, мы предположим также, что А, В, C, D, E - действительные числа. В таком случае можно переписать уравнение (5.2) в виде:
в комплексной области). Чтобы не вводить мнимых величин, мы предположим также, что А, В, C, D, E - действительные числа. В таком случае можно переписать уравнение (5.2) в виде:
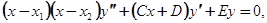 (5.2’)
(5.2’)
где 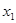 и
и 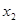 - корни многочлена
- корни многочлена 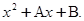 Это показывает, что коэффициент при
Это показывает, что коэффициент при 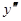 обращается в нуль при значениях
обращается в нуль при значениях 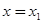 и
и 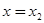 . Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с
. Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с 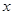 соотношением:
соотношением:
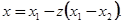
Тогда
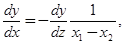
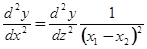 ,
,
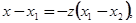
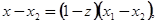
и мы получаем:
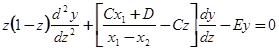 .
.
Вводя обозначения 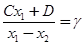 , C=α+β+1, E=αβ и обозначения независимое переменное снова через
, C=α+β+1, E=αβ и обозначения независимое переменное снова через 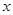 , мы получим гипергеометрическое уравнение в обычном его виде:
, мы получим гипергеометрическое уравнение в обычном его виде:
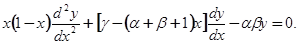 (5.3)
(5.3)
Пример 9.
Привести к виду (5.3) уравнение Лежандра 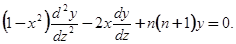 замена переменного
замена переменного 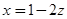 дает:
дает:
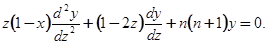
Здесь 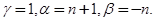
Мы видим, что уравнение (5.3) зависит от трех параметров: α, β, γ, причем параметры α и β входят симметрично. Найдем решения уравнения (5.3) в виде рядов по степеням 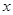 . подставляем в уравнение ряды:
. подставляем в уравнение ряды:
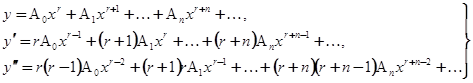 (5.4)
(5.4)
последний из рядов (5.4) умножаем на 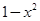 , второй ряд - на
, второй ряд - на 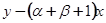 , третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях
, третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях 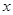 и приравниваем их к нулю. Низшая степень
и приравниваем их к нулю. Низшая степень 
|
|
|



 , где
, где  - начальное значение. В аналитической теории дифференциальных уравнений доказывается, что если коэффициенты
- начальное значение. В аналитической теории дифференциальных уравнений доказывается, что если коэффициенты 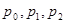 уравнения
уравнения  являются многочленами или степенными рядами из целых неотрицательных степеней
являются многочленами или степенными рядами из целых неотрицательных степеней  не равно нулю, то решения уравнения
не равно нулю, то решения уравнения  ,
,  ,
,  голоморфны в точке
голоморфны в точке 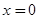 , т.к. известно:
, т.к. известно: ,
,  ,
, 
 .
.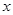 ,
,  ,
,  ,
,  - целые функции. В частности, при
- целые функции. В частности, при 
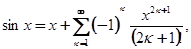
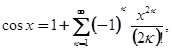
 является голоморфной в точке
является голоморфной в точке 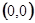 , т.к.
, т.к.
 .
. , а ряд сходится при всех значениях
, а ряд сходится при всех значениях  распространяется на случай функции
распространяется на случай функции  , зависящей от n независимых переменных. Последняя называется голоморфной в точке
, зависящей от n независимых переменных. Последняя называется голоморфной в точке  , если
, если
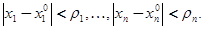 (пример 3.)
(пример 3.) выражаются через значения
выражаются через значения 

 (1.2)
(1.2)
 :
:
 - бесконечно малая функция при
- бесконечно малая функция при  .
. имеем асимптотическое представление
имеем асимптотическое представление
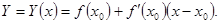 (1.3)
(1.3) в достаточно малой окрестности точки
в достаточно малой окрестности точки 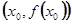 ,
,  Совершаемая при этом погрешность будет иметь порядок
Совершаемая при этом погрешность будет иметь порядок 

 (1.4)
(1.4)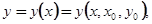 (1.5)
(1.5)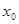 (т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке
(т.е. при начальном значении независимой переменной), если функция (1.5) голоморфна в точке 
 (1.6)
(1.6) есть начальное значение решения (1.5) при
есть начальное значение решения (1.5) при  ).
). имеет вид
имеет вид

 ).
). (1.7)
(1.7)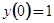 , дифференциальному уравнению
, дифференциальному уравнению  легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням
легко интегрируется, то мы сначала найдём искомое решение, а потом попытаемся представить его в виде ряда по степеням 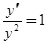

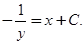
 . Следовательно, искомым решением будет
. Следовательно, искомым решением будет (1.8)
(1.8) , т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом:
, т.е. в окрестности нуля, известным степенным рядом, а именно геометрическим рядом: (1.9)
(1.9) , так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал
, так что ряд (1.9) дает аналитическое представление не всего решения (1.8), а лишь сужения его на интервал 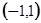 .
.
 , имеем
, имеем (1.10)
(1.10)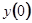 нам известен из начального условия
нам известен из начального условия  . Коэффициент при
. Коэффициент при  ; приняв во внимание начальное условие
; приняв во внимание начальное условие 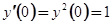 .
. (при этом
(при этом  рассматривается как сложная функция от
рассматривается как сложная функция от  (1.11)
(1.11) их значениями при
их значениями при 
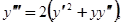

 Подставляя значение
Подставляя значение  и найденные значения производных от у в точке
и найденные значения производных от у в точке 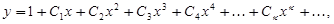 (1.12)
(1.12) - неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение
- неопределенные коэффициенты, значения которых определяются подстановкой (1.12) в дифференциальное уравнение  и приравниванием коэффициентов при одинаковых степенях
и приравниванием коэффициентов при одинаковых степенях 
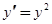 , получим
, получим


 найдем,
найдем,  Подставляя найденные значения
Подставляя найденные значения  (1.13)
(1.13) (1.14)
(1.14)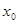 , если функция (1.14) голоморфна в точке
, если функция (1.14) голоморфна в точке  , т.е. представима в виде (1.1):
, т.е. представима в виде (1.1):
 (1.15)
(1.15) заданные начальные значения решения (1.13) при
заданные начальные значения решения (1.13) при  ). Коэффициенты
). Коэффициенты  так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.
так же, как и в случае построения голоморфного решения задачи Коши для уравнения первого порядка, могут быть найдены из самого дифференциального уравнения и уравнений, полученных из него последовательным дифференцированием, или методом неопределенных коэффициентов.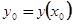 . Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений
. Обратимся, наконец, к задаче Коши для нормальной системы дифференциальных уравнений (1.16)
(1.16) (1.17)
(1.17) , если все функции (1.17) голоморфны в этой точке. Оно имеет вид
, если все функции (1.17) голоморфны в этой точке. Оно имеет вид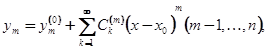
 - заданные числа (начальные значения искомых функций
- заданные числа (начальные значения искомых функций  ).
).
 голоморфна в точке
голоморфна в точке  , то задача Коши (1.4) имеет голоморфное в точке
, то задача Коши (1.4) имеет голоморфное в точке  нулевыми (
нулевыми ( = 0,
= 0, 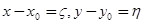 . Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу
. Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу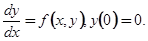 (2.1.1)
(2.1.1) ( 2.1.2)
( 2.1.2) (2.1.3)
(2.1.3) (2.1.4)
(2.1.4) (2.1.5)
(2.1.5)
 , найдем
, найдем (2.1.6)
(2.1.6) ).
). (2.1.7)
(2.1.7) (2.1.8)
(2.1.8) (2.1.9)
(2.1.9) (2.1.10)
(2.1.10) - некоторая мажоранта функции
- некоторая мажоранта функции  . В качестве
. В качестве  возьмем мажоранту Коши
возьмем мажоранту Коши
 а M - сумма ряда
а M - сумма ряда (2.1.11)
(2.1.11) ), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2)
), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2) (2.1.12)
(2.1.12) и y с коэффициентом А тп, получим
и y с коэффициентом А тп, получим
 (2.1.13)
(2.1.13)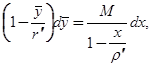 ,
,  (2.1.14)
(2.1.14)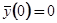 , найдем
, найдем  . Подставляя это значение С в (2.1.14) и умножая обе части на
. Подставляя это значение С в (2.1.14) и умножая обе части на  , получим
, получим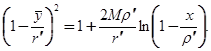
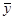 , найдем
, найдем (2.1.15)
(2.1.15)
 (2.1.16)
(2.1.16) . Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения
. Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения  (2.1.17)
(2.1.17) с учётом того, что
с учётом того, что 


 можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим
можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим (2.1.6 ‘)
(2.1.6 ‘) , а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все
, а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все 
 ) является точкой голоморфности коэффициента при у. Теорема Коши для случая линейного уравнения гарантирует существование и единственность этого базиса (как, впрочем, и любо другого); причем ряды, представляющие функции у1 и у2, заведомо сходятся при всех
) является точкой голоморфности коэффициента при у. Теорема Коши для случая линейного уравнения гарантирует существование и единственность этого базиса (как, впрочем, и любо другого); причем ряды, представляющие функции у1 и у2, заведомо сходятся при всех  , представляя, таким образом, целые функции. Нам остается только построить у1 и у2.
, представляя, таким образом, целые функции. Нам остается только построить у1 и у2.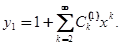

 .
. (4.2)
(4.2)

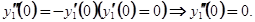



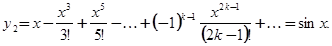
 и
и  - целые функции.
- целые функции. и
и  образуют голоморфный в точке 0 базис, нормированный в этой точке.
образуют голоморфный в точке 0 базис, нормированный в этой точке.
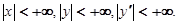 (4.3)
(4.3) (4.4)
(4.4) .
. (4.5)
(4.5) .
.


 , можем записать обще решение уравнения (4.4) в виде
, можем записать обще решение уравнения (4.4) в виде
 .
.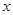 :
: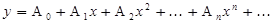
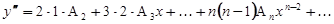
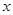 :
: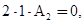
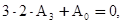
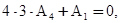
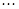
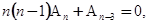
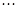
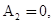
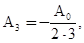
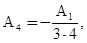
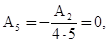
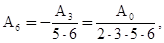
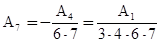
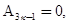
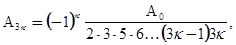
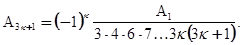
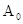 и
и 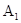 не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид:
не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид: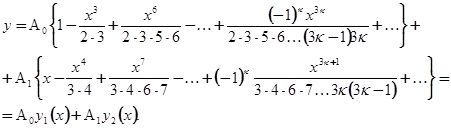
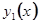 и
и 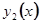 для всех значений
для всех значений 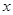 ; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси
; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси 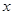 . Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.
. Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.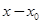 , применим также в некоторых случаях, когда коэффициент
, применим также в некоторых случаях, когда коэффициент 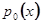 обращается в нуль при
обращается в нуль при 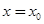 . Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени
. Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени 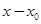 , а имеет вид:
, а имеет вид: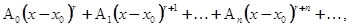 (5.1)
(5.1)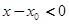 и дробном или иррациональном r выражение
и дробном или иррациональном r выражение 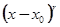 в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от
в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от 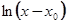 на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.
на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.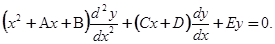 (5.2)
(5.2) , пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную
, пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную 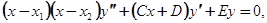 (5.2’)
(5.2’)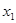 и
и 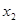 - корни многочлена
- корни многочлена 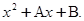 Это показывает, что коэффициент при
Это показывает, что коэффициент при 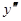 обращается в нуль при значениях
обращается в нуль при значениях 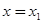 и
и 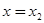 . Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с
. Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с 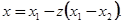
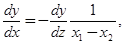
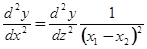 ,
,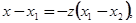
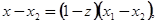
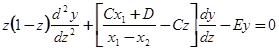 .
.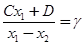 , C=α+β+1, E=αβ и обозначения независимое переменное снова через
, C=α+β+1, E=αβ и обозначения независимое переменное снова через 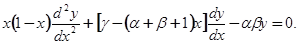 (5.3)
(5.3)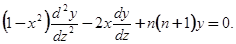 замена переменного
замена переменного 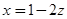 дает:
дает: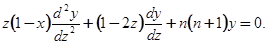
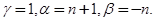
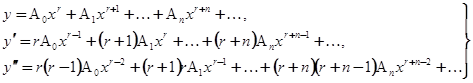 (5.4)
(5.4) , второй ряд - на
, второй ряд - на 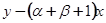 , третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях
, третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях