

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Теорема Коши
Начнем с уравнения первого порядка в нормальной форме. Пусть поставлена задача Коши (1.4)

Оказывается, если функция  голоморфна в точке
голоморфна в точке  , то задача Коши (1.4) имеет голоморфное в точке
, то задача Коши (1.4) имеет голоморфное в точке  решение, и притом единственное. Это решение имеет вид (1.6),
решение, и притом единственное. Это решение имеет вид (1.6),
Можно считать начальные данные  ,
,  нулевыми (
нулевыми ( = 0,
= 0,  = 0), ибо этого всегда можно добиться преобразованием
= 0), ибо этого всегда можно добиться преобразованием 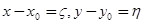 . Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу
. Таким образом, вместо задачи Коши (1.4) мы можем рассматривать задачу
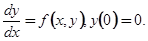 (2.1.1)
(2.1.1)
Теорема Коши. Если  голоморфна в точке (0, 0), т.е. допускает разложение
голоморфна в точке (0, 0), т.е. допускает разложение
 ( 2.1.2)
( 2.1.2)
То задача Коши (2.1.1) имеет единственное решение, голоморфное в точке 0:
 (2.1.3)
(2.1.3)
Доказательство. Утверждение теоремы, будет доказано, если покажем, что все коэффициенты Сk могут быть найдены ( единственным образом) и что ряд ( 2.1.3) сходится в указанной окрестности точки 0. В связи с этим разобьем доказательство на две части.
Часть 1 (построение (единственного) формального решения (2.1.3)). Будем искать (2.1.3) методом неопределенных коэффициентов. Подставляя ряд (2.1.3) в уравнение
 (2.1.4)
(2.1.4)
Получим
 (2.1.5)
(2.1.5)
(Здесь выполнены формальные операции почленного дифференцирования степенного ряда и подстановки ряда в ряд, законность которых следует из сходимости ряда (2.1.3), которую мы восстановим во второй части доказательства.)
Считая равенство (2.1.5) тождеством (т.к.2.1.3) - решение дифференциального уравнения (2.1.4) и приравнивая коэффициенты при одинаковых степенях  , будем иметь
, будем иметь

Мы видим, что С1 и С2 выражены через некоторые первые коэффициенты разложения функции  .
.
Аналогично, приравнивая в (2.1.5) коэффициенты при  , найдем
, найдем
 (2.1.6)
(2.1.6)
Где Рk - полиномы от своих аргументов с положительными коэффициентами (у Р2 эти коэффициенты равны  ).
).
|
|
Таким образом, формальное решение (2.1.3) построено. Из единственности определения Сk следует, что если голоморфное решение задачи Коши (1.4) существует, то оно единственно.
Часть 2. Докажем теперь, что ряд (2.1.3) сходится в некоторой окрестности точки 0. Для этого достаточно построить степенной ряд, мажорирующий ряд (2.1.3), т.е. ряд
 (2.1.7)
(2.1.7)
С положительными коэффициентами, сходящийся в некоторой области
 (2.1.8)
(2.1.8)
И такой, что
 (2.1.9)
(2.1.9)
Тогда, как известно, ряд (2.1.3) будет заведомо сходиться в той же области (2.1.8)
Для построения ряда (2.1.7) рассмотрим мажорантную задачу Коши:
 (2.1.10)
(2.1.10)
Где  - некоторая мажоранта функции
- некоторая мажоранта функции  . В качестве
. В качестве  возьмем мажоранту Коши
возьмем мажоранту Коши

Где,  а M - сумма ряда
а M - сумма ряда
 (2.1.11)
(2.1.11)
(который сходится вследствие абсолютной сходимости ряда (2.1.2) в области  ), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2)
), Мажоранта F конструируется на основе оценки Коши коэффициента сходящегося степенного ряда (2.1.2)
 (2.1.12)
(2.1.12)
Вытекающей из (2.1.11).
Взяв ряд по степеням  и y с коэффициентом А тп, получим
и y с коэффициентом А тп, получим

Мажорантная задача Коши (2.1.10) примет вид
 (2.1.13)
(2.1.13)
Дифференциальное уравнение, входящее в задачу (2.1.13), называется мажорантным уравнением для уравнения задачи (1.4)
Мажорантная задача (2.1.13) имеет единственное решение. Найдём его.
Интегрируя мажорантное уравнение, имеем
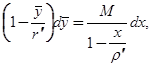 ,
,  (2.1.14)
(2.1.14)
Удовлетворяя начальному условию 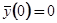 , найдем
, найдем  . Подставляя это значение С в (2.1.14) и умножая обе части на
. Подставляя это значение С в (2.1.14) и умножая обе части на  , получим
, получим
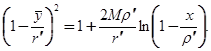
Разрешая относительно 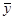 , найдем
, найдем
 (2.1.15)
(2.1.15)
Это решение голоморфно в точке 0 как суперпозиция двух голоморфных функций:

Таким образом, решение (2.1.15) представимо в виде
 (2.1.16)
(2.1.16)
Где ряд справа в некоторой окрестности точки 0 (по определению голоморфной функции). Оценим область сходимости ряда (2.1.16).
Согласно известной теореме Абеля достаточно ограничиться исследованием положительных значений  . Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения
. Так как радиус сходимости логарифмического и биномиального рядов равен 1, то допустимые значения  должны удовлетворять системе двух неравенств
должны удовлетворять системе двух неравенств
|
|
 (2.1.17)
(2.1.17)
Последнее неравенство следует из неравенства  с учётом того, что
с учётом того, что 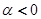
Решая второе из неравенств (2.1.17), имеем

Первое из неравенств (2.1.17) выполняется автоматически. Таким образом, ряд (2.1.16) сходится в области

Остается показать, что все коэффициенты ряда (2.1.16) положительны и что имеют место оценки (2.1.9).
Но это следует из того, что  можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим
можно найти методом неопределенных коэффициентов по тому же алгоритму, что и Сk. Получим
 (2.1.6 ‘)
(2.1.6 ‘)
Где Pk - те же самые полиномы, что и в (2.1.6), только аргументы другие: не коэффициенты разложения функции  , а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все
, а коэффициенты разложения мажоранты F. Из формулы (2.1.6 ‘) в силу положительности коэффициентов полиномов Pk и оценок (2.1.12) следует, что все  положительны и мажорируют Ck, т.е. имеют место оценки (2.1.9). Мажорирующий ряд (2.1.7) построен.
положительны и мажорируют Ck, т.е. имеют место оценки (2.1.9). Мажорирующий ряд (2.1.7) построен.
Таким образом, ряд (2.1.16) мажорирует формальное решение (2.1.3), чем завершается доказательство теоремы Коши.
|
|
|

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
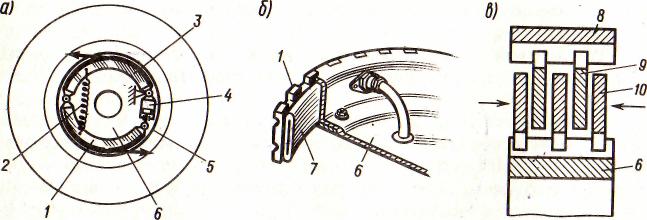
Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!