

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
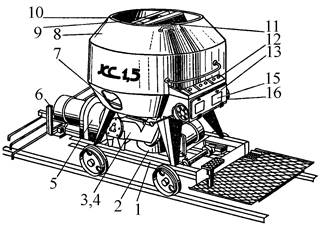
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пример 8.
Найти общее решение уравнения 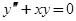 .
.
Ищем это решение в виде степенного ряда по степеням 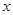 :
:
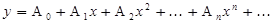
Формальным дифференцированием находим:
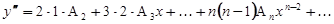
Подставляем в уравнение и приравниваем коэффициенты при одинаковых степенях 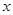 :
:
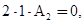
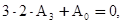
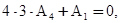
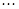
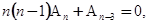
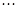
Из этих уравнений находим:
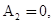
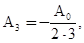
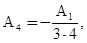
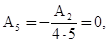
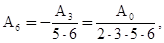
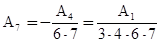
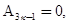
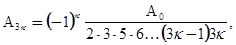
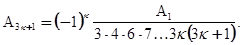
Коэффициенты 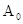 и
и 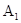 не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид:
не определяются этими уравнениями, это - два произвольных постоянных. Общее решение имеет вид:
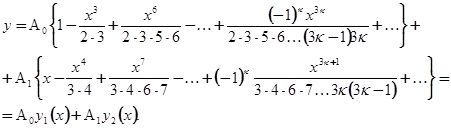
С помощью элементарных признаков легко установить сходимость рядов 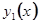 и
и 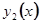 для всех значений
для всех значений 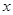 ; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси
; по общим свойствам степенных рядов эти ряды, так же как полученные из них формальным дифференцированием, сходятся равномерно на любом конечном отрезке оси 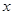 . Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.
. Следовательно, формальное получение этих решений оправдано, и они являются, в самом деле, решениями данного уравнения.
Метод интегрирования линейных дифференцированных уравнений рядами, расположенными по степеням 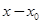 , применим также в некоторых случаях, когда коэффициент
, применим также в некоторых случаях, когда коэффициент 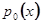 обращается в нуль при
обращается в нуль при 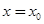 . Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени
. Однако получаемые при этом степенные ряды (сходящиеся) содержат, вообще говоря, не целые степени 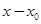 , а имеет вид:
, а имеет вид:
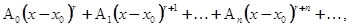 (5.1)
(5.1)
где r - некоторое число, вообще не целое. Уже из (5.1) ясно, что полное значение такого разложения может обнаружиться лишь при рассмотрении х как комплексного переменного, так как при 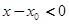 и дробном или иррациональном r выражение
и дробном или иррациональном r выражение 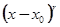 в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от
в действительной области может не иметь смысла. Теория Фукса дает условия, при которых уравнение n-го порядка имеет n частных решений вида (5.1) или еще более общего - произведения многочлена от 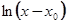 на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.
на ряд этого вида. Мы опять ограничимся рассмотрением одного случая, имеющего, однако, большой теоретический интерес, - так называемого гипергеометрического уравнения.
|
|
Рассмотрим уравнение вида:
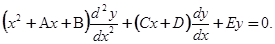 (5.2)
(5.2)
Корни многочлена второй степени, стоящего множителем при  , пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную
, пусть будут различны и действительны (однако ограничение отпадет, если рассматривать переменную 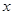 в комплексной области). Чтобы не вводить мнимых величин, мы предположим также, что А, В, C, D, E - действительные числа. В таком случае можно переписать уравнение (5.2) в виде:
в комплексной области). Чтобы не вводить мнимых величин, мы предположим также, что А, В, C, D, E - действительные числа. В таком случае можно переписать уравнение (5.2) в виде:
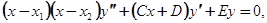 (5.2’)
(5.2’)
где 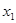 и
и 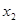 - корни многочлена
- корни многочлена 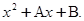 Это показывает, что коэффициент при
Это показывает, что коэффициент при 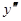 обращается в нуль при значениях
обращается в нуль при значениях 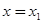 и
и 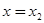 . Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с
. Преобразуем независимое переменное так, чтобы эти значения были 0 и 1. для этого вводим новое переменное z, связанное с 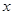 соотношением:
соотношением:
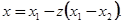
Тогда
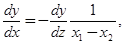
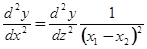 ,
,
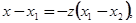
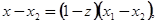
и мы получаем:
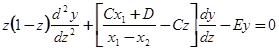 .
.
Вводя обозначения 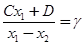 , C=α+β+1, E=αβ и обозначения независимое переменное снова через
, C=α+β+1, E=αβ и обозначения независимое переменное снова через 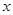 , мы получим гипергеометрическое уравнение в обычном его виде:
, мы получим гипергеометрическое уравнение в обычном его виде:
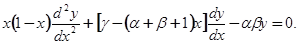 (5.3)
(5.3)
Пример 9.
Привести к виду (5.3) уравнение Лежандра 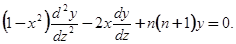 замена переменного
замена переменного 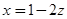 дает:
дает:
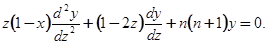
Здесь 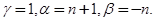
Мы видим, что уравнение (5.3) зависит от трех параметров: α, β, γ, причем параметры α и β входят симметрично. Найдем решения уравнения (5.3) в виде рядов по степеням 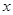 . подставляем в уравнение ряды:
. подставляем в уравнение ряды:
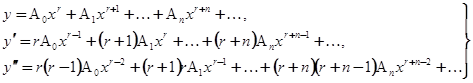 (5.4)
(5.4)
последний из рядов (5.4) умножаем на 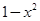 , второй ряд - на
, второй ряд - на 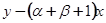 , третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях
, третий - на - αβ, складываем, собираем коэффициенты при одинаковых степенях 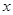 и приравниваем их к нулю. Низшая степень
и приравниваем их к нулю. Низшая степень 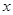 в результате будет
в результате будет 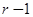 ; приравниваем нулю коэффициент при
; приравниваем нулю коэффициент при 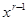 :
:
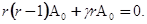
Без ограничения общности можно положить 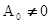 . тогда для r получается кратное уравнение:
. тогда для r получается кратное уравнение:
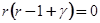 , откуда
, откуда 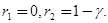
Исследуем решение, соответствующее значению 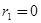 . Ряды (5.4) перепишутся так:
. Ряды (5.4) перепишутся так:
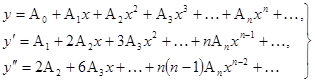 (5.4’)
(5.4’)
подстановка в уравнение (5.3) рядов (5.4’) дает свободный член в виде 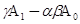 , откуда, предполагая γ≠0,
, откуда, предполагая γ≠0, 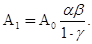
Собирая члены при 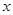 , получим:
, получим:
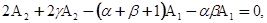
Или
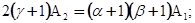
Следовательно (если γ≠-1),
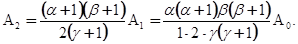
Вообще, члены, содержащие 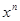 , дают:
, дают:
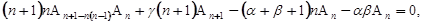
Откуда (если γ≠0, - 1, - 2,., - n)

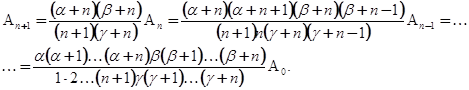
Полагая произвольное постоянное А0=1, получаем, в предложении, что γ не равно нулю или целому отрицательному числу, частное решение (5.3) - так называемый гипергеометрический ряд:
|
|
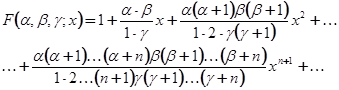 (5.5)
(5.5)
Признак сходимости Даламбера показывает, что ряд (5.5) сходится при 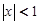 ; как известно из теории степенных рядов, он сходится равномерно в любом замкнутом интервале, внутреннем к (-1, +1), и допускает почленное дифференцирование любое число раз; следовательно, он удовлетворяет гипергеометрическому дифференциальному уравнению (5.3). Итак, первое частное решение уравнения (5.3) есть
; как известно из теории степенных рядов, он сходится равномерно в любом замкнутом интервале, внутреннем к (-1, +1), и допускает почленное дифференцирование любое число раз; следовательно, он удовлетворяет гипергеометрическому дифференциальному уравнению (5.3). Итак, первое частное решение уравнения (5.3) есть
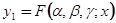
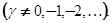
чтобы получить второе частное решение, можно было бы воспользоваться рядами (5.4), полагая в них 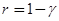 . Но мы скорее придем к цели, если в уравнение (5.3) введем новую функцию
. Но мы скорее придем к цели, если в уравнение (5.3) введем новую функцию 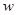 , связанную с y соотношением:
, связанную с y соотношением:
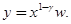
тогда
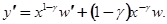
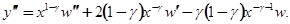
Подставляем в уравнение (5.3):
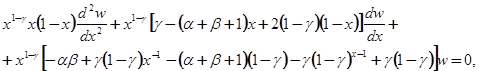
Или
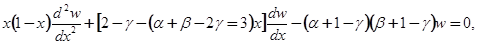
т.е. мы получили опять гипергеометрическое уравнение, в которое вместо параметров α, β, γ входят соответственно α+1-γ, β+1-γ, 2-γ.
Его решение в виде ряда, начинающегося с члена, не содержащего 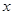 , есть F (α+1-γ, β+1-γ, 2-γ, х). Итак, второе частное решение уравнения (5.3) есть
, есть F (α+1-γ, β+1-γ, 2-γ, х). Итак, второе частное решение уравнения (5.3) есть
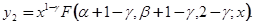
Оно имеет смысл, если 2-γ не равно нулю или целому отрицательному числу. В частности, оно имеет смысл всегда, когда γ равно нулю или целому отрицательному числу, т.е. когда теряет смысл y1. мы не останавливаемся на нахождении второго частного решения в указанных исключительных случаях.
Гипергеометрический ряд, содержащий три параметра,α, β, γ, дает при частных значениях этих параметров весьма большое число различных элементарных функций. Например, при α=γ получаем:
(α, β, γ; 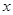 ) =
) = 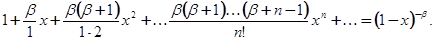
Далее, при 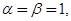
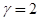 имеем
имеем
(1, 1, 2; 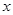 ) =
) = 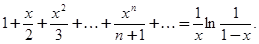
Заметим, наконец, что при α или β равном целому отрицательному числу-n, ряд (5.5) обрывается на члене, содержащем 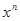 , т.е. является многочленом относительно
, т.е. является многочленом относительно 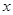 . так, например, при n целом одно решение уравнения Лежандра является многочленом; с точностью до постоянного множителя An этот так называемый многочлен Лежандра выражается так:
. так, например, при n целом одно решение уравнения Лежандра является многочленом; с точностью до постоянного множителя An этот так называемый многочлен Лежандра выражается так:
n (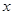 ) =
) = 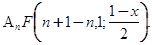
Метод, примененный нами для интегрирования гипергеометрического уравнения, применим к большому числу уравнений второго порядка, встречающегося в физике и механике. Так, например, для уравнения Бесселя:
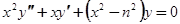
в случае если n не равно целому числу, он дает два ряда по возрастающим степеням 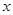 , начинающихся соответственно с
, начинающихся соответственно с 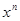 и
и 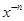 ; эти ряды определяют функции Бесселя
; эти ряды определяют функции Бесселя 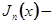 и
и 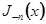 ; общее решение уравнения Бесселя есть
; общее решение уравнения Бесселя есть 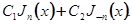
|
|
Если n равно целому числу (можно принять n≥0), то только одно частное решение выражается степенным рядом: 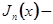 функция Бесселя первого рода; второе частное решение содержит еще 1
функция Бесселя первого рода; второе частное решение содержит еще 1 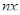 ; оно называется функцией Бесселя второго рода.
; оно называется функцией Бесселя второго рода.
Тот же способ без изменений может быть применен к нахождению решений уравнений порядка выше второго.
Уравнение Бесселя
В качестве примера приложения построенной теории рассмотрим уравнение Бесселя:
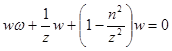 (6.1)
(6.1)
Где
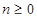 . Особая точка z =0 является регулярной. Других особенностей в конечной части плоскости нет.
. Особая точка z =0 является регулярной. Других особенностей в конечной части плоскости нет.
В уравнении (6.1) 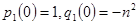 , поэтому определяющее уравнение имеет вид
, поэтому определяющее уравнение имеет вид
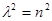 ,
,
Т.е. 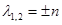 и
и 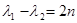 .
.
. Пусть 2n - не целое число.
Уравнение (6.1) имеет фундаментальную систему решений
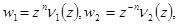
Где 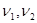 - целые функции, причём
- целые функции, причём 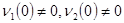 запишем
запишем 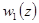 в виде обобщённого степенного ряда
в виде обобщённого степенного ряда
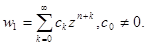 (6.2)
(6.2)
Дифференцируя (6.2) и подставляя выражения для 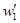 и
и 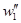 в уравнение (6.1), домноженное на
в уравнение (6.1), домноженное на 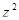 , получаем
, получаем
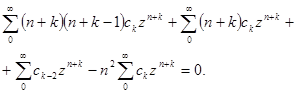 (6.3)
(6.3)
Сокращаем (6.3) на 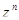 и приравниваем нулю коэффициент при
и приравниваем нулю коэффициент при 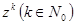 в левой части (6.3). Имеем:
в левой части (6.3). Имеем:
При 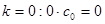 , следовательно, c0 произвольно, (6.4)
, следовательно, c0 произвольно, (6.4)
При 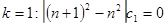 , следовательно, с1 =0; (6.5)
, следовательно, с1 =0; (6.5)
При 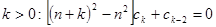 следовательно,
следовательно,
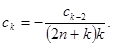 (6.6)
(6.6)
Формулы (6.4) - (6.6) позволяют последовательно определить все коэффициенты сk. При k нечётном сk=0.
Поскольку в рассматриваемом случае 2n - не целое число, коэффициенты обобщённого степенного ряда
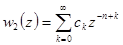 , (6.7)
, (6.7)
Также определяются по формулам (6.4) - (6.6), если в них заменить n на - n.. Пусть 2n - целое нечётное число: 2n=2p+1. коэффициенты ряда (6.2) определяются, как и в случае I, по формулам (6.4) - (6.6). Коэффициенты сk ряда (6.7) при k<2p+1 определяются по тем же формулам с заменой n на - n. Для определения с2p+1 получаем уравнение
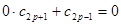 ,
,
Но так как по доказанному 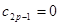 , то
, то 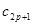 можно взять произвольным. Полагая
можно взять произвольным. Полагая 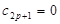 , остальные коэффициенты определяем по старым формулам, причём нечётные коэффициенты по-прежнему равны нулю. Таким образом, когда 2n нечётно, уравнение Бесселя не имеет решений, содержащих логарифм.б. Пусть 2n чётное: n=p. Коэффициенты ряда (6.2) определяются по старому правилу. При определении коэффициента ряда (6.7) встретится затруднение, так как он должен удовлетворять условию
, остальные коэффициенты определяем по старым формулам, причём нечётные коэффициенты по-прежнему равны нулю. Таким образом, когда 2n нечётно, уравнение Бесселя не имеет решений, содержащих логарифм.б. Пусть 2n чётное: n=p. Коэффициенты ряда (6.2) определяются по старому правилу. При определении коэффициента ряда (6.7) встретится затруднение, так как он должен удовлетворять условию
|
|
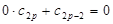 ,
,
не имеющему решений, так как
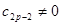 .
.
Это означает, что линейно независимого с 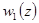 решения в виде обобщённого степенного ряда не существует. Из общей теории следует, что линейно независимое решение
решения в виде обобщённого степенного ряда не существует. Из общей теории следует, что линейно независимое решение 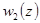 должно содержать логарифм.
должно содержать логарифм.
При определённом выборе произвольной постоянной с0 решения уравнения Бесселя, представляемые обобщёнными степенными рядами (6.2) и (6.7), называются функциями Бесселя первого рода. Они линейно независимы при 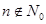 . Если же
. Если же 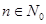 , то линейно независимое с (6.2) решение, содержащее логарифм, называется при определённом выборе произвольной постоянной функцией Бесселя второго рода.
, то линейно независимое с (6.2) решение, содержащее логарифм, называется при определённом выборе произвольной постоянной функцией Бесселя второго рода.
Заключение
Во всех рассмотренных случаях в первом пункте голоморфные решения задачи Коши представимы рядами Тейлора.
Следует иметь в виду, что всегда представляется весьма перспективным иметь голоморфное решение задачи Коши, которое является источником приближенных решений. Здесь степенной ряд выступает как поисковый аналитический аппарат, представляющий собой решение задачи Коши. Получающиеся при этом степенные ряды, как правило, не суммируются, т.е. их суммы не являются элементарными функциями, так что в этом случае дифференциальные уравнения являются источником новых элементарных функций.
Иногда степенные ряды, представляющие голоморфные решения дифференциальных уравнений, обрываются, обращаясь в полиномы.
Рассмотренный способ интегрирования дифференциальных уравнений распространяется и на системе дифференциальных уравнений с опорой на теорему Коши. Наиболее успешно он применяется к интегрированию однородных линейных систем, для чего, так же как и в случае однородного линейного уравнения, достаточно построить фундаментальную систему решений, голоморфную в некоторой точке голоморфности коэффициентов системы (обычно строят фундаментальную систему решений, нормированную в этой точке).
|
|
|

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
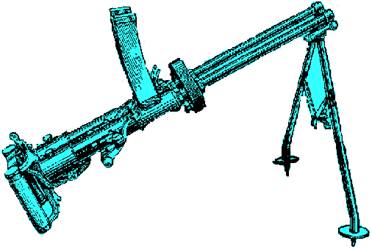
История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
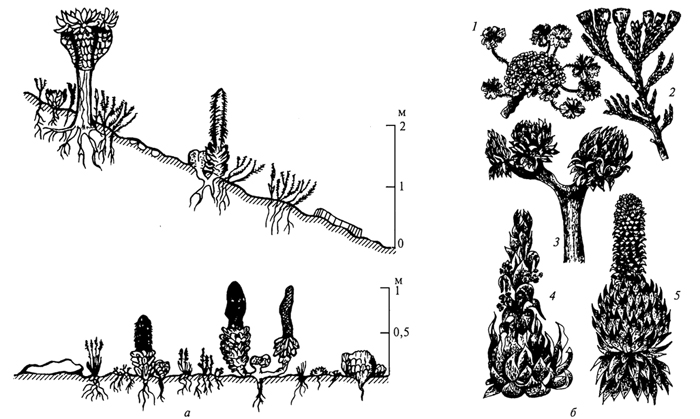
Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!