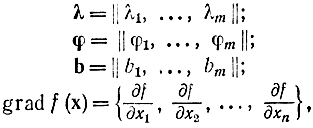Теорема Куна-Таккера является обобщением методов решения оптимизационных задач в двух направлениях:
- линейного программирования на нелинейный случай, который получил по аналогии не очень удачное название «нелинейного программирования»;
- нелинейных ограничений равенств на ограничения неравенства.
Метод и условия Каруша-Куна-Таккера (Karush-Kuhn- Tucker conditions, KKT) формально являются необходимыми условиями оптимальности задачи нелинейного программирования. Кроме того, необходимые условия включают, так называемые условия регулярности стационарных точек – невырожденность множества градиентов ограничений. Метод является обобщением метода множителей Лагранжа на случай ограничений неравенств.
Кун и Таккер обобщили метод множителей Лагранжа (для использования при построении критериев оптимальности для задач с ограничениями в виде равенств) на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств 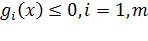 .
.
Основным методом в нелинейном программировании до сих пор остаётся применение функции Лагранжа, полученной переносом ограничений в целевую функцию. Условия Куна-Таккера также выведены из этого принципа.
Вильям Каруш в своей дипломной работе в 1931 году нашёл необходимые условия в общем случае ограничений равенств и неравенств. Независимо от него к тем же выводам позднее в 1941 году пришли Гарольд Кун и Альберт Таккер. Полученные ими результаты были более общими.
Если  при наложенных ограничениях является решением задачи, то найдётся вектор множителей Лагранжа
при наложенных ограничениях является решением задачи, то найдётся вектор множителей Лагранжа  такой, что для функции Лагранжа
такой, что для функции Лагранжа  выполняются условия:
выполняются условия:
- стационарности: 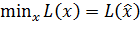 ;
;
- дополняющей нежёсткости: 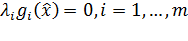 ;
;
- неотрицательности:. 
Перечисленные необходимые условия минимума функции в общем случае не являются достаточными. Существует несколько вариантов дополнительных условий, которые делают их достаточными:
- простое условие – 1) точка 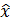 стационарна, 2)выполняется условие дополняющей нежесткости, 3) множители Лагранжа
стационарна, 2)выполняется условие дополняющей нежесткости, 3) множители Лагранжа  ;
;
- условие Слейтера (более слабое) – 1) точка 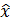 стационарна, 2) выполняется условие дополняющей нежесткости, 3)
стационарна, 2) выполняется условие дополняющей нежесткости, 3) 
 .
.
Перейдём непосредственно к доказательству теоремы Куна-Таккера.
Если непрерывная функция n переменных x = (x1,...,xn) F(х) имеет в точке х оптмаксимум, то существует ε > 0 такое, что для всех x из ε-окрестности точки х опт
F(x)≤F(xопт)
или
F(x)-F(xопт)≤0.
Выберем два вида приращения xj вдоль j -й координаты
Δxj=xj-xjопт>0,
Δxj=xj-xjопт<0.
Тогда

Переходя в этих соотношениях к пределу при Δ xj →0, получаем:

Из этих соотношений следует, что
 (3.6.1)
(3.6.1)
Аналогичное соотношение можно получить для случая минимума функции. Таким образом, доказана необходимость условий (3.6.1) для достижения в точке хопт максимума или минимума функции f(х), т. е. если имеется экстремум, то условия (3.6.1) удовлетворяются. Но равенство нулю всех производных в точке хопт еще не обеспечивает существования в ней экстремума, т. е. условия (3.6.1) не являются достаточными. Геометрически это означает, что в случае нулевой производной от функции одной переменной может иметь место точка перегиба, а не максимум (или минимум), а в случае функции двух переменных - седловая точка, а не экстремум и т. д. Поэтому точки хопт, в которых выполняются соотношения (3.6.1), называются стационарными.
Заметим, что условие (3.6.1) удалось получить благодаря возможности придавать переменной х приращения двух знаков, откуда и возникли два неравенства при 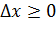 и при
и при  . Если допустимая область значений х ограничена неотрицательными значениями х ≥0, то внутри области, где х > 0, справедливость условия (3.6.1) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δ х >0, можно говорить только об односторонней производной, и из (3.6.1) следует следующее необходимое условие максимума:
. Если допустимая область значений х ограничена неотрицательными значениями х ≥0, то внутри области, где х > 0, справедливость условия (3.6.1) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δ х >0, можно говорить только об односторонней производной, и из (3.6.1) следует следующее необходимое условие максимума:

Соответственно, необходимое условие минимума на границе области хj = 0 запишется в виде
 .
.
б) Задача на условный экстремум
При определении условного экстремума функции, когда требуется определить максимум (или минимум) функции F(х) при ограничивающих условиях:
gi(x) = bi, i = 1,..., m,
т. е.
f(x)=max;
gi(x)=bi;
используется также метод множителей Лагранжа, который, так же как в случае классического вариационного исчисления, заключается во введении функции Лагранжа
 (3.6.2)
(3.6.2)
где λi - неопределенные множители Лагранжа.
Полагая, что функция является частным случаем функционала, получаем, что необходимые условия экстремума находятся прямым дифференцированием соотношения (3.6.2) и записываются в виде

Если ввести в рассмотрение векторы
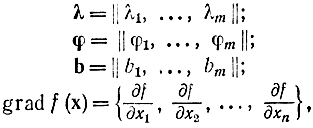
соотношения (17-8) и (17-9) перепишутся как
grad Φ = grad F - λ grad φ = 0; (3.6.6)
b - φ = 0,
где равенство нулю векторов понимается покомпонентно.
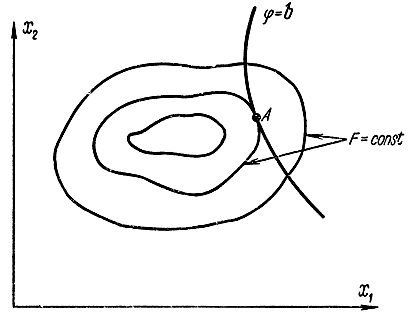
Рисунок 3.6.1 - Пояснение к задаче на условный экстремум
В случае n = 2 и m = 1 геометрическая задача об отыскании условного экстремума сводится (рис. 17-6) к отысканию точки касания А кривой φ = b к одной из кривых постоянного уровня f = const.





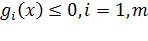 .
. при наложенных ограничениях является решением задачи, то найдётся вектор множителей Лагранжа
при наложенных ограничениях является решением задачи, то найдётся вектор множителей Лагранжа  такой, что для функции Лагранжа
такой, что для функции Лагранжа  выполняются условия:
выполняются условия: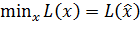 ;
;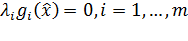 ;
;
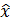 стационарна, 2)выполняется условие дополняющей нежесткости, 3) множители Лагранжа
стационарна, 2)выполняется условие дополняющей нежесткости, 3) множители Лагранжа  ;
;
 .
.

 (3.6.1)
(3.6.1)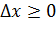 и при
и при  . Если допустимая область значений х ограничена неотрицательными значениями х ≥0, то внутри области, где х > 0, справедливость условия (3.6.1) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δ х >0, можно говорить только об односторонней производной, и из (3.6.1) следует следующее необходимое условие максимума:
. Если допустимая область значений х ограничена неотрицательными значениями х ≥0, то внутри области, где х > 0, справедливость условия (3.6.1) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ≥ 0, где х = 0, допускается только положительное приращение Δ х >0, можно говорить только об односторонней производной, и из (3.6.1) следует следующее необходимое условие максимума:
 .
.