Как это не выглядит странно, но первые задачи по оптимизации не являлись самыми простыми задачами по нахождению минимумов и максимумов обычных функций нескольких переменных  :
:
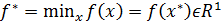 .
.
Они относятся к классу конечномерных задач, так как аргумент, состоящий из n вещественных чисел, является вектором конечномерного пространства. Кроме того, в её простейшем варианте, отсутствуют дополнительные условия, которые можно задавать равенствами или неравенствами для других функций, которые называют ограничениями.
А именно, ещё в древней Греции была решена более сложная, связанная с именами Евклида, Архимеда и Аристотеля изопериметрическая задача Дидоны на нахождение фигуры на плоскости с максимальной площадью при заданном периметре. Она относилась к бесконечномерным задачам, так как аргументом являлась функция, т.е. объект, который зависит от бесконечного числа переменных, а оптимизировался определённый интеграл, являющийся функционалом на пространстве функций. Эта задача относиться к вариационным задачам с ограничениями, а не к поиску экстремума функций без ограничений.
Следующим важным моментом развития в районе 1650 года явилась теорема Ферма о том, что в экстремальных точках называемый градиентом вектор частных производных функции равен 0. После этого и ещё до решения задачи нахождения экстремума функции при наличии ограничений Иоганн Бернулли в 1699 году поставил, а затем и получил решение этапной задачи о брахистохроне: кривой, по которой материальная точка в поле силы тяжести спуститься из одной точки в другую, более низкую, точку, за минимальное время. Решение было получено очень быстро, за 1-2-года, и не только Бернулли, но и ещё Эйлером, Лейбницем и анонимным автором, оказавшимся Ньютоном.
Решая эту и подобные вариационные задачи, Эйлер получил обыкновенные дифференциальные уравнения, названные позднее уравнениями Эйлера, которым должно удовлетворять решение. Напомним, что более простые конечномерные задачи поиска экстремума функций имели аргументом конечномерный вектор в  . Вариационные задачи связаны с оптимизацией интегралов, имеют аргументами функции, которые, вообще говоря, являются бесконечномерными объектами, определёнными на континууме. Поэтому вариационные задачи относят к бесконечномерной оптимизации, которые в целом, значительно сложнее конечномерной.
. Вариационные задачи связаны с оптимизацией интегралов, имеют аргументами функции, которые, вообще говоря, являются бесконечномерными объектами, определёнными на континууме. Поэтому вариационные задачи относят к бесконечномерной оптимизации, которые в целом, значительно сложнее конечномерной.
Однако вначале учёные занимались вариационными задачами. Правда, метод исследования был основан на рассмотрении конечномерных объектов. А именно, Эйлер заменял интегралы на интегральные суммы, которые уже зависели от конечного числа точек-аргументов, и соответствующая экстремальная задача была уже конечномерной.
Так, для изопериметрической задачи произвольная кривая на плоскости приближалась ломаными, образующими треугольники и многоугольники. И сначала решение искалось для этих многоугольников, которые в пределе давали уравнения Эйлера и соответствующее решение.
Эталонная вариационная задача состоит в минимизации интеграла

среди всех кривых C: 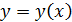 , соединяющих две заданные точки.
, соединяющих две заданные точки.
Для параметрических кривых  интеграл соответственно модифицируется
интеграл соответственно модифицируется
 ,
,
при этом должно выполняться условие однородности, унифицирующее параметрическое представление
 ,
,  .
.





 :
: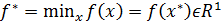 .
. . Вариационные задачи связаны с оптимизацией интегралов, имеют аргументами функции, которые, вообще говоря, являются бесконечномерными объектами, определёнными на континууме. Поэтому вариационные задачи относят к бесконечномерной оптимизации, которые в целом, значительно сложнее конечномерной.
. Вариационные задачи связаны с оптимизацией интегралов, имеют аргументами функции, которые, вообще говоря, являются бесконечномерными объектами, определёнными на континууме. Поэтому вариационные задачи относят к бесконечномерной оптимизации, которые в целом, значительно сложнее конечномерной.
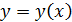 , соединяющих две заданные точки.
, соединяющих две заданные точки. интеграл соответственно модифицируется
интеграл соответственно модифицируется ,
, ,
,  .
.

