Определение коэффициента гидравлического сопротивления внутренней поверхности трубопровода

 

Потери напора по длине для труб постоянного диаметра определяются по формуле Дарси-Вейсбаха

(1)

где l — коэффициент гидравлического сопротивления (гидравлического трения); l — длина трубы; d — ее внутренний диаметр; u — средняя скорость потока.

Входящий в нее коэффициент гидравлического сопротивления и является функцией числа Рейнольдса Rе и относительной шероховатости

где 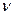—кинематическая вязкость, перекачиваемой нефти, Q — объемный расход, е — абсолютная шероховатость стенок трубопровода.

При ламинарном течении, а также и при турбулентном в зоне сравнительно небольших Rе, выступы шероховатости плавно обтекаются потоком жидкости, шероховатость не влияет на потерю напора и коэффициент гидравлического сопротивления зависит только от числа Рейнольдса. С увеличением Rе коэффициент уменьшается.

Область, в которой называется областью гладкого трения.

Увеличение числа Рейнольдса приводит к тому, что от бугорков шероховатости начинают отрываться вихри. Это явление наступает тем раньше, чем больше шероховатость. Теперь сопротивление течению жидкости зависит не только от числа Рейнольдса, но и от шероховатости.

Область, в которой называется областью смешанного трения. Здесь с увеличением Rе его влияние на постепенно уменьшается, а влияние — возрастает (увеличивается интенсивность вихреобразования у выступов шероховатости).

При больших числа Рейнольдса коэффициент , перестает зависеть от Rе.

Область, в которой , называется областью совершенно шероховатого трения или областью квадратичного режима движения, так как здесь — постоянная величина и потеря напора прямо пропорциональна квадрату скорости.

При ламинарном течении (Rе < 2000) коэффициент гидравлического сопротивления находят то формуле Стокса:

Ламинарный режим бывает при перекачке вязких нефтей. Для вычисления при турбулентном режиме (Rе > 3000) в зоне гладкого трения служит эмпирическая формула Блазиуса:

Обычно этой формулой пользуются при расчете нефтепроводов для нефти средней вязкости.

В зоне квадратичного закона трения коэффициент гидравлического сопротивления определяется по формуле Никурадзе:

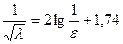
Альтшуль рекомендует пользоваться формулой Шифринсона:

где К — эквивалентная шероховатость, характеризующая суммарное влияние состояния внутренней поверхности стенки трубопровода на гидравлическое сопротивление.

В формуле Никурадзе и во всех остальных приведенных ниже формулах величину также следует определять по эквивалентной шероховатости

Квадратичного режима в нефтепроводах не бывает. Лишь приближенно иногда считают, что при квадратичном режиме могут перекачиваться светлые нефтепродукты. Квадратичный закон трения может быть в магистральных газопроводах.

Для определения коэффициента гидравлического сопротивления в зоне смешанного трения применяются «универсальные» формулы. Их структура такова, что при малых числах Рейнольдса они обращаются в формулы ,а при больших — переходят в формулы . Впервые такого типа формула была предложена Кольбруком и Уайтом:

.

Если, здесь пренебречь стоящим в скобках вторым членом, то останется формула Никурадзе для квадратичного закона трения.

Если же пренебречь первым членом получим формулу Прандтля для режима гладкого трения:

.

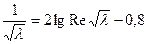Результаты вычислений по формуле Кольбрука и Уайта хорошо совпадают с опытными данными, полученными на технических трубопроводах. Но эта формула имеет существенный недостаток: при вычислении необходимо прибегать к методу последовательных приближений.

От этого недостатка свободны аналогичные формулы (дающие практически такие же результаты), предложенные Френкелем

,

Исаевым

Особой простотой отличается формула Альтшуля

.

При она практически совпадает с формулой Блазиуса, а при — с формулой Шифринсона; можно считать границей между областями гладкого и смешанного трения, — границей между областями смешанного и совершенно шероховатого трения.

 

Обобщенная формула Лейбензона

 

Формулы Стокса, Блазиуса и Никурадзе (а также и Шифринсона) имеют следующий общий вид:

, (2)

где А и т — постоянные величины, т называется показателем режима движения жидкости.

Подставив (6) в уравнение Дарси-Вейсбаха (5) и учитывая 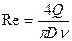, получим обобщенную формулу Лейбензона:

,

где

.

Формула Лейбензона широко применяется в тех случаях, когда зависимость от Q должна быть выражена в явном виде. Величины т, А и имеют следующие значения:

	т	А	, сек2/м:
Ламинарный режим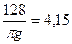
Турбулентный режим в зоне Блазиуса	0,25	0,3164
Область квадратичного закона трения

 

На графике зависимость (2) для указанных в таблице режимов течения выглядит в виде прямых линий, тангенс угла наклона которых к оси lgRe равен т. В области смешанного трения, где зависит не только от Rе, но и от относительной шероховатости , линия оказывается плавной кривой. Показатель режима течения т в этой области — переменная величина.

Последнее обстоятельство исключает возможность использования формулы Лейбензона в области смешанного трения. Это большой недостаток, так как область смешанного трения охватывает широкий интервал чисел Рейнольдса, при которых обычно ведутся перекачки маловязких нефтей и светлых нефтепродуктов. Однако ценой некоторой потери в точности расчетов этот недостаток может быть устранен.

Отметим на графике (рис. 1) цифрой 1 точку на прямой Блазиуcа, где , и цифрой 2 точку на прямой Шифринсона, где (границы области смешанного трения). Подставив Re1 в формулу Блазиуеа, а Re2 в формулу Шифринсона, найдем и — ординаты точек 1 и 2.

Теперь проведем через точки 1-й 2 прямую. Ее уравнение приводится к виду

.

Приняв

,

получим

. (3)

Очевидно, замена кривой прямой 1—2 равносильна замене формулы Альтшуля формулой (7). Это дает возможность распространить формулу Лейбензона и на область смешанного трения. Для этой области в соответствии с (3) т =0,123. Коэффициент будет зависеть от (так как от зависит А). Но это не вызовет существенных неудобств при практических расчетах: величину при заданном значении можно найти в таблице, полученной на основании приведенных выше формул.

Рис. 1. Замена Кривой прямой линией