Ряды Фурье. Интеграл Фурье. Операционное исчисление
Учебно-методическое пособие
САНКТ-ПЕТЕРБУРГ
2005
УДК 512 + 517.2 (075.80)
ББК 22.161.5
Г723
Учебно-методическое пособие дает возможность получить практические навыки анализа функций с помощью разложения в ряд Фурье или представления интегралом Фурье и предназначено для самостоятельной работы студентов дневной и заочной форм обучения специальностей.
В пособии рассмотрены основные вопросы операционного исчисления и широкий класс технических задач с применением основ операционного исчисления.
Научный редактор проф. А.П. Господариков
Рецензенты: кафедра высшей математики № 1 Санкт-Петербургского государственного электротехнического университета; доктор физ.-мат. наук В.М. Чистяков (Санкт-Петербургский государственный политехнический университет).
Господариков А.П.
Г723. Ряды Фурье. Интеграл Фурье. Операционное исчисление: Учебно-методическое пособие / А.П. Господариков, Г.А. Колтон, С.А. Хачатрян; Санкт-Петербургский государственный горный институт (технический университет). СПб, 2005. 102 с.
ISBN 5-94211-104-9
УДК 512 + 517.2 (075.80)
ББК 22.161.5
Введение
Из теории Фурье известно, что при некотором воздействии на физические, технические и другие системы, его результат повторяет форму начального входного сигнала, отличаясь только масштабным коэффициентом. Понятно, что на такие сигналы (их называют собственными) система реагирует наиболее простым образом. Если произвольный входной сигнал есть линейная комбинация собственных сигналов, а система линейна, то реакция системы на этот произвольный сигнал есть сумма реакций на собственные сигналы. И поэтому полную информацию о системе можно получить по «кирпичикам» – откликам системы на собственные входные сигналы. Так поступают, например, в электротехнике, когда вводят частотную характеристику системы (передаточную функцию). Для наиболее простых линейных, инвариантных во времени систем (например, описываемых обыкновенными дифференциальными уравнениями с постоянными коэффициентами) в некоторых случаях собственными функциями являются гармоники вида  . Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье.
. Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье.
Глава 1. Ряды Фурье
Векторные пространства
Здесь приведены краткие сведения из векторной алгебры, необходимые для лучшего понимания основных положений теории рядов Фурье.
Рассмотрим множество W геометрических векторов (векторное пространство), для которого обычным образом введены понятие равенства векторов, линейные операции (сложение и вычитание векторов, умножение вектора на число) и операции скалярного умножения векторов.
Введем в пространстве W ортогональный базис, состоящий из трех попарно ортогональных векторов  ,
,  и
и 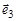 . Произвольный вектор
. Произвольный вектор  является линейной комбинацией векторов базиса:
является линейной комбинацией векторов базиса:
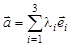 . (1.1)
. (1.1)
Коэффициенты l i (i = 1, 2, 3), называемые координатами вектора 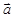 относительно базиса
относительно базиса  , могут быть определены следующим образом. Скалярное произведение вектора
, могут быть определены следующим образом. Скалярное произведение вектора 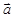 и одного из векторов базиса
и одного из векторов базиса 
 .
.
В силу ортогональности базиса скалярные произведения  при
при  , следовательно, в правой части последнего равенства отлично от нуля лишь одно слагаемое, соответствующее
, следовательно, в правой части последнего равенства отлично от нуля лишь одно слагаемое, соответствующее  , поэтому
, поэтому  , откуда
, откуда
 , (1.2)
, (1.2)
где  .
.
Если векторы  и
и  заданы своими координатами
заданы своими координатами  и
и  , то их скалярное произведение
, то их скалярное произведение
 .
.
Так как при 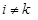 скалярное произведение
скалярное произведение  , то в двойной сумме отличны от нуля лишь слагаемые с равными индексами, поэтому
, то в двойной сумме отличны от нуля лишь слагаемые с равными индексами, поэтому
 . (1.3)
. (1.3)
В частности при  из (1.3) следует
из (1.3) следует
 . (1.4)
. (1.4)
Глава 2. Интеграл Фурье
Сходимость интеграла Фурье
Пусть функция  определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
 , (11.1)
, (11.1)
где
 ; (11.2)
; (11.2)
 – частота k -й гармоники;
– частота k -й гармоники; 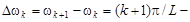
 .
.
Введя в (11.1) выражения (11.2), получим
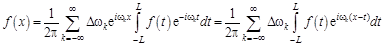 . (11.3)
. (11.3)
При 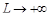 величина
величина 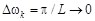 . Правая часть формулы (11.3) аналогична интегральной сумме для функции
. Правая часть формулы (11.3) аналогична интегральной сумме для функции  по переменной w в промежутке
по переменной w в промежутке  . Поэтому можно ожидать, что после перехода в (11.3) к пределу при
. Поэтому можно ожидать, что после перехода в (11.3) к пределу при  вместо ряда получим интеграл
вместо ряда получим интеграл
 . (11.4)
. (11.4)
Формула (11.4) называется интегральной формулой Фурье, а ее правая часть – интегралом Фурье.
Рассуждения, с помощью которых получена формула (11.4), не являются строгими и имеют лишь наводящий характер. Условия, при которых справедлива интегральная формула Фурье, устанавливает теорема, принимаемая нами без доказательства.
Теорема. Пусть функция  , во-первых, абсолютно интегрируема на промежутке
, во-первых, абсолютно интегрируема на промежутке  , т.е. интеграл
, т.е. интеграл  сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к
сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к  , т.е. равенство (11.4) выполняется при всех х из промежутка
, т.е. равенство (11.4) выполняется при всех х из промежутка  . Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
. Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
§ 12. Преобразование Фурье
Интегральную формулу Фурье (11.4) преобразуем следующим образом. Положим
 . (12.1)
. (12.1)
Если функция  непрерывна и абсолютно интегрируема на всей оси, то функция
непрерывна и абсолютно интегрируема на всей оси, то функция  непрерывна на промежутке
непрерывна на промежутке  . Действительно, так как
. Действительно, так как  , то
, то
 , (12.2)
, (12.2)
и, поскольку интеграл справа сходится, то сходится интеграл слева. следовательно, интеграл в (12.1) сходится абсолютно. Равенство (12.2) выполняется одновременно для всех 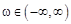 , поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция
, поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция  непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
Из (11.4) получим
 . (12.3)
. (12.3)
Комплексная функция  , определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции
, определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции  . В свою очередь, формула (12.3) определяет
. В свою очередь, формула (12.3) определяет  как обратное преобразование Фурье, или прообраз функции
как обратное преобразование Фурье, или прообраз функции  . Равенство (12.3) при заданной функции
. Равенство (12.3) при заданной функции  можно рассматривать, как интегральное уравнение относительно функции
можно рассматривать, как интегральное уравнение относительно функции  , решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции
, решение которого дается формулой (12.1). И, наоборот, решение интегрального уравнения (12.1) относительно функции  при заданной
при заданной  дает формула (12.3).
дает формула (12.3).
В формуле (12.3) выражение  задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке
задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке  и суммарной комплексной амплитудой
и суммарной комплексной амплитудой  . Функция
. Функция 
 называется спектральной плотностью. Формулу (12.2), записанную в виде
называется спектральной плотностью. Формулу (12.2), записанную в виде
 ,
,
можно трактовать, как разложение функции  в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке
в сумму пакетов гармоник, частоты которых образуют сплошной спектр, распределенный на промежутке  .
.
Равенства Парсеваля. Пусть  и
и  – Фурье-образы вещественных функций
– Фурье-образы вещественных функций  и
и  соответственно. Тогда
соответственно. Тогда
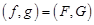 ; (12.4)
; (12.4)
 , (12.5)
, (12.5)
т.е. скалярные произведения и нормы функций являются инвариантами преобразования Фурье. Докажем это утверждение. по определению скалярного произведения имеем  . Заменив функцию
. Заменив функцию 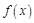 ее выражением (12.3) через Фурье-образ
ее выражением (12.3) через Фурье-образ  , получим
, получим
 .
.
В силу (12.1)
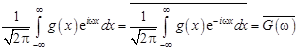 .
.
Поэтому  , т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при
, т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при  .
.
Косинус- и синус-преобразования Фурье. Если вещественная функция  четна, то ее Фурье-образ, который здесь будем обозначать
четна, то ее Фурье-образ, который здесь будем обозначать  , также является вещественной четной функцией. Действительно,
, также является вещественной четной функцией. Действительно,


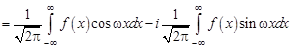 .
.
Последний интеграл, вследствие нечетности подынтегральной функции, обращается в нуль. Таким образом,
 . (12.6)
. (12.6)
Здесь использовано свойство (7.1) четных функций.
Из (12.6) следует, что функция  вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
вещественна и четным образом зависит от w, так как w входит в (12.6) только через косинус.
Формула (12.3) обратного преобразования Фурье в этом случае дает

=  .
.
Так как  и
и  – соответственно четная и нечетная функции переменной w, то
– соответственно четная и нечетная функции переменной w, то
 . (12.7)
. (12.7)
Формулы (12.6) и (12.7) определяют косинус-преобразование Фурье.
Аналогично, если вещественная функция 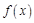 нечетна, то ее преобразование Фурье
нечетна, то ее преобразование Фурье  , где
, где  – вещественная нечетная функция от w. При этом
– вещественная нечетная функция от w. При этом
 ; (12.8)
; (12.8)
 . (12.9)
. (12.9)
Равенства (12.8), (12.9) задают синус-преобразование Фурье.
Заметим, что в формулы (12.6) и (12.8) входят значения функции  только для
только для  . Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке
. Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке  . В этом случае при
. В этом случае при  интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при
интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при  к ее четному и нечетному продолжениям соответственно.
к ее четному и нечетному продолжениям соответственно.
Покажем, как с помощью преобразования Фурье вычисляются некоторые несобственные «неберущиеся» интегралы.
Пример 1. Вычислить интеграл Лапласа  .
.
Решение. Найдем Фурье-образ функции  где
где  :
:
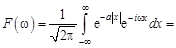


 .
.
С помощью формулы обратного преобразования Фурье

получим

или
 .
.
Здесь первое слагаемое представляет собой удвоенный интеграл Лапласа, а второе равно нулю вследствие нечетности подынтегральной функции. Поэтому
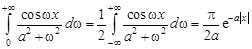 .
.
Пример 2. Вычислить разрывной множитель Дирихле  , если
, если  .
.
Решение. Применив косинус-преобразование Фурье к четной функции

получим
 ;
;
 .
.
Таким образом,

В частности интеграл Дирихле
 .
.
Пример 3. Вычислить интеграл Эйлера-Пуассона 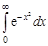 .
.
Решение. Сначала вычислим интеграл  , применив к функции
, применив к функции 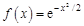 , где
, где  , преобразование Фурье и введя замену
, преобразование Фурье и введя замену 

=  ;
;

 .
.
Отсюда  , и, следовательно, с заменой
, и, следовательно, с заменой 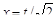 можно записать
можно записать
 .
.
Упражнение 1. Используя равенство Парсеваля, вычислить интегралы
 ;
;  .
.
Упражнение 2. Доказать, что
 ,
,
используя равенство Парсеваля.
§ 13. Основные сведения из теории преобразования Фурье
Тот факт, что функция  является Фурье-образом функции
является Фурье-образом функции  , будем обозначать в дальнейшем одним из следующих способов:
, будем обозначать в дальнейшем одним из следующих способов: 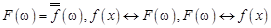 .
.
Свойства преобразования Фурье:
1. Теорема линейности. 
 , где
, где  . Это свойство сразу следует из определения (12.1) и линейности операции интегрирования.
. Это свойство сразу следует из определения (12.1) и линейности операции интегрирования.
2. Теорема подобия.  , где
, где  . Обозначив
. Обозначив  , получим
, получим

3. Теорема смещения.  , где
, где 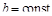 . Введя замену
. Введя замену  , получим
, получим
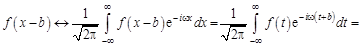
 .
.
Следствие.
 , (13.1)
, (13.1)
где  . Действительно,
. Действительно,

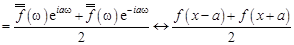 .
.
4. Теорема о свертке. Напомним, что сверткой абсолютно интегрируемых функций  и
и  называется функция
называется функция
 .
.
Фурье-образ свертки функций f и g равен произведению их Фурье-образов, умноженному на  :
:  .
.
Так как по определению


 ,
,
то, выполнив во внутреннем интеграле замену  , получим
, получим

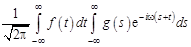 =
=
= 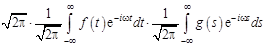 =
=  ,
,
что и требовалось доказать.
5. Теорема об образе производной. Пусть функция  и ее производная
и ее производная  абсолютно интегрируемы на промежутке
абсолютно интегрируемы на промежутке  . По формуле Ньютона – Лейбница
. По формуле Ньютона – Лейбница
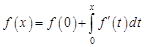 .
.
Так как производная 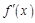 интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при
интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при  . Следовательно, существует конечный предел
. Следовательно, существует конечный предел 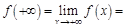
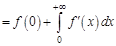 . При этом
. При этом  , ибо в противном случае функция
, ибо в противном случае функция 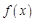 была бы неинтегрируемой на промежутке
была бы неинтегрируемой на промежутке 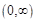 . Точно также доказывается, что
. Точно также доказывается, что  .
.
Введем в рассмотрение Фурье-образ производной
 .
.
Выполнив интегрирование по частям, получим
 .
.
Так как внеинтегральный член равен нулю, то
 .
.
Таким образом, операции дифференцирования функции  соответствует операция умножения ее Фурье-образа на множитель
соответствует операция умножения ее Фурье-образа на множитель  . Аналогично, если функция
. Аналогично, если функция  имеет абсолютно интегрируемые производные до n- го порядка включительно, то
имеет абсолютно интегрируемые производные до n- го порядка включительно, то

 ,
,  .
.
Следствия. 1. Обыкновенное линейное дифференциальное уравнение с постоянными коэффициентами преобразованием Фурье переводится в линейное алгебраическое уравнение.
2. Линейное уравнение в частных производных с постоянными коэффициентами и с двумя независимыми переменными преобразованием Фурье по одной из переменных переводится в обыкновенное линейное дифференциальное уравнение.
Пример 1. Доказать, что
 , (13.2)
, (13.2)
где  .
.
Решение. Положим

Тогда
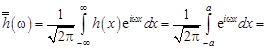

Таким образом,
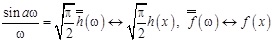 ,
,
и по теореме о свертке

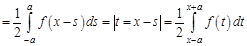 .
.
Пример 2. Найти решение уравнения
 (13.3)
(13.3)
при  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию
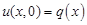 . (13.4)
. (13.4)
Замечание. Уравнение (13.3) называется уравнением теплопроводности. Уравнениями такого вида описываются одномерные процессы диффузии, переноса тепла и т.п.
Решение. Применим к уравнению (13.3) преобразование Фурье. Для этого, умножив обе части уравнения на  , проинтегрируем его по х от
, проинтегрируем его по х от  до
до  . Тогда
. Тогда

или
 , (13.5)
, (13.5)
где 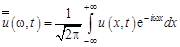 – Фурье-образ функции
– Фурье-образ функции  .
.
Здесь использовалась формула для Фурье-образа производной второго порядка:
 .
.
Равенство (13.5) – это обыкновенное линейное дифференциальное уравнение первого порядка относительно функции  переменной t, где w – параметр.
переменной t, где w – параметр.
Переходя к Фурье-образам в равенстве (13.4), получим начальное условие для уравнения (13.5):
 . (13.6)
. (13.6)
Решением задачи Коши (13.5), (13.6) является функция
 .
.
С помощью (12.3) находим  – прообраз функции
– прообраз функции  :
:

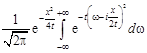 . (13.7)
. (13.7)
Последний интеграл в (13.7) равен  . Поэтому
. Поэтому
 .
.
По теореме о свертке
 ,
,
или
 . (13.8)
. (13.8)
Решение уравнения теплопроводности, записанное в виде (13.8), называется интегралом Пуассона.
Пример 3. Найти решение волнового уравнения
 , (13.9)
, (13.9)
удовлетворяющее начальным условиям
 . (13.10)
. (13.10)
Замечание. Задача Коши (13.9),(13.10) является математической моделью одномерных волновых процессов в сплошных безграничных средах. Поле возмущений в среде, выведенной из равновесного состояния, описывается функцией  , физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны
, физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны  – это отклонение струны от ее равновесного положения, функции j(х) и
– это отклонение струны от ее равновесного положения, функции j(х) и  задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа
задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа 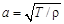 , где
, где 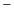 и r – натяжение и плотность струны в положении равновесия. В задачах акустики
и r – натяжение и плотность струны в положении равновесия. В задачах акустики  – скорость возмущенного движения в точке
– скорость возмущенного движения в точке  в момент времени
в момент времени  ;
;  – скорость звука в невозмущенной среде и т.д.
– скорость звука в невозмущенной среде и т.д.
Решение. Преобразуя по Фурье уравнение (13.9) и начальные условия (13.10), получим задачу Коши для обыкновенного дифференциального уравнения второго порядка:
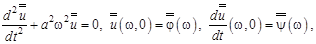
где w – параметр.
Решение задачи имеет вид

Используя (13.1) и (13.2), получим формулу Эйлера – Даламбера
 (13.11)
(13.11)
Для выяснения физического смысла полученного решения преобразуем формулу (13.11). Положим
 .
.
Тогда
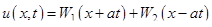 . (13.12)
. (13.12)
При 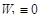 возмущение
возмущение  сохраняет постоянное значение
сохраняет постоянное значение  , если переменные
, если переменные  и
и  связаны зависимостью:
связаны зависимостью: 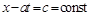 . Иными словами, возмущенное состояние
. Иными словами, возмущенное состояние  переносится в положительном направлении оси абсцисс со скоростью
переносится в положительном направлении оси абсцисс со скоростью  . Поэтому говорят, что функция
. Поэтому говорят, что функция  определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция
определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция  задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде.
задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде.
Из формулы (13.12) следует, что возмущение в точке х в момент времени  есть результат сложения волн
есть результат сложения волн  и
и  , вышедших в момент времени
, вышедших в момент времени 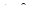 из точек с координатами
из точек с координатами  и
и  соответственно.
соответственно.
Итак, при весьма общих предположениях установлено следующее:
1. Произвольную функцию  можно представить в виде «суммы» гармоник; если
можно представить в виде «суммы» гармоник; если 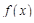 задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если
задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если 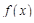 задана на всей числовой оси (но непериодическая), то эта сумма – интеграл Фурье. С точки зрения приложений, это означает, что самые разнообразные физические зависимости, скажем, давления, тока, напряжения и т.д. от времени можно представить в виде линейной суперпозиции гармонических колебаний.
задана на всей числовой оси (но непериодическая), то эта сумма – интеграл Фурье. С точки зрения приложений, это означает, что самые разнообразные физические зависимости, скажем, давления, тока, напряжения и т.д. от времени можно представить в виде линейной суперпозиции гармонических колебаний.
2. В представлении формулы 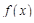 в виде ряда или интеграла Фурье естественно возникает ее спектр, который однозначно определяется по функции
в виде ряда или интеграла Фурье естественно возникает ее спектр, который однозначно определяется по функции  и который, в свою очередь, однозначно определяет саму функцию
и который, в свою очередь, однозначно определяет саму функцию 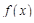 .
.
3. Результаты спектрального анализа, т.е. процесса нахождения спектра той или иной зависимости, используются при исследовании линейных систем, так как в этом случае достаточно изучить поведение системы при воздействии на нее гармонических колебаний, а затем просуммировать результаты этих воздействий с учетом спектра рассматриваемого (уже произвольного) воздействия.
Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10).
Приложения
Электрические цепи. Основными элементами электрических цепей являются сопротивления, индуктивности и емкости (конденсаторы). Каждый из этих элементов называются двухполюсником, поскольку он обладает двумя контактами (полюсами), которые соединяются с полюсами других элементов цепи. Электрическое состояние двухполюсника в каждый момент времени 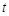 определяется двумя величинами: силой тока (током)
определяется двумя величинами: силой тока (током)  , проходящего через двухполюсник, и падением напряжения (напряжением)
, проходящего через двухполюсник, и падением напряжения (напряжением)  на его полюсах. Для каждого двухполюсника функции
на его полюсах. Для каждого двухполюсника функции 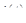 и
и  связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
Для сопротивления имеет место закон Ома
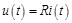 ,
,
где 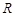 – сопротивление двухполюсника.
– сопротивление двухполюсника.
Для индуктивности справедливо соотношение
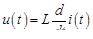 ,
,
где  – индуктивность двухполюсника.
– индуктивность двухполюсника.
Для конденсатора выполняется соотношение
 ,
,
где С – емкость конденсатора;  – начальный заряд на его обкладках.
– начальный заряд на его обкладках.
В дальнейшем будем считать, что в начальный момент времени  цепь была свободна от токов и зарядов, что соответствует задачам включения.
цепь была свободна от токов и зарядов, что соответствует задачам включения.
Если ввести операторный ток  и операторное напряжение
и операторное напряжение  как изображения функций
как изображения функций  и
и  соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
 .
.
Последние соотношения могут быть записаны в виде операторного закона Ома
 ,
,
где операторное сопротивление (импеданс)  в случае активного сопротивления, индуктивности и емкости принято в виде соответственно
в случае активного сопротивления, индуктивности и емкости принято в виде соответственно  . Величину, обратную
. Величину, обратную  ,
,  называют операторной проводимостью (адмитансом) двухполюсника.
называют операторной проводимостью (адмитансом) двухполюсника.
При последовательном соединении двух двухполюсников с операторными сопротивлениями 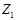 и
и  имеем
имеем  ;
; 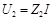 и
и  , откуда
, откуда  , и следовательно, импеданс цепи
, и следовательно, импеданс цепи  . Аналогично, при параллельном соединении двух элементов с адмитансами
. Аналогично, при параллельном соединении двух элементов с адмитансами  и
и  получим
получим 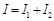 ,
,  ,
,  , откуда
, откуда  , и следовательно, адмитанс цепи
, и следовательно, адмитанс цепи  .
.
Таким образом, в задачах включения операторные сопротивления и проводимости цепей рассчитываются по обычным правилам соединения активных сопротивлений. Например, если цепь состоит из последовательно соединенных сопротивления  , индуктивности
, индуктивности  и емкости
и емкости 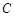 , шунтированной сопротивлением
, шунтированной сопротивлением  , то ее импеданс
, то ее импеданс  .
.
Если электрическая цепь с адмитансом  включена на эдс
включена на эдс 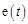 , то операторный ток в ней определяется соотношением
, то операторный ток в ней определяется соотношением  ,
,  .
.
Как правило, операторная проводимость цепи  представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости
представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости  , что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
, что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
Если эдс 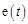 является ограниченной функцией времени, то полюсы функции
является ограниченной функцией времени, то полюсы функции  имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
имеют неотрицательные вещественные части, и следовательно (см. замечание 2 к теореме Хевисайда), по истечении достаточно длительного промежутка времени в системе устанавливается стационарный режим, при котором ток
 ,
,
где  ;
;  – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями;
с положительными мнимыми частями; 
|
|
|



 . Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье.
. Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье. ,
,  и
и 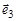 . Произвольный вектор
. Произвольный вектор  является линейной комбинацией векторов базиса:
является линейной комбинацией векторов базиса: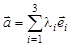 . (1.1)
. (1.1)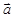 относительно базиса
относительно базиса  , могут быть определены следующим образом. Скалярное произведение вектора
, могут быть определены следующим образом. Скалярное произведение вектора 
 .
. при
при  , следовательно, в правой части последнего равенства отлично от нуля лишь одно слагаемое, соответствующее
, следовательно, в правой части последнего равенства отлично от нуля лишь одно слагаемое, соответствующее  , поэтому
, поэтому  , откуда
, откуда , (1.2)
, (1.2) .
. и
и  заданы своими координатами
заданы своими координатами  и
и  , то их скалярное произведение
, то их скалярное произведение .
.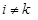 скалярное произведение
скалярное произведение  , то в двойной сумме отличны от нуля лишь слагаемые с равными индексами, поэтому
, то в двойной сумме отличны от нуля лишь слагаемые с равными индексами, поэтому . (1.3)
. (1.3) из (1.3) следует
из (1.3) следует . (1.4)
. (1.4) определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме:
определена на всей числовой оси. Считая, что на произвольном конечном промежутке [– L, L ] заданная функция удовлетворяет условиям Дирихле, представим ее тригонометрическим рядом Фурье в комплексной форме: , (11.1)
, (11.1) ; (11.2)
; (11.2) – частота k -й гармоники;
– частота k -й гармоники; 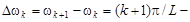
 .
.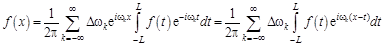 . (11.3)
. (11.3)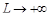 величина
величина 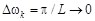 . Правая часть формулы (11.3) аналогична интегральной сумме для функции
. Правая часть формулы (11.3) аналогична интегральной сумме для функции  по переменной w в промежутке
по переменной w в промежутке  . Поэтому можно ожидать, что после перехода в (11.3) к пределу при
. Поэтому можно ожидать, что после перехода в (11.3) к пределу при  вместо ряда получим интеграл
вместо ряда получим интеграл . (11.4)
. (11.4) , во-первых, абсолютно интегрируема на промежутке
, во-первых, абсолютно интегрируема на промежутке  , т.е. интеграл
, т.е. интеграл  сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к
сходится, и, во-вторых, удовлетворяет условиям Дирихле на каждом конечном промежутке (– L, L). Тогда интеграл Фурье сходится (в смысле главного значения) всюду к  , т.е. равенство (11.4) выполняется при всех х из промежутка
, т.е. равенство (11.4) выполняется при всех х из промежутка  . Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке.
. Здесь, по-прежнему, предполагается, что в точке разрыва значение функции равно полусумме ее односторонних пределов в этой точке. . (12.1)
. (12.1) непрерывна и абсолютно интегрируема на всей оси, то функция
непрерывна и абсолютно интегрируема на всей оси, то функция  непрерывна на промежутке
непрерывна на промежутке  , то
, то , (12.2)
, (12.2)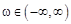 , поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция
, поэтому интеграл (12.1) сходится равномерно относительно w. Отсюда и следует, что функция  непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы).
непрерывна (точно так же, как из равномерной сходимости ряда, составленного из непрерывных функций, следует непрерывность его суммы). . (12.3)
. (12.3) , определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции
, определяемая формулой (12.1), называется преобразованием Фурье или Фурье-образом функции  . В свою очередь, формула (12.3) определяет
. В свою очередь, формула (12.3) определяет  как обратное преобразование Фурье, или прообраз функции
как обратное преобразование Фурье, или прообраз функции  . Равенство (12.3) при заданной функции
. Равенство (12.3) при заданной функции  задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке
задает, условно говоря, пакет комплексных гармоник с частотами, непрерывно распределенными на промежутке  и суммарной комплексной амплитудой
и суммарной комплексной амплитудой  . Функция
. Функция 
 называется спектральной плотностью. Формулу (12.2), записанную в виде
называется спектральной плотностью. Формулу (12.2), записанную в виде ,
, – Фурье-образы вещественных функций
– Фурье-образы вещественных функций  соответственно. Тогда
соответственно. Тогда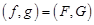 ; (12.4)
; (12.4) , (12.5)
, (12.5) . Заменив функцию
. Заменив функцию 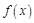 ее выражением (12.3) через Фурье-образ
ее выражением (12.3) через Фурье-образ  .
.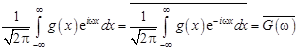 .
.  , т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при
, т.е. формула (12.4) доказана. Формула (12.5) получается из (12.4) при  .
. четна, то ее Фурье-образ, который здесь будем обозначать
четна, то ее Фурье-образ, который здесь будем обозначать  , также является вещественной четной функцией. Действительно,
, также является вещественной четной функцией. Действительно,

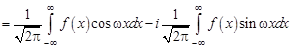 .
. . (12.6)
. (12.6)
 .
. и
и  – соответственно четная и нечетная функции переменной w, то
– соответственно четная и нечетная функции переменной w, то . (12.7)
. (12.7)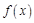 нечетна, то ее преобразование Фурье
нечетна, то ее преобразование Фурье  , где
, где  – вещественная нечетная функция от w. При этом
– вещественная нечетная функция от w. При этом ; (12.8)
; (12.8) . (12.9)
. (12.9) только для
только для  . Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке
. Поэтому косинус- и синус-преобразования Фурье можно применять и к функции, определенной на полубесконечном промежутке  . В этом случае при
. В этом случае при  интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при
интегралы в формулах (12.7) и (12.9) сходятся к заданной функции, а при  к ее четному и нечетному продолжениям соответственно.
к ее четному и нечетному продолжениям соответственно. .
. где
где  :
: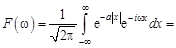


 .
.

 .
.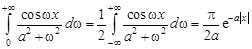 .
. , если
, если  .
.
 ;
; .
.
 .
.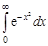 .
. , применив к функции
, применив к функции 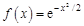 , где
, где  , преобразование Фурье и введя замену
, преобразование Фурье и введя замену 

 ;
;
 .
. , и, следовательно, с заменой
, и, следовательно, с заменой 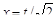 можно записать
можно записать .
. ;
;  .
. ,
, является Фурье-образом функции
является Фурье-образом функции  , будем обозначать в дальнейшем одним из следующих способов:
, будем обозначать в дальнейшем одним из следующих способов: 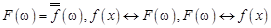 .
.
 , где
, где  . Это свойство сразу следует из определения (12.1) и линейности операции интегрирования.
. Это свойство сразу следует из определения (12.1) и линейности операции интегрирования. , где
, где  . Обозначив
. Обозначив  , получим
, получим
 , где
, где 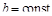 . Введя замену
. Введя замену  , получим
, получим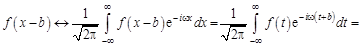
 .
. , (13.1)
, (13.1) . Действительно,
. Действительно,
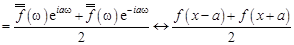 .
. и
и  называется функция
называется функция .
. :
:  .
.

 ,
, , получим
, получим
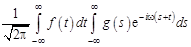 =
=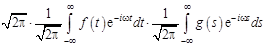 =
=  ,
, и ее производная
и ее производная  абсолютно интегрируемы на промежутке
абсолютно интегрируемы на промежутке 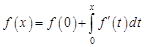 .
.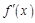 интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при
интегрируема на всей оси, интеграл в правой части последнего равенства имеет конечный предел при  . Следовательно, существует конечный предел
. Следовательно, существует конечный предел 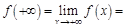
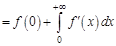 . При этом
. При этом  , ибо в противном случае функция
, ибо в противном случае функция 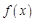 была бы неинтегрируемой на промежутке
была бы неинтегрируемой на промежутке 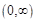 . Точно также доказывается, что
. Точно также доказывается, что  .
. .
. .
. .
. соответствует операция умножения ее Фурье-образа на множитель
соответствует операция умножения ее Фурье-образа на множитель  . Аналогично, если функция
. Аналогично, если функция  имеет абсолютно интегрируемые производные до n- го порядка включительно, то
имеет абсолютно интегрируемые производные до n- го порядка включительно, то
 ,
,  .
. , (13.2)
, (13.2) .
.
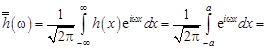

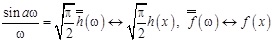 ,
,
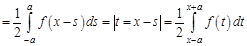 .
. (13.3)
(13.3) , удовлетворяющее начальному условию
, удовлетворяющее начальному условию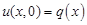 . (13.4)
. (13.4) , проинтегрируем его по х от
, проинтегрируем его по х от  до
до  . Тогда
. Тогда
 , (13.5)
, (13.5)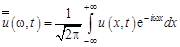 – Фурье-образ функции
– Фурье-образ функции  .
. .
. переменной t, где w – параметр.
переменной t, где w – параметр. . (13.6)
. (13.6) .
. – прообраз функции
– прообраз функции  :
:
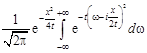 . (13.7)
. (13.7) . Поэтому
. Поэтому .
. ,
, . (13.8)
. (13.8) , (13.9)
, (13.9) . (13.10)
. (13.10) , физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны
, физический смысл которой определяется спецификой рассматриваемой задачи. В задаче о малых поперечных колебаниях струны  – это отклонение струны от ее равновесного положения, функции j(х) и
– это отклонение струны от ее равновесного положения, функции j(х) и  задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа
задают соответственно форму струны и распределение скоростей ее точек в начальный момент времени. Константа 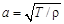 , где
, где  и r – натяжение и плотность струны в положении равновесия. В задачах акустики
и r – натяжение и плотность струны в положении равновесия. В задачах акустики  в момент времени
в момент времени  ;
;  – скорость звука в невозмущенной среде и т.д.
– скорость звука в невозмущенной среде и т.д.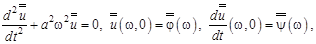

 (13.11)
(13.11) .
.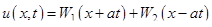 . (13.12)
. (13.12)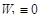 возмущение
возмущение  сохраняет постоянное значение
сохраняет постоянное значение  , если переменные
, если переменные  и
и  связаны зависимостью:
связаны зависимостью: 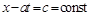 . Иными словами, возмущенное состояние
. Иными словами, возмущенное состояние  переносится в положительном направлении оси абсцисс со скоростью
переносится в положительном направлении оси абсцисс со скоростью  . Поэтому говорят, что функция
. Поэтому говорят, что функция  определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция
определяет бегущую волну, перемещающуюся вправо со скоростью а. Аналогично, функция  задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде.
задает волну, распространяющуюся влево с той же скоростью а. Таким образом, выяснен физический смысл постоянной величины а в уравнении (13.9): а – это скорость распространения возмущений в среде. есть результат сложения волн
есть результат сложения волн  и
и  , вышедших в момент времени
, вышедших в момент времени 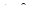 из точек с координатами
из точек с координатами  и
и  соответственно.
соответственно. можно представить в виде «суммы» гармоник; если
можно представить в виде «суммы» гармоник; если 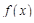 задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если
задана на конечном интервале (или периодическая), то эта сумма представляет собой ряд Фурье; если  и который, в свою очередь, однозначно определяет саму функцию
и который, в свою очередь, однозначно определяет саму функцию 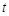 определяется двумя величинами: силой тока (током)
определяется двумя величинами: силой тока (током)  , проходящего через двухполюсник, и падением напряжения (напряжением)
, проходящего через двухполюсник, и падением напряжения (напряжением)  на его полюсах. Для каждого двухполюсника функции
на его полюсах. Для каждого двухполюсника функции 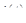 и
и  связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.
связаны некоторым соотношением, представляющим собой физический закон, управляющий работой двухполюсника.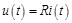 ,
,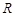 – сопротивление двухполюсника.
– сопротивление двухполюсника.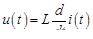 ,
, – индуктивность двухполюсника.
– индуктивность двухполюсника. ,
, – начальный заряд на его обкладках.
– начальный заряд на его обкладках. цепь была свободна от токов и зарядов, что соответствует задачам включения.
цепь была свободна от токов и зарядов, что соответствует задачам включения. и операторное напряжение
и операторное напряжение  как изображения функций
как изображения функций  и
и  соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие:
соответственно, то вышеприведенные уравнения, управляющие работой двухполюсников, перейдут в следующие: .
. ,
, . Величину, обратную
. Величину, обратную  ,
,  называют операторной проводимостью (адмитансом) двухполюсника.
называют операторной проводимостью (адмитансом) двухполюсника.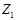 и
и  имеем
имеем  ;
; 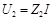 и
и  , откуда
, откуда  , и следовательно, импеданс цепи
, и следовательно, импеданс цепи  . Аналогично, при параллельном соединении двух элементов с адмитансами
. Аналогично, при параллельном соединении двух элементов с адмитансами  и
и  получим
получим 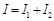 ,
,  ,
,  , откуда
, откуда  , и следовательно, адмитанс цепи
, и следовательно, адмитанс цепи  .
. , индуктивности
, индуктивности  и емкости
и емкости 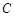 , шунтированной сопротивлением
, шунтированной сопротивлением  , то ее импеданс
, то ее импеданс  .
.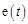 , то операторный ток в ней определяется соотношением
, то операторный ток в ней определяется соотношением  ,
,  .
. представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости
представляет собой рациональную дробь, полюсы (корни знаменателя) которой расположены в левой полуплоскости  , что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний.
, что, как следует из теоремы Хевисайда, гарантирует устойчивость системы, т.е. исключает возможность возникновения в такой системе незатухающих свободных колебаний. ,
, ;
;  – чисто мнимые полюсы функции
– чисто мнимые полюсы функции  с положительными мнимыми частями;
с положительными мнимыми частями;