Единичная функция Хевисайда. Имеем:

Так как при  , то
, то
 .
.
Для функции Хевисайда с запаздывающим аргументом  по теореме запаздывания получим
по теореме запаздывания получим

Экспонента. По теореме смещения

Гиперболические и тригонометрические функции. В силу линейности преобразования Лапласа имеем
 ;
;
 ;
;
 ;
;
 .
.
Степенная функция с натуральным показателем. Положим  , где
, где  . Тогда при
. Тогда при 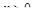
 .
.
При  , поэтому
, поэтому

Отсюда
 .
.
Так как  , то
, то

Упражнение 1. Найти, используя теорему смещения, Лаплас-образы оригиналов 
Периодические функции. Если оригинал 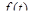 является Т-периодической функцией, то его изображение по Лапласу
является Т-периодической функцией, то его изображение по Лапласу
 (15.1)
(15.1)
Действительно, в этом случае
 .
.
Выполнив замену  , в силу периодичности
, в силу периодичности 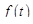 будем иметь
будем иметь

 .
.
Ряд в правой части последнего равенства представляет собой сумму бесконечной геометрической прогрессии со знаменателем  Так как при
Так как при 
 , то ряд сходится, и его сумма равна
, то ряд сходится, и его сумма равна  , откуда и следует доказываемое утверждение.
, откуда и следует доказываемое утверждение.
Пример. Найти Лаплас-образ оригинала  с периодом Т = 1).
с периодом Т = 1).
Решение. Имеем

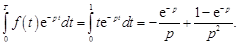
Следовательно, в силу (15.1)
 .
.
Ступенчатые (кусочно-постоянные) функции. Ступенчатая функция  , где
, где  , а числа
, а числа  образуют возрастающую последовательность, может быть представлена в виде
образуют возрастающую последовательность, может быть представлена в виде
 ,
, 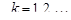 ,
,
где 
Тогда
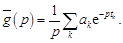
Упражнение 2. Найти изображение кусочно-постоянной функции 
Импульсные функции. Импульсной функцией будем называть функцию вида

где 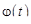 – функция, определенная для всех
– функция, определенная для всех 
Используя функцию Хевисайда с запаздывающим аргументом, можем записать
 .
.
Введем функции 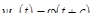 , где
, где  . Тогда
. Тогда 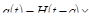
 , и по теореме запаздывания
, и по теореме запаздывания
 .
.
Пример. Найти Лаплас-образ импульсной функции
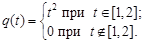
Решение. Так как
 ;
;
 ;
;
 ,
,
то
 .
.
Дельта-функция Дирака. Рассмотрим семейство ступенчатых импульсных функций
 (15.2)
(15.2)
и семейство их изображений по Лапласу
 . (15.3)
. (15.3)
При  семейство функций
семейство функций  расходится, так как
расходится, так как

Введем условную функцию  – дельта-функцию Дирака, которую будем считать пределом семейства (15.2):
– дельта-функцию Дирака, которую будем считать пределом семейства (15.2):  . Таким образом, дельта-функция равна нулю всюду, кроме точки
. Таким образом, дельта-функция равна нулю всюду, кроме точки  , где она равна
, где она равна  .
.
Изображением дельта-функции условимся считать предел семейства (15.3) при  :
:
 .
.
Далее по определению положим
 ;
;  .
.
Можно доказать (и это следует сделать самостоятельно) справедливость следующих утверждений:
 (15.4)
(15.4)
 (15.5)
(15.5)

 (15.6)
(15.6)
Выражения (15.5) и (15.6) корректны только при условии непрерывности функции f (t).
Замечание 1. Из утверждения (15.6) следует, что
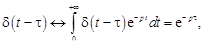
что полностью соответствует теореме запаздывания.
Замечание 2. В силу (15.4) имеем
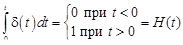 .
.
Таким образом, дельта-функцию формально можно рассматривать как производную единичной функции Хевисайда.
В прикладных дисциплинах дельта-функции широко используются для моделирования ударных сил, сосредоточенных нагрузок и тому подобных явлений.




 , то
, то .
. по теореме запаздывания получим
по теореме запаздывания получим

 ;
; ;
; ;
; .
. , где
, где  . Тогда при
. Тогда при 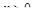
 .
. , поэтому
, поэтому
 .
. , то
, то

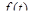 является Т-периодической функцией, то его изображение по Лапласу
является Т-периодической функцией, то его изображение по Лапласу (15.1)
(15.1) .
. , в силу периодичности
, в силу периодичности 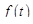 будем иметь
будем иметь
 .
. Так как при
Так как при 
 , то ряд сходится, и его сумма равна
, то ряд сходится, и его сумма равна  , откуда и следует доказываемое утверждение.
, откуда и следует доказываемое утверждение. с периодом Т = 1).
с периодом Т = 1).
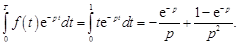
 .
. , где
, где  , а числа
, а числа  образуют возрастающую последовательность, может быть представлена в виде
образуют возрастающую последовательность, может быть представлена в виде ,
, 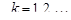 ,
,
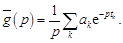


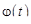 – функция, определенная для всех
– функция, определенная для всех 
 .
.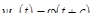 , где
, где  . Тогда
. Тогда 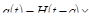
 , и по теореме запаздывания
, и по теореме запаздывания .
.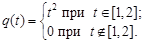
 ;
; ;
; ,
, .
. (15.2)
(15.2) . (15.3)
. (15.3) семейство функций
семейство функций  расходится, так как
расходится, так как
 – дельта-функцию Дирака, которую будем считать пределом семейства (15.2):
– дельта-функцию Дирака, которую будем считать пределом семейства (15.2):  . Таким образом, дельта-функция равна нулю всюду, кроме точки
. Таким образом, дельта-функция равна нулю всюду, кроме точки  , где она равна
, где она равна  .
. .
. ;
;  .
. (15.4)
(15.4) (15.5)
(15.5)
 (15.6)
(15.6)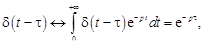
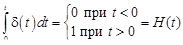 .
.


