Из формулы (3.3) с учетом того, что величина  по определению не отрицательна, следует
по определению не отрицательна, следует
 . (4.1)
. (4.1)
Левая часть неравенства (4.1) представляет собой частичную сумму положительного числового ряда
 . (4.2)
. (4.2)
Положительный ряд с ограниченными в совокупности частичными суммами сходится, следовательно, сходится и ряд (4.2). Переходя в (4.1) к пределу при  , получим неравенство Бесселя
, получим неравенство Бесселя
 . (4.3)
. (4.3)
Возвращаясь к формуле (3.3), заметим, что с увеличением п величина  уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность
уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность  сходится. из (3.3) получим ее предел
сходится. из (3.3) получим ее предел
 . (4.4)
. (4.4)
Если  , где
, где  – частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции
– частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции  . В этом случае из (4.4) следует
. В этом случае из (4.4) следует
 (4.5)
(4.5)
Соотношение (4.5) называется равенством Парсеваля. Это аналог формулы (1.4) для квадрата модуля вектора.
Замечание. Из сходимости ряда в среднем, вообще говоря, не следует его сходимость в обычном смысле слова.
Если равенство Парсеваля выполняется для всех функций из множества  , или, что то же самое, для любой функции из
, или, что то же самое, для любой функции из 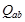 ряд Фурье сходится в среднем к этой функции, то ортогональная система
ряд Фурье сходится в среднем к этой функции, то ортогональная система  называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в §3. Доказательство этого факта выходит за рамки настоящего пособия.
называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в §3. Доказательство этого факта выходит за рамки настоящего пособия.
Свойства замкнутых систем следующие:
1. Если непрерывная функция  ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что
ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что  , и тогда (см. § 2,свойство нормы 2)
, и тогда (см. § 2,свойство нормы 2) 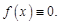
Таким образом, к замкнутой системе функций 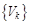 нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем
нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем  . Это свойство замкнутой системы функций называют ее полнотой.
. Это свойство замкнутой системы функций называют ее полнотой.
Следствие. Если две непрерывные функции  и
и  имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно.
имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно.
2. Пусть  и
и  – коэффициенты Фурье функций
– коэффициенты Фурье функций 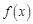 и
и  относительно замкнутой ортогональной системы
относительно замкнутой ортогональной системы  . Тогда
. Тогда
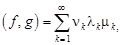 (4.6)
(4.6)
где, как и ранее, 
Соотношение (4.6) называется обобщенным равенством Парсеваля. Это аналог формулы (1.3) для скалярного произведения векторов.
Так как для функций  коэффициенты Фурье, очевидно, равны
коэффициенты Фурье, очевидно, равны  , в силу замкнутости системы из (4.5) следует
, в силу замкнутости системы из (4.5) следует

Вычитая почленно эти равенства и используя тождества

получим равенство (4.6).
3. Если  – замкнутая ортогональная система функций, то
– замкнутая ортогональная система функций, то
 , (4.7)
, (4.7)
т.е. интеграл от функции 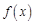 можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям
можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям  и
и

и учесть, что в этом случае  . Тогда
. Тогда

Отметим, что справедливость формулы (4.7) установлена даже без предположения о сходимости ряда Фурье.
Упражнение. Доказать, что если ряд Фурье сходится равномерно на промежутке [ а, b ] к функции  , то он сходится в среднем к этой функции.
, то он сходится в среднем к этой функции.
§ 5. Тригонометрический ряд Фурье на промежутке [– L, L ]
Система функций
 (5.1)
(5.1)
ортогональна на промежутке [– L, L ] (см. упражнение в § 3).
Показать, что  следует самостоятельно.
следует самостоятельно.
Каждой функции  , кусочно-непрерывной на промежутке [– L, L ], сопоставим ее ряд Фурье:
, кусочно-непрерывной на промежутке [– L, L ], сопоставим ее ряд Фурье:

 . (5.2)
. (5.2)
Коэффициенты Фурье  , в соответствии с (3.1), определятся формулами
, в соответствии с (3.1), определятся формулами


 (5.3)
(5.3)
Ряд (5.2) называется тригонометрическим рядом Фурье.
Как отмечалось в § 4, система функций (5.1) является замкнутой. Поэтому для любой кусочно-непрерывной функции  ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
 . (5.4)
. (5.4)
Левая часть последнего равенства, как легко видеть, представляет собой удвоенное среднее значение квадрата функции  на промежутке [– L, L ].
на промежутке [– L, L ].
Частичные суммы
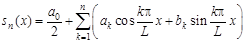
тригонометрического ряда (5.2) называются тригонометрическими полиномами Фурье. Из формулы (3.3) следует, что средняя квадратическая погрешность, возникающая при замене функции  ее тригонометрическим полиномом Фурье,
ее тригонометрическим полиномом Фурье,

 . (5.5)
. (5.5)



 по определению не отрицательна, следует
по определению не отрицательна, следует . (4.1)
. (4.1) . (4.2)
. (4.2) , получим неравенство Бесселя
, получим неравенство Бесселя . (4.3)
. (4.3) уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность
уменьшается, оставаясь неотрицательной. Следовательно, монотонно убывающая неотрицательная последовательность  сходится. из (3.3) получим ее предел
сходится. из (3.3) получим ее предел . (4.4)
. (4.4) , где
, где  – частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции
– частичная сумма ряда Фурье (3.2), то говорят, что ряд (3.2) сходится в среднем к функции  . В этом случае из (4.4) следует
. В этом случае из (4.4) следует (4.5)
(4.5) , или, что то же самое, для любой функции из
, или, что то же самое, для любой функции из 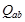 ряд Фурье сходится в среднем к этой функции, то ортогональная система
ряд Фурье сходится в среднем к этой функции, то ортогональная система  называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в §3. Доказательство этого факта выходит за рамки настоящего пособия.
называется замкнутой, а соотношение (4.5) – уравнением замкнутости. Замкнутыми системами, например, являются системы функций из упражнения в §3. Доказательство этого факта выходит за рамки настоящего пособия. ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что
ортогональна всем функциям замкнутой системы, то она тождественно равна нулю. Действительно, в этом случае все коэффициенты Фурье равны нулю. Из (4.5) следует, что  , и тогда (см. § 2,свойство нормы 2)
, и тогда (см. § 2,свойство нормы 2) 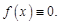
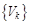 нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем
нельзя присоединить никакой новой функции, отличной от тождественного нуля, которая была бы ортогональна ко всем  . Это свойство замкнутой системы функций называют ее полнотой.
. Это свойство замкнутой системы функций называют ее полнотой. и
и  имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно.
имеют одни и те же коэффициенты Фурье, то они тождественно совпадают. Доказательство этого утверждения следует найти самостоятельно. и
и  – коэффициенты Фурье функций
– коэффициенты Фурье функций 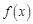 и
и  относительно замкнутой ортогональной системы
относительно замкнутой ортогональной системы  . Тогда
. Тогда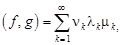 (4.6)
(4.6)
 коэффициенты Фурье, очевидно, равны
коэффициенты Фурье, очевидно, равны  , в силу замкнутости системы из (4.5) следует
, в силу замкнутости системы из (4.5) следует

 – замкнутая ортогональная система функций, то
– замкнутая ортогональная система функций, то , (4.7)
, (4.7)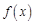 можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям
можно получить почленным интегрированием ее ряда Фурье. Для доказательства достаточно применить формулу (4.6) к функциям  и
и
 . Тогда
. Тогда
 , то он сходится в среднем к этой функции.
, то он сходится в среднем к этой функции. (5.1)
(5.1) следует самостоятельно.
следует самостоятельно.
 . (5.2)
. (5.2) , в соответствии с (3.1), определятся формулами
, в соответствии с (3.1), определятся формулами

 (5.3)
(5.3) ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид
ее ряд Фурье (5.2) сходится в среднем к этой функции. Равенство Парсеваля (4.5) в принятых теперь обозначениях примет вид . (5.4)
. (5.4)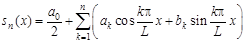

 . (5.5)
. (5.5)

