

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
По способу проведения различают
пассивные,
активные,
Активные с программным управлением,
Активные с обратной связью,
Полное уравнение физического процесса, может быть представлено зависимостью между критериями подобия, т.е. зависимостью между безразмерными величинами, определенным образом полученных из уравнения процесса.
Первая и вторая теоремы были выведены из предположения, что подобие явлений уже установленный факт.
Возникает вопрос: по каким признакам можно определить подобие явлений?
Ответ дает третья теорема подобия (теорема М.В.Кирпичева и А.А.Гухмана).
Н еобходимыми и достаточными условиями для подобия является пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия сопоставляемых явлений.
К условиям однозначности относятся следующие, не зависящие от механизма самого явления:
• геометрические свойства системы, в которой протекает процесс;
• физические параметры среды и тел, образующих систему;
• начальное состояние системы (начальные условия);
• условия на границах системы (граничные или краевые условия);
• взаимодействие объекта и внешней среды.
Необходимым условием подобия двух объектов является одинаковый вид системы уравнений.
Критерии подобия – безразмерные комбинации, которые составлены из физических величин, описывающих процессы в исследуемых объектах.
Принято обозначать критерии подобия буквой π. При экспериментах необходимо измерять все величины, входящие в критерий. Обрабатывать результаты следует в виде зависимостей между критериями подобия.
Если процесс в объекте характеризуется m фундаментальными физическими величинами, для выражения размерностей которых используется k основных единиц, то этот процесс можно описать m-k безразмерными комбинациями, составленными из этих величин.
|
|
Из теоремы следуют два важных практических вывода:
Первый – уравнения, описывающие физические процессы, могут быть выражены уравнениями связи между безразмерными комбинациями – критериями подобия. Эти уравнения будут справедливы для всех подобных объектов.
второй - число независимых критериев равно m-k.
Типовые законы распределения
Для изучения основных законов распределения вероятностей введем понятие индикатора случайного события А – это дискретная случайная величина X, которая равна 1 при осуществлении события А и 0 при осуществлении 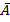 :
:
Ряд распределения вероятностей индикатора случайного события:
| xi | 0 | 1 |
| pi | q | p |
где p – вероятность осуществления А;
q = 1 – p – вероятность осуществления 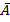 :.
:.
Числовые характеристики индикатора случайного события: mx = p, Dx = qp.
Геометрическое распределение
имеет дискретная случайная величина Х, если она принимает значения 0, 1, …, ¥ с вероятностями: p(X =_ i) =_ pi = q p,
где p – параметр распределения (0 ≤ p ≤1), q= 1 – p.
Числовые характеристики геометрического распределения: mx = q p; Dx =q/ p2.
Условия возникновения. Проводится ряд одинаковых независимых опытов до первого появления некоторого события А. Случайная величина Х – число проведенных безуспешных опытов до первого появления события А.
Биномиальное распределение
имеет дискретная случайная величина X, если она принимает значения 0, 1, …, n со следующими вероятностями p(X =_ i) =_ pi = 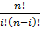 pi q n - I,
pi q n - I,
где n, p – параметры распределения (0 ≤ p ≤ 1), q = 1 – p.
Числовые характеристики биномиального распределения: mx = np; Dx = nqp.
Условия возникновения. Проводится n одинаковых независимых испытаний, в каждом из которых событие А появляется с вероятностью р. Случайная величина Х – число опытов, в которых произошло событие А.
|
|
Распределение Пуассона
имеет дискретная случайная величина Х, если она принимает значения 0, 1, …, ¥ со следующими вероятностями: p(X =_ i) =_ pi = 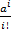 e– a,
e– a,
где a – параметр распределения (a > 0).
Числовые характеристики пуассоновской случайной величины: mx = a, Dx=a.
Условия возникновения:
1. Распределение Пуассона является предельным случаем биномиального, когда число опытов n неограниченно увеличивается, а вероятность p события A в одном опыте стремится к 0, так что существует предел  = a.
= a.
2. Случайная величина Х – число событий пуассоновского
потока, поступивших в течение интервала t, причем параметр а = τλ,
где λ – интенсивность потока.
Последовательность (во времени) моментов возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание и т.п.) называется потоком случайныхсобытий.
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал t, в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени λ(интенсивность потока) постоянно.
Поток случайных событий называется ординарным, если вероятность попадания в некоторый участокD t двух и более случайных событий значительно меньше, чем вероятность попадания 1-го события.
В потоке отсутствует последействие, если вероятность попадания событий на участок t не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Поток случайных событий называется пуассоновским или простейшим, если он является стационарным, ординарным и без последействия.
Равномерное распределение
|

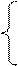 0, x < a
0, x < a
f(x) = 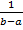 , a £ x £ b
, a £ x £ b
0, x > b
Числовые характеристики равномерно распределенной случайной величины:
mx = (a + b)/2; Dx= (b – a)2/12
При необходимости определения параметров a и b по известным mx, Dx используют следующие формулы: a = mx – s x 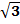 , b = mx + s x
, b = mx + s x 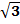 .
.
Условия возникновения:
1. Случайная величина Х – ошибки округления при ограниченной разрядной сетке:
|
|
– округление до меньшего целого, X [–1; 0], mx = – 0,5;
– округление до большего целого, X [–0; 1], mx = 0,5;
– округление до ближайшего целого, X [– 0,5; 0,5], mx = 0, где 1 – вес младшего разряда.
2. Случайная величина Х – погрешность считывания значений с аналоговой шкалы измерительного прибора, X [– 0,5; 0,5], mx = 0, где 1– цена деления шкалы.
3. Генераторы псевдослучайных величин, например RANDOM, встроенные в языки программирования высокого уровня.
Распределение Стьюдента
Распределение Стьюдента (t –распределение) имеет важное значение при статистических вычислениях, связанных с нормальным законом, а именно тогда, когда среднее квадратичное отклонение σ неизвестно и подлежит определению по опытным данным.
Пусть Y: Y1, Y2,..., Yn – независимые случайные величины, имеющие нормальное распределение с параметрами M (Y)=M (Yi)=0 и σ Y = σ Yi =1, i =1,… n.
Закон сложения ошибок
Для независимых случайных величин свойством аддитивности обладают дисперсии.
Для Z 1 = a 1 X 1 + a 2 X 2 + … + a n Xn
выборочная дисперсия 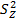 =
= 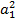
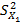 + … +
+ … + 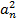
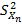 .
.
При a 1= a 2= … = a n имеем Z =  (X 1 + X 2 + … + Xn) =
(X 1 + X 2 + … + Xn) = 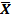 и
и 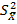 =
= 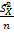 , где
, где
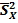 =
= 
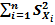 . Если X 1, X, … Xn – независимые n наблюдений Х, то
. Если X 1, X, … Xn – независимые n наблюдений Х, то 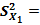
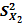 =
= 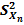 =
= 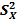 , то
, то 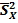 =
= 
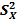
Ошибки косвенных измерений
Измерения делятся на прямые и косвенные. При косвенных измерениях определяемую величину определяется как функцию от непосредственно измеряемых величин.
Пусть между случайными величинами z и x 1 , x 2 … x n есть известная функциональная зависимость: z = f (x 1 , x 2 … x n)
Истинное значение величины z может не совпадать с математическим ожиданием Mz, а определяется тем же законом: aZ = f ( 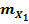 , …
, … 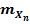 ).
).
Величина aZ – среднее косвенного измерения.
На практике определяют выборочные дисперсии 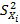 и по ним выборочную дисперсию косвенного измерения
и по ним выборочную дисперсию косвенного измерения 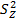 , которая служит оценкой генеральной дисперсии
, которая служит оценкой генеральной дисперсии 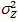 .
.
По закону сложения дисперсий: 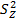 =
= 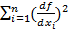
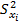 – закон накопления ошибок.
– закон накопления ошибок.
Критерий Н.В.Смирнова
Если известно, что есть только одно аномальное значение, то оно будет крайним членом вариационного ряда (т.е. ряда наблюдений, расположенных в возрастающей последовательности: x 1 £ x 2 £ …£ xn). Поэтому проверять выборку на наличие одной грубой ошибки естественно при помощи статистики
|
|
u 1 =  или un =
или un = 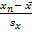
При выбранном уровне значимости α (α=0,1; 0,05; 0,01 при объеме выборки от 3 до 20 опытов) критическая область для критерия Н.В.Смирнова строится следующим образом: u 1 > u a, n или un > u a, n. В этом случае значения х 1 или х n исключают из рассмотрения,
Критерий Пирсона
Для проверки согласованности распределений, полученных по выборке с некоторой теоретической плотностью распределения.
Отличие оценки закона распределения P от теоретического закона распределения Р* можно охарактеризовать величиной
c 2 = 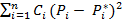 , где
, где
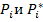 – оценка и теоретическая вероятность случайной величины для i-ого интервала;
– оценка и теоретическая вероятность случайной величины для i-ого интервала; 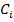 – весовые коэффициенты, которые с большим весом учитывают отклонения для меньших
– весовые коэффициенты, которые с большим весом учитывают отклонения для меньших 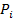 .
.
Пирсон выбрал весовые коэффициенты следующим образом: 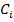 =
= 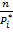 При таком выборе
При таком выборе 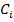 закон распределения c 2 слабо зависит от n и P(x), а определяется в основном числом разрядов k ( количеством интервалов ):
закон распределения c 2 слабо зависит от n и P(x), а определяется в основном числом разрядов k ( количеством интервалов ):
c 2 = n 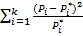 =
= 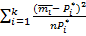 . Здесь
. Здесь 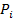 =
= 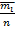
При идеальном соответствии экспериментальных данных нормальному закону, экспериментальное значение критерия Пирсона будет равно нулю.
По результатам экспериментальных измерений и предположению нормального закона их распределения определяется расчетное значение критерия Пирсона. Определяют число степеней свободы m, задаются уровнем значимости α и определяют теоретическое значение критерия Пирсона 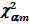 .
.
4. Если c 2 < 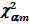 , то нуль-гипотеза о нормальном законе распределения экспериментальных данных принимается с доверительной вероятностью p = 1 – a.
, то нуль-гипотеза о нормальном законе распределения экспериментальных данных принимается с доверительной вероятностью p = 1 – a.
Критерий Колмогорова
Независимо от функции распределения вероятностей при неограниченном возрастании числа независимых наблюдений вероятность неравенства
D 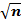 ³ l стремится к пределу P (l).
³ l стремится к пределу P (l).
Устанавливается максимальная величина модуля разности между статистической и теоретической функциями распределения вероятностей
D = | F o (x) – F (x)| max и определяется величина l = D 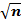 , где n – число независимых наблюдений, и по таблице находитсявероятности P (l).
, где n – число независимых наблюдений, и по таблице находитсявероятности P (l).
Величина этой вероятности P (l) свидетельствует о том, что за счет случайных причин вероятность максимального расхождения между функциями распределения будет не меньше P (l).
Если вероятность мала, гипотезу следует отвергнуть, при больших значениях вероятности эту гипотезу следует считать, как не противоречащую опытным данным.
Метод наименьших квадратов
Данный метод определения неизвестных коэффициентов уравнения регрессии был разработан Лежандром и Гауссом почти 200 лет назад.
Определение коэффициентов bj методом наименьших квадратов основано на выполнении требования, чтобы сумма квадратов отклонений экспериментальных точек от соответствующих значений уравнения регрессии была минимальна.
|
|
После дифференцирования полученная система содержит столько же уравнений, сколько неизвестных коэффициентов b 0 ,… 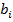 … bk входит в уравнение
… bk входит в уравнение
регрессии, и называется в математической статистике системой нормальных уравнений.
Регрессионный анализ
Как и корреляционный анализ, регрессионный включает в себя
построение уравнения регрессии (например, методом наименьших квадратов) и статистическую оценку результатов. При проведении регрессионного анализа принимаются следующие допущения:
1. Входной параметр х изменяется с весьма малой ошибкой. Появление ошибки в определении у объясняется наличием в процессе не выявленных переменных и случайных воздействий, не вошедших в уравнение регрессии.
2. Результаты наблюдений выходной величины – независимые нормально распределенные случайные величины.
3. При проведении параллельных опытов выборочные дисперсии должны быть однородны. При выполнении измерений в различных условиях возникает задача сравнения точности измерений, а это возможно осуществлять при наличии однородных дисперсий (т.е. принадлежности экспериментальных данных к одной генеральной совокупности).
После того, как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ состоит в установлении адекватности уравнения и проверке значимости коэффициентов уравнения.
Планирование экспериментов при построении квадратичной модели
В некоторых случаях существенными могут оказаться коэффициенты при квадратных переменных, их кубов и т.д.
Для двухфакторного эксперимента модель может быть представлена выражением
y = b 0 x 0+ b 1 x 1 + b 2 x 2+ b 12 x 1 x 2+ b 11 x 12 + b22 x22
Полученные вектор - столбцы 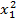 и
и 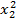 являются единичными столбцами, совпадающие друг с другом и с фиктивным столбцом x 0. Очевидно, она включает в себя значения свободного члена β0 и вклады квадратичных членов. Символически это можно записать: b 0 ® β0 +
являются единичными столбцами, совпадающие друг с другом и с фиктивным столбцом x 0. Очевидно, она включает в себя значения свободного члена β0 и вклады квадратичных членов. Символически это можно записать: b 0 ® β0 + 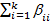
Для квадратичной модели получается следующая система смешивания:
b 0 →β0 + β11+ β22, b 1 →β1, b 2 →β2, b 12→β12.
Следовательно, планирование эксперимента на двух уровнях не дает возможности получить раздельные оценки коэффициентов при квадратичных членах и фиктивной переменной x 0.
Число уровней каждой из независимых переменных должно быть на единицу больше степени интерполяционного полинома. Для полинома второй степени число уровней должно быть равно трем.
Однако применение методов ПФЭ плана 3 n не является рациональным из-за резкого увеличения опытов эксперимента. Поэтому разработаны специальные методы построения планов второго порядка.
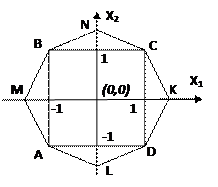 Например, в качестве двухфакторных планов второго порядка могут служить планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого (n-1) мерного правильного многоугольника (который можно вписать в круг).
Например, в качестве двухфакторных планов второго порядка могут служить планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого (n-1) мерного правильного многоугольника (который можно вписать в круг).
Пример. Имеем восьмиугольный план (рис.4.5, табл.4.6).
Получение планов второго порядка.
Для этого к ПФЭ типа 2 n добавляется центральная
точка с координатами (0,0,...0) и, так называемые,
звёздные точки с координатами (0,0,..., ±α,...,0),
лежащие на сфере диаметра 2α. Т.е. план ПФЭ
достраивается до плана второго порядка. Такой план
|
Таблица 4.6.
| Опыт | x1 | x2 | Описание |
| 1 | – 1 | – 1 | План 22 представлен квадратом ABCD |
| 2 | +1 | – 1 | |
| 3 | – 1 | +1 | |
| 4 | +1 | +1 | |
| 5 | 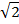
| 0 | План представлен звёздными точками KLMN
|
| 6 | – 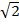
| 0 | |
| 7 | 0 | 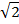
| |
| 8 | 0 | – 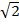
| |
| 9 | 0 | 0 | Центральная точка |
Добавление двух сфер, образованных звездными точками и центральной точкой, к ПФЭ позволяет получить раздельные оценки b 0 и b ii . Все три сферы разуют композиционный план второго порядка.
В зависимости от критерия оптимальности плана, различают ортогональное, композиционное планирование и рототабельное композиционное планирование. План, приведенный в табл. 4.6, является рототабельным и обеспечивает получение раздельных оценок b 0 и b ii.
4.11. Ортогональное центральное композиционное планирование
Критерием оптимальности является ортогональность столбцов матрицы планирования. В силу этого свойства все коэффициенты модели определяются независимо друг от друга. Оценки коэффициентов уравнения регрессии находятся с неодинаковой дисперсией. Поэтому точность предсказания выходной величины в различных направлениях факторного пространства неодинакова.
4.12. Рототабельное композиционное планирование
Обеспечивает одинаковую точность во всех направлениях на одинаковом расстоянии от центра. Критерием оптимальности в рототабельном планировании
является условие 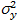 = const при одинаковом удалении точек эксперимента от центра, т.е. R = const.
= const при одинаковом удалении точек эксперимента от центра, т.е. R = const.
Примерами рототабельных планов являются планы, представляемые вершинами и, по крайней мере, одной центральной точкой любого (n-1) - мерного правильного многоугольника, который можно вписать в круг.
Композиционные центральные рототабельные планы также как и ортогональные состоят из трех сфер: сфера нулевого радиуса - центральные точки; сфера точек куба или гиперкуба и сфера звездных точек.
Равномерность расположения точек на сфере приводит к вырожденным матрицам. Для устранения вырожденности используют сферу нулевого радиуса с несколькими центральными точками.
Табл.4.7
| n | a | Na | N0 | Nc | N |
| 2 | 1,414 | 4 | 5 | 4 | 13 |
| 3 | 1,682 | 6 | 6 | 8 | 20 |
| 4 | 2 | 8 | 7 | 16 | 31 |
где Na – число звёздных точек; N0 – число точек в центре эксперимента; Nc – кол-во точек куба (гиперкуба); N – общее число точек факторного пространства.
Матрица планирования рототабельного плана второго порядка для трехфакторного эксперимента будет представлена в таблице 4.8.
Таблица 4.8.
| № опыта | x0 | x1 | x2 | x3 | x12 | x22 | x32 | x1x 2 | x1x3 | x2x3 |
| z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | |
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 2 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | -1 | -1 | +1 |
| 3 | +1 | -1 | +1 | -1 | +1 | +1 | +1 | -1 | +1 | -1 |
| 4 | +1 | +1 | +1 | -1 | +1 | +1 | +1 | +1 | -1 | -1 |
| 5 | +1 | -1 | -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 |
  6 6
| +1 | +1 | -1 | +1 | +1 | +1 | +1 | -1 | +1 | -1 |
| 7 | +1 | -1 | +1 | +1 | +1 | +1 | +1 | -1 | -1 | +1 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
| 9 | +1 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 | 0 |
| 10 | +1 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 | 0 |
| 11 | +1 | 0 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 |
| 12 | +1 | 0 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 | 0 |
| 13 | +1 | 0 | 0 | -1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 |
| 14 | +1 | 0 | 0 | +1,682 | 0 | 0 | 2,828 | 0 | 0 | 0 |
| 15 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 16 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | +1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Коэффициенты b 0 , bi, bii и bij рассчитывают по сложным формулам.
Так же рассчитывают дисперсии для T и F - критериев.
Планирование эксперимента при поиске оптимальных условий
Эксперимент, решающий эту задачу, называется экстремальным.
…требуется определить такие координаты экстремальной точки (x 1*, x 2*… xk *)
поверхности отклика y = f (x 1, x 2… xk), в которой она максимальна (минимальна).
Метод крутого восхождения
Известно, что кратчайший путь – это движение по градиенту, т.е. перпендикулярно касательным к линиям, на которых функция отклика принимает постоянные значения y = f (x 1, x 2… xk) = В.
В связи с этим при оптимизации рабочее движение целесообразно совмещать в направлении наиболее быстрого возрастания функции отклика,
Существует несколько модификаций градиентного метода, одним из них является метод крутого восхождения на рис.4.7.
В этом случае шаговое движение осуществляется в направлении наискорейшего возрастания функции отклика, т.е. grad y = f (x 1, x 2).
Однако направление корректируется не после следующего шага, а при достижении в некоторой точке на данном направлении частного экстремума функции отклика.
Рис. 4.7. Процедура оптимизации методом крутого восхождения.
Пусть в окрестности точки М0, как центра плана, поставлен ПФЭ 22
Координаты отдельных опытов соответствуют точкам 1, 2, 3, 4.
По результатам ПФЭ можно рассчитать коэффициенты линейного уравнения регрессии: 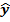 = b 0 + b 1 x 1 + b 2 x 2.
= b 0 + b 1 x 1 + b 2 x 2.
После чего можно найти градиент grad y = 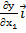 +
+ 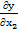
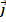 =
= 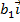 +
+ 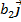
Для движения по градиенту необходимо изменять факторы пропорционально их коэффициентам регрессии в сторону, соответствующую знакам коэффициентов. В процессе поиска двигаются в этом направлении, пока не будет найден локальный максимум (т.М1). После чего находят направление градиента,
осуществляя ПФЭ. И далее процедура повторяется.
Практически алгоритм сводится к следующей последовательности операций:
1. Планирование и постановка ПФЭ (или ДФЭ) в окрестности точки начального состояния (М0). Расчет коэффициентов линейной регрессии; определение направления градиента.
2. Расчет произведений 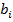 D
D 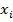 , где D
, где D 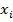 - интервал варьирования факторов при ПФЭ (ДФЭ).
- интервал варьирования факторов при ПФЭ (ДФЭ).
3. Выбор базового фактора 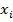 =
= 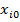 , у которого
, у которого 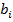 D
D 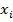 = a = max.
= a = max.
4. Выбор шага крутого восхождения для базового фактора ha производится на базе априорной информации и опыта исследователя.
Слишком большой шаг создает опасность проскакивания области оптимума.
5. Расчет шагов изменения других факторов по формуле: hi = (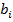 D
D 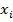 ) ha / а. Это соотношение между величинами шагов изменения отдельных факторов обеспечивает движение по градиенту в факторном пространстве.
) ha / а. Это соотношение между величинами шагов изменения отдельных факторов обеспечивает движение по градиенту в факторном пространстве.
6. Составление плана движения по градиенту: в соответствии с определенными значениями шагов изменения факторов 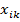 =
= 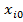 + khi, k = 1, 2..
+ khi, k = 1, 2..
Находят координаты опытов 5,6,7 по направлению градиента. Часть этих
опытов проводят «мысленно». «Мысленный» опыт заключается в получении предсказанных (расчетных) значений функции отклика по линейному уравнению регрессии, что позволяет сократить объем реальных опытов. Обычно реальные опыты ставят через 3-4 «мысленных» для того, чтобы подтвердить действительное возрастание отклика. Из опытных данных находят положение локального экстремума.
7. В окрестности локального экстремума ставят новую серию опытов (ПФЭ или ДФЭ) для определения новых значений коэффициентов уравнения регрессии и нового направления градиента. В дальнейшем процедура повторяется до достижения нового локального экстремума и т.д., вплоть до определения окрестности координат максимума функции отклика, которая носит название почти стационарной области.
Признаком достижения этой области является статистическая незначимость коэффициентов 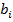 . В этой области становятся значимыми эффекты взаимодействия и квадратичные эффекты. Здесь требуется переходить от ДФЭ к ПФЭ и к планам второго порядка.
. В этой области становятся значимыми эффекты взаимодействия и квадратичные эффекты. Здесь требуется переходить от ДФЭ к ПФЭ и к планам второго порядка.
4.13.3. Симплекс-планирование
Позволяет без предварительного изучения влияния факторов найти область оптимума. Этот метод относится к безградиентным метода поиска оптимума.
Для этого используется специальный план эксперимента в виде симплекса.
Симплекс – простейший выпуклый многогранник, образованный к+1 вершинами в к -мерном пространстве, которые соединены между собой прямыми линиями: симплекс к=2 – треугольник, к=3 – тетраэдр и т.д. Симплекс называется правильным, если все расстояния между его вершинами (ребра) равны.
Координаты вершин симплекса являются значениями факторов в отдельных опытах.
Строится исходный симплекс, проводятся опыты в его вершинах и анализируются результаты.
1. Выбирается вершина, в которой получено наименьшее значение функции отклика. Для движения к оптимуму ставится опыт в новой точке, являющейся зеркальным отображением точки с наихудшим (минимальным) результатом. Процесс повторяется до тех пор, пока не будет найдена почти стационарная область.
2. Не смотря на то, что путь может быть и не прямолинеен, общее число опытов может быть небольшим.
При симплекс-планировании выбор размеров симплекса и его начальное положение произволен.
Для окончания процесса используются следующие критерии:
1 – разность значений функции отклика в вершинах симплекса становится меньше ранее заданной. Это означает вход в почти стационарную область вблизи оптимума, либо достижения области оптимума в виде «плато»;
2 - отражение любой из вершин симплекса после однократного «качания» приводит к возврату в исходное положение. При этом есть основания считать, что симплекс накрыл область оптимума.
3 – циклическое движение симплекса вокруг одной из его вершин на протяжении более, чем нескольких шагов, т.е. циркулирует вокруг области оптимума.
В случаях 2 и 3 рекомендуется уменьшать размеры симплекса, т.е. расстояние между вершинами, для уточнения координаты оптимума.
Данный метод прост, но работает не достаточно быстро. Наиболее быстрым является метод, основанный на его модификации - метод деформируемого многогранника. Ускорение достигается за счет того, что отражение осуществляется не на постоянную величину.
|
|
|
|
|
|
|





|
|
|
По способу проведения различают
пассивные,
активные,
|
|
|

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!