Магазинные автоматы.
Подобно тому, как праволинейным грамматикам соответствуют конечные автоматы, контекстно-свободным грамматикам соответствуют автоматы с магазинной памятью (МП-автоматы). В таком автомате, помимо ограниченной памяти, хранящей текущее состояние, имеется потенциально бесконечная память, используемая как стек (магазин).
При формальном определении конфигурации (мгновенного состояния) МП-автомата удобно считать все содержимое стека словом (в алфавите, в котором перечислены все возможные данные, "умещающиеся" в одной ячейке стека). Прежде чем определить конфигурацию, придется принять произвольное соглашение о том, в каком порядке записывать содержимое стека в этом слове. Например, при LL-разборе верхушка стека находится в начале слова, а при LR — в конце.
Недетерминированный конечный автомат (НКА) — по опр-ю есть пятерка
K = (Q, 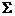 ,
, 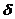 , S, F), где
, S, F), где
Q — конечное мн-во сост-й,
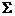 — конечное мн-во допустимых входных символов (входной алфавит),
— конечное мн-во допустимых входных символов (входной алфавит),
 r(Q) — функция переходов (отображающая множество
r(Q) — функция переходов (отображающая множество 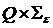 во множество подмножеств множества Q), определяющая поведение управляющего устройства,
во множество подмножеств множества Q), определяющая поведение управляющего устройства,
S — мн-во начальных состояний,
F — мн-во конечных состояний.
Автомат с магазинной памятью (МП-автомат) — это семерка
M = (Q, 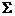 , Г,
, Г, 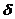 , Z 0, q 0, F), где
, Z 0, q 0, F), где
Q — -/-/-;
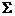 — -/-/-;
— -/-/-;
Γ — конечный алфавит магазинных символов;
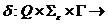 r (Q´Г*) — ф-я переходов ( r (Q´Г*) — мн-во конечных подмн-в
r (Q´Г*) — ф-я переходов ( r (Q´Г*) — мн-во конечных подмн-в 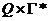 );
);
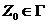 — маркер дна, символ, находящийся в магазине в начальный момент (начальный символ магазина);
— маркер дна, символ, находящийся в магазине в начальный момент (начальный символ магазина);
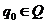 — начальное сост-е (напишем q0 или S — разницы нет, общность не нарушается);
— начальное сост-е (напишем q0 или S — разницы нет, общность не нарушается);
 — -/-/-.
— -/-/-.
Конфигурация МП-автомата — это тройка (q, w, u), где
 — текущее состояние управляющего устройства;
— текущее состояние управляющего устройства;
 — непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой (если w =
— непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой (если w = 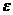 , то считается, что вся входная лента прочитана);
, то считается, что вся входная лента прочитана);
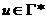 — содержимое магазина (если u =
— содержимое магазина (если u = 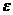 , то магазин считается пустым).
, то магазин считается пустым).
Начальной конфигурацией МП-автомата M называется конфигурация вида (q 0, w, Z 0), где  (т.е. управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0).
(т.е. управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно проанализировать, а в магазине имеется только начальный символ Z0).
Заключительной конфигурацией называется конфигурация вида (q, 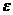 , "), где
, "), где 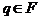 (т.е. управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана).
(т.е. управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана).
Такт работы МП-автомата M представим в виде бинарного отношения 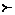 , определенного на конфигурациях:
, определенного на конфигурациях:
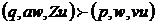 , если множество d(q, a, Z) содержит (p, v), где
, если множество d(q, a, Z) содержит (p, v), где 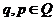 ,
, 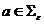 ,
,  ,
, 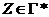 и
и 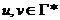 (если верхушка магазина слева).
(если верхушка магазина слева).
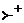 ,
, 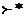 и
и 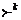 — транзитивное и рефлексивно-транзитивное замыкание отношения
— транзитивное и рефлексивно-транзитивное замыкание отношения 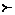 , а также его степень k > 0 соответственно.
, а также его степень k > 0 соответственно.
Говорят, что цепочка w допускается МП-автоматом M, если (q 0, w, Z 0) 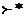 (q,
(q, 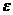 , u) для некоторых
, u) для некоторых 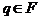 и
и 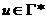 .
.
Множество всех цепочек, допускаемых автоматом M, называется языком, допускаемым (распознаваемым, определяемым) автоматом M (обозначается L (M)).
Теорема: Язык допускается МП-автоматом тогда и только тогда, когда он допускается опустошением магазина.
Теорема: Язык является контекстно-свободным тогда и только тогда, когда он допускается МП-автоматом.
Пример (скобочный автомат):
S ® aSb | e | SS — грамматика.
МПА (детерминированный), основанный на самом простом алгоритме проверки — счётчике открывающих скобок:
(® — направление стека)
| ®
| a
| b
| e
|
| q 0 Z 0
| q 0 Z 0 a
| — (отвергаем
входное слово)
| qf "
|
| q 0 a
| q 0 aa
| q 0 e
| —
|
Пример (полиндромы):
(Полиндромы — слова, кот. читаются одинаково слева направо и справа налево. Применяются в ДНК-анализе.)
Рассмотрим грамматику для полиндрома с чётным кол-вом букв:
S ® aSa | bSb | e.
Решение:
Прочитали до середины, накапливая a и b в стеке, после — начинаем стирать. Проблема: не знаем, где середина. Спасает то, что можем работать недетерминированно, предполагая середину всегда, когда это возможно.
МПА (недетерм.; Соответствующий язык — тоже недетерм.):
| ®
| a
| b
| e
|
| q 0 Z 0
| q 0 Z 0 a
| q 0 Z 0 b
| qf "
|
| q 0 a
| q 0 aa
| q 0 ab
| —
|
| q 1 e
|
| q 0 b
| q 0 ba
| q 0 bb
| —
|
| q 1 e
|
| q 1 a
| q 1 e
| —
| —
|
| q 1 b
| —
| q 1 e
| —
|
| q 1 Z 0
| —
| —
| qf "
|
Признаки недетерминированности МПА:
1) Наличие в какой-либо клетке таблицы более 1 варианта поведения;
2) Наличие в как-либо строке таблицы (q Г) как переходов, так и e-переходов.
Разбор.
Задача разбора состоит в
1) ответе на вопрос, принадлежит ли заданная цепочка языку,
2) (если да) в восстановлении дерева вывода(дерева разбора) для этой цепочки.
Методы построения дерева вывода разбиваются на два больших класса восходящие и нисходящие — в соответствии с порядком построения дерева разбора. В современных компиляторах применяются как нисходящие, так и восходящие методы.
2.1. Разбор сверху-вниз (предсказывающий, нисходящий):
Нисходящие методы начинаются с корня дерева и пытаются так его наращивать, чтобы последующие узлы дерева соответствовали синтаксису анализируемого выражения. (Появились сразу после изобретения грамматик.)
Главная задача предсказывающего разбора — определение правила вывода, которое нужно применить к нетерминалу.
LL-разбор:
(1-я L значит, что входную цепочку читаем слева направо, 2-я L — дерево разбора строим слева.)
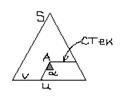
Шаблоны правил LL-разбора:
1) d(q, e, A) ' (q, a);
2) d(q, a, a) = {(q, e)}.
LL-анализатор называется LL(k)-анализатором, если данный анализатор использует предпросмотр на k символов при разборе входного потока. Грамматика, которая может быть распознана LL(k)-анализатором без возвратов к предыдущим символам, называется LL(k)-грамматикой.
2.2. Разбор снизу-вверх типа сдвиг-свертка (восходящий):
В процессе разбора снизу-вверх типа свертка-перенос строится дерево разбора входной цепочки, начиная с листьев к корню. Этот процесс можно рассматривать как «свертку» цепочки w к начальному символу грамматики. На каждом шаге свертки подцепочка, которую можно сопоставить правой части некоторого правила вывода, заменяется символом левой части этого правила вывода, и если на каждом шаге выбирается правильная подцепочка, то в обратном порядке прослеживается правосторонний вывод.
Для удобства свёртки (см. дальшв 1-м шаблоне: a) в LR-разборе используется понятие расширенного МПА:
M = (Q, 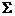 , Г,
, Г, 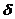 , Z 0, q 0, F),
, Z 0, q 0, F),
где смысл всех символов тот же, что и для обычного МП-автомата, кроме d, представляющего собой отображение конечного подмножества множества  (разница в *) во множество конечных подмножеств множества
(разница в *) во множество конечных подмножеств множества 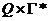 .
.
Теорема: Пусть M = (Q, 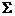 , Г,
, Г, 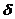 , Z 0, q 0, F) — расширенный МП-автомат. Тогда существует МП-автомат M', такой, что L (M') = L (M).
, Z 0, q 0, F) — расширенный МП-автомат. Тогда существует МП-автомат M', такой, что L (M') = L (M).
(Т.е. понятия приводятся друг к другу.)
LR-разбор:
(L — входная цепочка читается слева направо, R — дерево разбора строится справа.)

Шаблоны правил LR-разбора:
1) d(q, e, a) ' (q, A) — свёртка;
2) d(q, a, e) ' (q, a) — перенос.
Не пишем «=», п.ч. заранее не знаем, будем делать перенос или свёртку.
Грамматика называется LR(0)-грамматикой, если в ней нет конфликтов типа сдвиг/свертка и свертка/свертка ни для одного слова S.
Для выбора между сдвигом или сверткой в LR(0)-разборе используется только состояние стека. В LR(k)-разборе учитывается также k первых символов непросмотренной части входной цепочки (т.наз. аванцепочка).
Грамматика, которая может быть проанализирована LR-анализатором, заглядывая на k входных символов на каждом шаге, называется LR(k)-грамматикой.
13) Синтаксически управляемые схемы.
СУ-схемы.
Автоматы с магазинной памятью были нужны для того, чтобы ответить на вопрос, принадлежит ли слово языку + выдать дерево разбора, если да.
СУ-схемы (синтаксически управляемые) имеют на выходе новую цепочку (итоговую программу (например, на Assembler’е)). Фактически, такая схема представляет собой КС-грамматику, в которой к каждому правилу добавлен элемент перевода. Всякий раз, когда правило участвует в выводе входной цепочки, с помощью элемента перевода вычисляется часть выходной цепочки, соответствующая части входной цепочки, порожденной этим правилом.
Грамматика — это четверка
G = (N, S, P, S), где
N — алфавит нетерминальных символов;
S — алфавит терминальных символов,
P — конечное множество правил вида a®b, где aÎ(NÈS)*N(NÈS)*, bÎ(NÈS)*,
S — начальный знак (или аксиома) грамматики.
Cхемой синтаксически управляемого перевода (или трансляции, сокращенно: СУ-схемой) называется пятерка
Tr = (N, S, D, R, S), где
N — конечное мн-во нетерминальных символов (алфавит);
S — конечный входной алфавит;
D — конечный выходной алфавит;
R — конечное мн-во правил перевода вида A ® a, b, где a Î(N ÈS)*, b Î(N ÈD)* и вхождения нетерминалов в цепочку a образуют перестановку вхождений нетерминалов в цепочку b, так что каждому вхождению нетерминала B в цепочку a соответствует некоторое вхождение этого же нетерминала в цепочку b; если нетерминал B встречается более одного раза, для указания соответствия используются верхние целочисленные индексы;
S — начальный символ, выделенный нетерминал из N.
Определим выводимую пару (аналог сентенц.формы) в схеме Tr следующим образом:
(1) (S, S) — выводимая пара, в которой символы S соответствуют друг другу;
(2) если (aAb; a'Ab') — выводимая пара, в цепочках которой вхождения A соответствуют друг другу, и A ® g,g’ — правило из R, то (agb; a'g'b') — выводимая пара.
Для обозначения такого вывода одной пары из другой будем пользоваться обозначением Þ: (aAb, a'Ab') Þ (agb, a'g'b'). Рефлексивно-транзитивное замыкание отн-я Þ обозначим Þ*.
Переводом τ(Tr), определяемым СУ-схемой Tr, назовем множество пар
{(x, y) | (S, S)Þ*(x, y), x ÎS*, y ÎD*}.
СУ-схема Tr = (N, S, D, R, S) называется простой, если для каждого правила A ® a, b из R соответствующие друг другу вхождения нетерминалов встречаются в a и b в одном и том же порядке.
Перевод, определяемый простой СУ-схемой, называется простым синтаксически управляемым переводом (простым СУ-переводом).
Имея дерево вывода для входной цепочки (полученное ранее (с помощью МПА)), применяем к нему правые части правил СУ-схемы и получаем выходную цепочку. Т.о. СУ-сехма — это алгоритм.
Пример (Польская запись: инфиксная форма ® префиксная):
E ® T, T
E ® T+E, +TE
T ® F, F
T ® F*T, +FT
F ® a, a
F ® b, b
F ® (E), E
Для префиксной формы $ и более простая однозначная грамматика:
E ® +EE
E ® *EE
E ® a
E ® b
Пример ((суффиксная) польская запись ® алгоритм на Assembler’е):
E ® EE+
E ® EE*
E ® a
E ® b
Добавим нетерминал I и стартовый:
E ® EE+,
E ® EE*,
E ® I,
I ® a,
I ® b,
S ® IE=,
Команды ассемблера:
load, store — загрузить, сохранить в памяти;
push, pop — загрузить из аккумулятора в стек, из стека в аккумулятор;
addsp, mulsp — сложить/умножить то, что в аккумуляторе, с верхушкой стека;
$ — разделитель строк, команд.
Аккумулятор — фактически регистр.
E ® E(I)E(II)+, E(I)E(II) pop $ addsp $ push $
E ® E(I)E(II)*, E(I)E(II) pop $ mulsp $ push $
E ® I, I
I ® a, a
I ® b, b
S ® IE=, E pop $ store I $
Методы системного программирования:



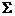 ,
, 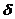 , S, F), где
, S, F), где r(Q) — функция переходов (отображающая множество
r(Q) — функция переходов (отображающая множество 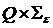 во множество подмножеств множества Q), определяющая поведение управляющего устройства,
во множество подмножеств множества Q), определяющая поведение управляющего устройства,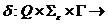 r (Q´Г*) — ф-я переходов ( r (Q´Г*) — мн-во конечных подмн-в
r (Q´Г*) — ф-я переходов ( r (Q´Г*) — мн-во конечных подмн-в 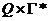 );
);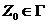 — маркер дна, символ, находящийся в магазине в начальный момент (начальный символ магазина);
— маркер дна, символ, находящийся в магазине в начальный момент (начальный символ магазина);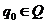 — начальное сост-е (напишем q0 или S — разницы нет, общность не нарушается);
— начальное сост-е (напишем q0 или S — разницы нет, общность не нарушается); — -/-/-.
— -/-/-. — текущее состояние управляющего устройства;
— текущее состояние управляющего устройства; — непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой (если w =
— непрочитанная часть входной цепочки; первый символ цепочки w находится под входной головкой (если w = 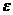 , то считается, что вся входная лента прочитана);
, то считается, что вся входная лента прочитана);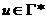 — содержимое магазина (если u =
— содержимое магазина (если u = 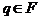 (т.е. управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана).
(т.е. управляющее устройство находится в одном из заключительных состояний, а входная цепочка целиком прочитана).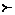 , определенного на конфигурациях:
, определенного на конфигурациях: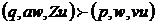 , если множество d(q, a, Z) содержит (p, v), где
, если множество d(q, a, Z) содержит (p, v), где 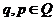 ,
, 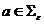 ,
, 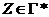 и
и 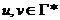 (если верхушка магазина слева).
(если верхушка магазина слева).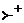 ,
, 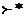 и
и 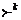 — транзитивное и рефлексивно-транзитивное замыкание отношения
— транзитивное и рефлексивно-транзитивное замыкание отношения 
 (разница в *) во множество конечных подмножеств множества
(разница в *) во множество конечных подмножеств множества 



