

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Для определения сложности алгоритма рассмотрим входные данные размера n.
Сложность – это кол-во шагов (эл.операций) алгоритма в худшем случае по всем входным данным. Сложность зависит от размера входных данных и их представления. Наибольший интерес представляет поведение функции при больших n.
f(n) = O(g(n)).
Если существуют с и N такие, что f(n) <= c*g(n), для 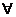 n > N, т.е. g(n) растет быстрее, чем f(n).
n > N, т.е. g(n) растет быстрее, чем f(n).
g(n) – функция от размера входных данных, характеризующая рост сложности алгоритма. Сложность может расти полиноминально, экспоненциально.
Полиномиальные алгоритмы являются практически полезными для вычислительной задачи относительно экспоненциальных, которые при росте входных данных быстрее перестают быть применимыми.
Индивидуальная задача - задача с конкретными данными.
Задача распознавания – для индивидуальной задачи и заданной константы L найти ответ на вопрос существует ли решение, стоимость которого не больше (не меньше) заданной границы L.
Класс Р - класс задач распознавания, которые могут быть решены некоторым полиномиальным алгоритмом.
Для того чтобы задача содержалась в классе NP, мы не требуем, чтобы ответ в каждой индивидуальной задаче мог быть получен за полиномиальное время с помощью некоторого алгоритма. Мы требуем просто, чтобы в том случае, когда в индивидуальной задаче х ответ был да, существовало бы краткое (т. е. с длиной, ограниченной полиномом от размера х) удостоверение для х, справедливость которого можно было бы проверить за полиномиальное время.
Примеры задач класса NP:
1. КЛИКА – подграф в котором каждая вершина связана с каждой.
Задача распознавания: для графа и числа L нужно определить существует ли в графе клика с величиной размера L.
|
|
Удостоверение: сама клика, док-во удостоверения: проверка, что каждая вершина в клике связана с каждой.
КОМИВОЯЖЕР.
Задача распознавания: для графа и числа L нужно определить существует ли в графе обход <= L.
Удостоверение: сам обход, док-во удостоверения: определить является ли это обходом и его длина <= L.
ВЫПОЛНИМОСТЬ.
Задача распознавания: для даной формулы определить может ли она быть истинной для какого-либо набора переменных.
Удостоверение: может служить набор значений истинности.
Док-во удостоверения: будет просто проверять, что формула истинная на данном наборе значений.
Дополнение задачи коммивояжера: определить, что в данном графе нет обходов меньше L. Эта задача не относиться к классу NP, т.е. перебрать все существующие обходы и доказать, что они меньше L, нельзя за полиномиальное время.
Если задача распознавания относится к NP, то сама индивидуальная задача называется NP-трудной.
Задача называется NP-полной, если она принадлежит к классу NP и любая задача из NP полиномиально сводиться к ней.
Пусть А1 и А2— задачи распознавания. Будем говорить, что А1 сводится за полиномиальное время к А2 тогда и только тогда, когда существует полиномиальный алгоритм А1 для А1, использующий несколько раз в качестве подпрограммы с единичной стоимостью алгоритм A 2 для А2.
Теорема Кука: задача о выполнимости является NP полной.
Еще ряд задач из NP(Клика и ЗК) являются NP- полными, для доказательства этого рассматриваемую задачу преобразуют в задачу ВЫПОЛНИМОСТЬ или какую-нибудь другую задачу, NP-полнота которой уже доказана.
35) Метод ветвей и границ (на примере задачи коммивояжёра).
Задача коммивояжера - задача дискретной оптимизации. Решение этой задачи конечно, но полный перебор в большинстве случаев не возможен. МВГ один из способов сокращения перебора. Но этот алгоритм эвристический, т.е. сокращение перебора не гарантируется. Мн-во всех решений делится на части. Отсекаем мн-ва, в которых скорее всего не будет оптимального решения. Сначала мы выбираем ребра с минимальным весом. Потом мы выбираем разделяющие элементы, те которые при удалении из обхода дают нам самое максимальное увеличение стоимости. Так как мы выбрали одно ребро, размерность задачи уменьшилась на единицу. Делаем это до тех пор, пока размерность не станет на столько маленькой, что можно применить перебор.
|
|
Алгоритм Литтла:
Дана матрица расстояний. Необходимо с помощью алгоритма Литтла решить задачу коммивояжера.

1) Справа к таблице присоединяем столбец Ui, в котором записываем минимальные элементы соответствующих строк. Вычитаем элементы Ui из соответствующих элементов строки матрицы.

2) Внизу полученной матрицы присоединяем строку Vj, в которой записываем минимальные элементы столбцов. Вычитаем элементы Vj из соответствующих столбцов матрицы.

3) В результате вычислений получаем матрицу, приведенную по строкам и столбцам.
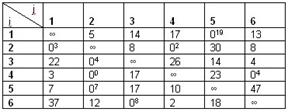
4) Находим константу приведения:  . Таким образом, нижней границей множества всех гамильтоновых контуров будет число
. Таким образом, нижней границей множества всех гамильтоновых контуров будет число 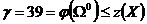 .
.
5) Находим степени нулей полностью приведенной матрицы. Для этого как бы заменяем в ней все нули на знак «∞» и устанавливаем сумму минимальных элементов соответствующей строки и столбца. Степени нулей записаны в правых верхних углах клеток, для которых  .
.
6) Определяем максимальную степень нуля. Она равна 19 и соответствует клетке (1;5). Таким образом, претендентом на включение в гамильтонов контур является дуга (1;5).
7) Разбиваем множество всех гамильтоновых контуров  на два:
на два: 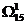 и
и 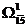 . Матрицу
. Матрицу 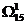 с дугой (1;5) получаем путем вычеркивания строки 1 и столбца 5 из матрицы, приведенной по столбцам и строкам. Чтобы не допускать образования не гамильтонова контура, заменяем элемент (5;1) на знак «∞».
с дугой (1;5) получаем путем вычеркивания строки 1 и столбца 5 из матрицы, приведенной по столбцам и строкам. Чтобы не допускать образования не гамильтонова контура, заменяем элемент (5;1) на знак «∞».
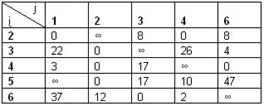
8) Матрицу гамильтоновых контуров 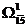 получим путем замены элемента (1;5) на знак ∞ в матрице, приведенной по столбцам и строкам.
получим путем замены элемента (1;5) на знак ∞ в матрице, приведенной по столбцам и строкам.

9) Делаем дополнительное приведение матрицы контуров 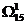 :
:  = 0. Нижняя граница множества
= 0. Нижняя граница множества 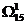 равна
равна 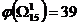 .
.
10) Находим константу приведения для множества контуров 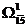 :
:  . Следовательно, нижняя граница множества
. Следовательно, нижняя граница множества 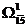 равна
равна 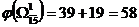 .
.
11) Сравниваем нижние границы подмножеств 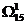 и
и 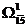 . Так как
. Так как 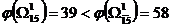 , то дальнейшему ветвлению подвергаем множество
, то дальнейшему ветвлению подвергаем множество 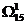 . На рисунке представлено ветвление по дуге (1;5):
. На рисунке представлено ветвление по дуге (1;5):
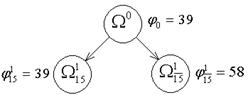
Переходим к ветвлению подмножества 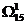 . Его приведенная матрица представлена в таблице ниже.
. Его приведенная матрица представлена в таблице ниже.
|
|

12) Узнаем степени нулей матрицы. Претендентами на включение в гамильтонов контур будут несколько дуг (5;2) и (6;3). Для дальнейших расчетов выберем дугу (6;3). Разбиваем множество 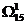 на два подмножества:
на два подмножества:  и
и 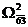 (табл. 3 и 4). Чтобы не допустить образования не гамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞»
(табл. 3 и 4). Чтобы не допустить образования не гамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞»
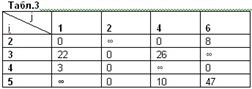

Определим константы приведения для этих матриц 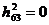 ,
, 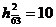 . Следовательно,
. Следовательно, 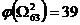 ,
,  . Так как
. Так как 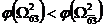 , то дальнейшему ветвлению подлежит подмножество
, то дальнейшему ветвлению подлежит подмножество  . Находим степени нулей матрицы.
. Находим степени нулей матрицы.
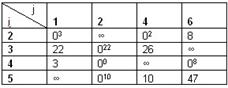
Претендентом к включению в гамильтонов контур станет дуга (3;2). Разбиваем множество  на два
на два 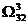 и
и 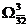 .
.

Очевидно, 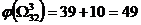 ,
, 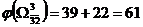 . Следовательно, очередному ветвлению нужно подвергнуть подмножество
. Следовательно, очередному ветвлению нужно подвергнуть подмножество 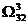 .
.
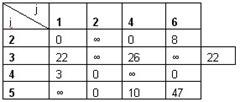
Переходим к ветвлению подмножества 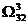 . Его приведенная матрица представлена в таблице ниже.
. Его приведенная матрица представлена в таблице ниже.
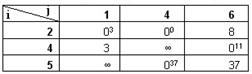
Определяем степени нулей. Претендентом на включение в гамильтонов контур является дуга (5;4). Разбиваем множество 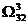 на два подмножества:
на два подмножества: 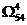 и
и  .
.
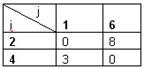
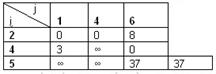
Находим нижние границы 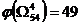 ,
, 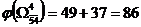 . Следовательно, очередному ветвлению нужно подвергнуть подмножество
. Следовательно, очередному ветвлению нужно подвергнуть подмножество 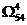 . Но его матрица имеет размерность
. Но его матрица имеет размерность 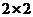 . Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице
. Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице 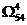 нулевым элементам. Это дуги (2;1) и (4;6). На рисунке ниже представлено дерево ветвлений. Определим полученный гамильтонов контур. В него вошли дуги
нулевым элементам. Это дуги (2;1) и (4;6). На рисунке ниже представлено дерево ветвлений. Определим полученный гамильтонов контур. В него вошли дуги  . Длина контура равна
. Длина контура равна 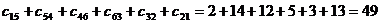 . Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.
. Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.
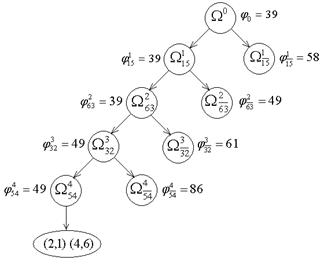

Буква X обозначает текущую вершину на дереве поиска, w(X) – соответствующую нижнюю границу. Вершины, следующие непосредственно за X, назовем Y и 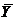 ; они выбираются ветвлением по некоторому ребру (k, l). Символ z0 обозначает стоимость самого дешевого тура, известного на данный момент. В начальный момент z0 = ∞.
; они выбираются ветвлением по некоторому ребру (k, l). Символ z0 обозначает стоимость самого дешевого тура, известного на данный момент. В начальный момент z0 = ∞.
Блок 1. Установление начальных значений переменных, или инициализация.
Блок 2. Первое приведение – это непосредственная реализация описанной ранее процедуры.
Блок 3. Выбор следующего ребра ветвления (k, l) определяет множества Y и 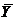 , непосредственно следующие за X. Ребро (k, l) нужно выбирать так, чтобы попытаться получить большую по величине нижнюю границу на множестве
, непосредственно следующие за X. Ребро (k, l) нужно выбирать так, чтобы попытаться получить большую по величине нижнюю границу на множестве 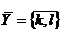 , что облегчит проведение оценки для множества
, что облегчит проведение оценки для множества 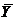 .
.
|
|
Блок 4. Определяем вершину 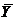 , следующую за X, точно так же, как мы делали раньше.
, следующую за X, точно так же, как мы делали раньше.
Блок 5. Вершине Y, следующей за X, соответствует подмножество туров из X, содержащих то ребро (k, l) в блоке 3.
Блок 6. В конце концов мы должны прийти к множествам, содержащим так мало туров, что мы можем рассмотреть каждый их них и провести оценку для этой вершины без дальнейшего ветвления.
Блок 7 и 8. Блок 7 работает, только если С – матрица размеров 2×2. В этом блоке отыскивается самый дешевый тур в Y и его вес обозначается через w(Y). В блоке 8 проверяется, лучше ли данный тур, чем текущий лучший из известных туров. Если нет, то новый тур отбрасывается. Если да, то текущим лучшим туром становится новый тур, и мы полагаем z0= w(Y).
Блок 9. Теперь нужно выбрать следующую вершину X, от которой проводить ветвление. Выбираем вершину, из которой в данный момент не выходят ветви и которая имеет наименьшую границу.
Блок 10. Если текущая граница для наилучшего тура z0 меньше или равна w(X) – наименьший из неисследованных нижних границ, - тогда никакая из вершин, следующих за X, не может содержать лучшего тура.
Блок 11. В этой части алгоритма получается откорректированная матрица стоимостей С для текущей вершины X.
Принципы ООП. Конструкторы. Таблица виртуальных методов. Раннее и позднее связывание.
Объектно-ориентированное программирование основано на «трех китах» - трех важнейших принципах, придающих объектам новые свойства:
1. Инкапсуляция. Инкапсуляция есть объединение в единое целое данных и алгоритмов обработки этих данных. В рамках ООП данные называются полями объекта, а алгоритмы - объектными методами. Инкапсуляция позволяет в максимальной степени изолировать объект от внешнего окружения. Она существенно повышает надежность разрабатываемых программ, т.к. локализованные в объекте алгоритмы обмениваются с программой сравнительно небольшими объемами данных, причем количество и тип этих данных обычно тщательно контролируются. В результате замена или модификация алгоритмов и данных, инкапсулированных в объект, как правило, не влечет за собой плохо прослеживаемых последствий для программы в целом (в целях повышения защищенности программ в ООП почти не используются глобальные переменные). Другим немаловажным следствием инкапсуляции является легкость обмена объектами, переноса их из одной программы в другую.
2. Наследование. Наследование есть свойство объектов порождать своих потомков. Объект-потомок автоматически наследует от родителя все поля и методы, может дополнять объекты новыми полями и заменять (перекрывать) методы родителя или дополнять их. Принцип наследования решает проблему модификации свойств объекта и придает ООП в целом исключительную гибкость. При работе с объектами программист обычно подбирает объект, наиболее близкий по своим свойствам для решения конкретной задачи, и создает одного или нескольких потомков от него, которые «умеют» делать то, что не реализовано в родителе.
|
|
3. Полиморфизм. Полиморфизм - это свойство родственных объектов (т.е. объектов, имеющих одного общего родителя) решать схожие по смыслу проблемы разными способами. В рамках ООП поведенческие свойства объекта определяются набором входящих в него методов. Изменяя алгоритм того или иного метода в потомках объекта, программист может придавать этим потомкам отсутствующие у родителя специфические свойства. Для изменения метода необходимо перекрыть его в потомке, т.е. объявить в потомке одноименный метод и реализовать в нем нужные действия. В результате в объекте-родителе и объекте-потомке будут действовать два одноименных метода, имеющие разную алгоритмическую основу и, следовательно, придающие объектам разные свойства. Это и называется полиморфизмом объектов.
Конструктор. В объектно-ориентированном программировании конструктор класса — специальный блок инструкций, предназначенный для инициализации объекта и вызываемый автоматически при создании объекта.
· Конструктор не возвращает значение.
· Класс может иметь несколько конструкторов с разными параметрами для разных видов инициализации.
· Конструктор, вызываемый без параметров, называется конструктором по умолчанию.
· Если программист не указал ни одного конструктора, то компилятор создает его автоматически.
· Конструкторы не наследуются.
· Конструктор не может быть виртуальным, т.к. в момент создания у объекта нет таблицы виртуальных функций.
Виртуальный метод (виртуальная функция) — в объектно-ориентированном программировании метод класса, который может быть переопределён в классах-наследниках так, что конкретная реализация метода для вызова будет определяться во время исполнения. Таким образом, программисту необязательно знать точный тип объекта для работы с ним через виртуальные методы: достаточно лишь знать, что объект принадлежит классу или наследнику класса, в котором метод объявлен.
Виртуальные методы — один из важнейших приёмов реализации полиморфизма. Они позволяют создавать общий код, который может работать как с объектами базового класса, так и с объектами любого его класса-наследника. При этом базовый класс определяет способ работы с объектами и любые его наследники могут предоставлять конкретную реализацию этого способа. В некоторых языках программирования, например в Java (там все методы виртуальные по умолчанию), нет понятия виртуального метода, данное понятие следует применять лишь для языков, в которых методы родительского класса не могут быть переопределены по умолчанию, а только с помощью некоторых вспомогательных ключевых слов.
Базовый класс может и не предоставлять реализации виртуального метода, а только декларировать его существование. Такие методы без реализации называются «чисто виртуальными» или абстрактными. Класс, содержащий хотя бы один такой метод, тоже будет абстрактным. Объект такого класса создать нельзя (в некоторых языках допускается, но вызов абстрактного метода приведёт к ошибке). Наследники абстрактного класса должны предоставить реализацию для всех его абстрактных методов, иначе они, в свою очередь, будут абстрактными классами.
Для каждого класса, имеющего хотя бы один виртуальный метод, создаётся таблица виртуальных методов. Каждый объект хранит указатель на таблицу своего класса в скрытом поле. Оно заполняется конструктором при создании объекта. Для вызова виртуального метода используется такой механизм: из объекта берётся указатель на соответствующую таблицу виртуальных методов, а из неё берётся указатель на реализацию метода, используемого для данного класса.
|
|
|

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!