Любая матричная игра имеет решение в смешанных стратегиях, т. е. существует цена игры в смешанных стратегиях V и оптимальные смешанные стратегии P0 и Q0 соответственно игроков А и В, т. е. V= V =maxα(P)= V(верх)= min ß(Q)= α(P0)=ß(Q0)=F(P0, Q0)
Определение седловой точки: пусть задана функция выигрыша F(P,Q) действительная функция из P?SA,Q?SB, точка (P0,Q0) – седловая точка P0?SA,Q0?SB если F(P,Q0)≤ F(P0,Q0)≤ F(P0,Q) для любого P0?SA, Q0?SB
левая часть: max функции F(P,Q0) достигается в точке (P0,Q0), то есть max F(P,Q0)= F(P0,Q0)
правая: min функции F(P0,Q) достигается в точке (P0,Q0), то есть min F(P0,Q)= F(P0,Q0)
max F(P,Q0)= F(P0,Q0)=min F(P0,Q) Это и означает существование седловой точки функции 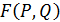 .
.
Рассмотрим для антогонистической игры для чистых стратегий: элемент матрицы aij – седловая точка, если minmax aij=maxmin aij= aij = гамма
16. Аналитическое решение игры 2×2 в смешанных стратегиях.
Пусть матрица А размером 2*2 не имеет седловой точки, т.е. решения в чистых стратегиях. Тогда каждый из игроков 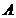 и
и 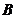 обладает единственной оптимальной смешанной стратегией соответственно P*=(p1*,p2*) и Q*=( q1*,q2* ), где
обладает единственной оптимальной смешанной стратегией соответственно P*=(p1*,p2*) и Q*=( q1*,q2* ), где
p1*=(а22-а21)/(а11+а22-а12-а21)
p2*=(а22-а12)/(а11+а22-а12-а21)
v = (а22*а11-а12*а21)/(а11+а22-а12-а21)
q1*=(а22-а12)/(а11+а22-а12-а21)
q2*=(а11-а21)/(а11+а22-а12-а21)
Рассмотрим функцию выигрыша игрока A более подробно: F(P,Q)=∑∑piaijqj
(P, Q)? SA*SB
Примем также следующие обозначения:
p=p1, p2=1-p
q=q1, q2=1-q
Пусть m=2 и n=2,
тогда F(P,Q)=p(qa11+(1-q)a12)+(1-p)(qa21+(1-q)a22)
Представим в явном виде функцию 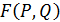 как линейную функцию с аргументом (независимой переменной) q. Получим следующее выражение:
как линейную функцию с аргументом (независимой переменной) q. Получим следующее выражение:
F(P,Q)=(a22+p(a12-a22))+q(p(a11-a12-a21+a22)+(a21-a22))
Если
p(a11-a12-a21+a22)+(a21-a22)>0, т.е. если
p>(a22-a21)/(a11-a12-a21+a22), график функции имеет положительный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать свои потери (минимизировать функцию), выбирая свою второю чистую стратегию, т.е. реализуя смешанную стратегию Q=(0;1),q=0. В итоге исход игры определится результатом гамма= F(P0,Q0)=a22+p(a12-a22)
Если p(a11-a12-a21+a22)+(a21-a22)<0, т.е. если
p<(a22-a21)/(a11-a12-a21+a22),, график функции имеет отрицательный наклон. Это значит, что в ответ на действия игрока A игрок B будем минимизировать функцию, выбирая свою первую чистую стратегию Q=(1;0),q=1
Т. о.
а21+р(а11-а21)=ра11+(1-р)а21=а11р1+а21р2=v
a22+p(a12-a22)=pa12+(1-p)a22=p1*a12+p2a22=V
p1+p2=1
a11 p1*+a21 p*2 = v.
a12 p1*+a22 p*2 = v
p1*+ p*2=1
Решая эту систему, получим оптимальную стратегию
p1*=(а22-а21)/(а11+а22-а12-а21)
p2*=(а22-а12)/(а11+а22-а12-а21)
и цену игры v = (а22*а11-а12*а21)/(а11+а22-а12-а21)
средний проигрыш второго игрока равен v, т.е. a11 q1*+ a12 q2*=v.
Тогда оптимальная стратегия второго игрока определяется по формулам:
q1*=(а22-а12)/(а11+а22-а12-а21)
q2*=(а11-а21)/(а11+а22-а12-а21)
17. Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока A.
Составим систему уравнений на основе матрицы:
A11 a12
A21 a22
a11 p1+a21 p2 = v.
a12 p1+a22 p2 = v
p1+ p2=1
рассмотрим первое уравнение: a11 p1+a21 p2 = v.
a11 p1+a21 (1-p1) = v.
а21+p1(а11-а21)=V
если р=0 V=a21
p=1 V=a11
аналогично для второго уравнения
Итак, мы можем сформулировать общий алгоритм геометрического нахождения оптимальных стратегий игрока А, цены игры, нижней и верхней цены игры в чистых стратегиях, седловых точек матрицы и доминирующих стратегий игроков.
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый соответ. стратегии А1 и правый, соотв.стратегии А2.
3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) элементы a11 и a12 первой строки матрицы А
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] (как на вертикальной числовой оси) элементы a21 и a22 второй строки матрицы А
5. Соединяем точки, изображающие элементы с одинаковыми вторыми индексами, т.е. эл-ты, стоящие в одном и том же столбце матрицы А: a11 с a21 и a12 с a22. В результате получаем отрезки a11a21 и a12a22.
6. Находим нижнюю огибающую отрезков a11a21 и a12a22
7. Находим наивысшие точки нижней огибающей
8. Проектируем их ортогонально на горизонтальный отрезок [0,1]
9. Полученные проекции р0 определяют оптимальные стратегии Р0=(1-р0,р0) игрока А.
10. Ордината наивысшей точки огибающей равна цене игры V
11. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях 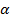
12. Нижний из двух верхних концов отрезков a11a21 и a12a22 есть верхняя цена игры в чистых стратегиях 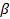
13. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка a11a21 или a12a22, на котором он лежит, то этот эл-т является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
Если матрица игры содержит седловую точку, то автоматически выявляется и оптимальная стратегия игрока В. Но можно достаточно удовлетворительно проинтерпретировать геометрически оптимальную стратегию игрока В и в случае отсутствия седловых точек.
18. Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока B.
Составим систему уравнений на основе матрицы:
A11 a12
A21 a22
a11 q1+a12 q2 = v.
a21 q1+a22 q2 = v
q1+ q2=1
рассмотрим первое уравнение: a11 q1+a12 q2 = v.
a11 q1+a12 (1-q1)= v.
а12+q1(а11-а12)=V
если q=0 V=a12
q=1 V=a11
аналогично для второго уравнения
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый соответ. стратегии А1 и правый, соотв.стратегии А2.
3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) элементы a11 и a21 первого столбца матрицы А
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] (как на вертикальной числовой оси) элементы a12 и a22 второго столбца матрицы А
5. Соединяем точки, изображающие элементы с одинаковыми первыми индексами, т.е. эл-ты, стоящие в одной и той же строке матрицы А: a11 с a12 и a21 с a22. В результате получаем отрезки a11a12 и a21a22.
6. Находим верхнюю огибающую отрезков a11a12 и a21a22.
7. Находим низшие точки верхней огибающей
8. Проектируем их ортогонально на горизонтальный отрезок [0,1]
9. Полученные проекции q0 определяют оптимальные стратегии Q0=(1-q0,q0)игрока B.
10. Ордината низшей точки огибающей равна цене игры V
11. нижний из двух концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях ß
12. верхний из двух нижних концов отрезков есть нижняя цена игры в чистых стратегиях
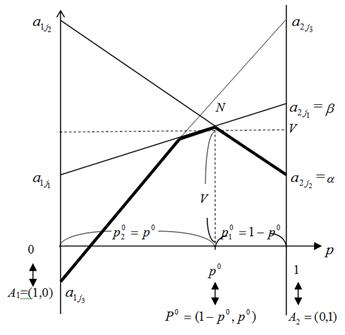
19. Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока A.
Решение игр размера 2xn или nx2 допускает наглядную геометрическую интерпретацию.
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый и правый
3. На левом перпендикуляре вертикальной числовой оси от точки 0 его пересечения с отрезком [0,1] откладываем все элементы матрицы А стоящих в 1 строке
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все эл-ты матрицы А второй строки
5. Каждую пару точек, изображающих элементы a1j a2j j=1,…,n, стоящие в j ом столбце матрицы А, соединяем отрезком a1j a2j. Таким образом будут построены n отрезков, представляющих собой графики n линейных функций
H(P,Bj)=(a2j-a1j)p+a1j, p принадлежит [0.1] j= 1,…,n
6. Находим нижнюю огибающую семейства отрезков (выпуклая вверх ломанная)
7. На нижней огибающей находим максимальную точку
8. Смешанная стратегия Р0=(1-р0, р0) является оптимальной стратегией игрока А.
9. Ордината наивысшей точки нижней огибающей является ценой игры V
10. Верхний из концов нижней огибающей (лежащей на перпендикулярах) есть нижняя цена игры в чистых стратегиях 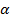
11. Нижний из концов верхней огибающей (лежащий на перпендикулярах) есть верхняя цена игры в чистых стратегиях 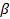
12. Элемент матрицы А, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры.
20. Геометрический метод нахождения цены игры m ×2 и оптимальных стратегий игрока B.
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый и правый
3. На левом перпендикуляре вертикальной числовой оси от точки 0 его пересечения с отрезком [0,1] откладываем все элементы матрицы А стоящих в 1 столбце
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все эл-ты столбца матрицы А стоящих в 2 столбце
5. Каждую пару точек, изображающих элементы ai1 ai2 i=1,…,m, стоящие в i ой строке матрицы А, соединяем отрезком ai1 ai2. Таким образом будут построены m отрезков, представляющих собой графики m линейных функций
H(Ai,Q)=(ai2-ai1)q+ai1, q принадлежит [0.1] i = 1,…,m
6. Находим верхнюю огибающую семейства отрезков (выпуклая вниз ломанная)
7. На верхней огибающей находим минимальную точку
8. Смешанная стратегия Q0=(1-q0, q0) является оптимальной стратегией игрока B.
9. Ордината минимальной точки верхней огибающей является ценой игры V
10. Верхний из концов нижней огибающей (лежащей на перпендикулярах) есть нижняя цена игры в чистых стратегиях 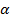
11. Нижний из концов верхней огибающей (лежащий на перпендикулярах) есть верхняя цена игры в чистых стратегиях 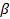
12. Элемент матрицы А, изображающая точка – нижний конец отрезка на котором она лежит и верхним на перпендикуляре будет седловой точкой игры.
21. Доминирование смешанных стратегий для игрока A.
Отыскание решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т.е. сведения данной игры со сложной матрицей к игре с более простой матрице. Рассмотрим один из способов редуцирования игр, основанный на принципе доминирования.
Пусть имеем игру с матрицей m*n
рассмотрим две произвольные стратегии А:
P’= (p’I, p’2,…, p’m)
P’’=(p’’I, p’’2,…, p’’m)
Доминирующая стратегия приносит игроку А выигрыш не меньше, чем другая любая.
Стратегия Р’’доминирует стратегию P’ если
∑p’iai1≤∑p’’iai1
∑p’iain≤∑p’’iain
Или ∑p’iaij≤∑p’’iaij j=1,2,…n.
Поиск доминирующих стратегий:
выпуклая линейная комбинация чистых стратегий игрока A:
λ1А1+ λ2А2+…+ λkАk+…+ λmАm
∑ λi=1 λi≥0
λi аналоги вероятностей рi система ограничений:
λk=0
λ1а1j+ λ2a2j+…+λmamj≥akj
∑ λi=1
Стратегия P=(p1= λ1; p2= λ2; pk=0;…;pm=λm)
признаётся доминирующей стратегию Ak
22. Доминирование смешанных стратегий для игрока В.
Отыскание решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т.е. сведения данной игры со сложной матрицей к игре с более простой матрице. Рассмотрим один из способов редуцирования игр, основанный на принципе доминирования.
Пусть имеем игру с матрицей m*n
рассмотрим две произвольные стратегии B:
Q’= (q’I, q’2,…, q’m)
Q’’=(q’’I, q’’2,…, q’’m)
Стратегия Q’’доминирует стратегию Q’ если
∑q’ja1j≥∑q’’ja1j (средний проигрыш второго игрока в ответ на реализацию игроком А своей 1 стратегии)
∑q’ja2j≥∑q’’ja2j
Или ∑q’jaij≥∑q’’jaij j=1,2,…n.
Доминирующая стратегия приносит игроку В проигрыш не больше, чем другая любая.
Поиск доминирующих стратегий:
выпуклая линейная комбинация чистых стратегий игрока B:
μ1B1+ μ2B2+…+ μkBk+…+ λnBn
∑ μj=1 μj ≥0
μj аналоги вероятностей qj система ограничений:
μk=0
μ1аi1+ μ2ai2+…+ μnain≤aik
∑ μj =1
Стратегия Q=(q1= μ1; q2= μ2; qk=0;…;qn= μn)
признаётся доминирующей стратегию Bk
23. Решение матричной игры m × n сведением к задаче линейного программирования для игрока A.
Решение матричной игры m×n с матрицей А, элементы которой удовлетворяют условию aij>0 i=1,…,m j=1,…,n, эквивалентно решению пары двойственных друг другу стандартных задач линейного программирования:
Найти min ∑xi при ограничениях
xi≥0, i=1,…,m ∑ aij xi≥1 j=1,…,n
Найти max ∑yj при ограничениях
yj≥0, j=1,…n ∑ aij yj≤1 i=1,…,m
точнее говоря, если x0=(x10,…,xm0) и y0=(y10,…,yn0) – оптимальные решения задачи, то V=(∑ xi0)-1=(∑ yj0)-1 – цена игры с матрицей А, P0=Vx0=(p01= Vx01,…,pm0= Vx0m)- оптимальная стратегия игрока А, Q0=Vy0=(q01= Vy01,…,qn0= Vy0n) - оптимальная стратегия игрока B,
Необходимо определить оптимальные стратегии P0=(p10,p20,…,pm0) и Q0=(q10,q20,…,qn0), где ∑ pi0 =1, ∑ qj0 =1
Если игрок A применяет смешанную стратегию P0=(p1,p2,…,pm) против любой чистой стратегии Bj игрока B, то он получает средний выигрыш
F(P,Bj)=a1j*p1+a2j*p2+…+amj*pm
В соответствии с теоремой фон Неймана, в любой антагонистической игре существует решение в смешанных стратегиях, т.е. для игрока A существует оптимальная стратегия P0и соответствующий ей оптимальный выигрыш  .
.
Для оптимальной стратегии P0 все средние выигрыши F(P,Bj) не меньше цены игры  , поэтому получаем систему неравенств:
, поэтому получаем систему неравенств:
a11*p1+a21*p2+…+am1*pm≥V
a1n*p1+a2n*p2+…+amn*pm≥V
x1=p1/V xm=pm/V при V>0
Если величинаV≤0, неравенства можно преобразовать, поменяв игроков ролями и изменив у всех элементов матрицы знак на противоположный.
a11*x1+a21*x2+…+am1*xm≥1
a1n*x1+a2n*x2+…+amn*xm≥1
x1+x2+..+xm=1/V
Цель игрока A – максимизировать свой гарантированный выигрыш, т.е. максимизировать цену игры V. Максимизация цены игры V эквивалентна минимизации величины1/V. Поэтому задача поиска оптимальной стратегии P0для игрока A может быть сформулирована следующим образом:
x1+x2+..+xm→min
a11*x1+a21*x2+…+am1*xm≥1
a1n*x1+a2n*x2+…+amn*xm≥1
xi≥0
P0=(p10=x10*V, p20=x20*V,…, pm0=xm0*V)
V=1/(x10+x20+…+xm0)
Пример:
Приведем к матрице с положительными элементами, прибавив к каждому ее элементу число, больше макисмального модуля отрицательных элементов матрицы. В данном случае 3>max {│-2│, │-1│}.
Найти минимум целевой функции f(x1, x2, x3)= x1+ x2+ x3
x1>0, x2>0, x3>0
x1+6 x2+5 x3≥1
4 x1+ x2+5 x3≥1
4 x1+6 x2+2 x3≥1
24. Решение матричной игры m × n сведением к задаче линейного программирования для игрока B.
Решение матричной игры m×n с матрицей А, элементы которой удовлетворяют условию aij>0 i=1,…,m j=1,…,n, эквивалентно решению пары двойственных друг другу стандартных задач линейного программирования:
Найти min ∑xi при ограничениях
xi≥0, i=1,…,m ∑ aij xi≥1 j=1,…,n
Найти max ∑yj при ограничениях
yj≥0, j=1,…n ∑ aij yj≤1 i=1,…,m
точнее говоря, если x0=(x10,…,xm0) и y0=(y10,…,yn0) – оптимальные решения задачи, то V=(∑ xi0)-1=(∑ yj0)-1 – цена игры с матрицей А, P0=Vx0=(p01= Vx01,…,pm0= Vx0m)- оптимальная стратегия игрока А, Q0=Vy0=(q01= Vy01,…,qn0= Vy0n) - оптимальная стратегия игрока B,
Если игрок B применяет смешанную стратегию Q0=(q1,q2,…,qn) против любой чистой стратегии Ai игрока A, то он получает средний проигрыш
F(Ai,Q)=ai1*q1+ai2*q2+…+ain*qn
∑qj=1.
Для оптимальной стратегии Q0 все средние проигрыши не больше цены игры 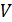 , поэтому получаем систему неравенств:
, поэтому получаем систему неравенств:
a11*q1+a12*q2+…+a1n*qn≤V
am1*q1+am2*q2+…+amn*qn≤V
y1=q1/V yn=qn/V при V>0
y1+y2+..+yn=1/V
Цель игрока B – минимизировать свой гарантированный проигрыш, т.е. минимизировать цену игры V. Минимизация цены игры 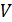 эквивалентна максимизации величины 1/V. Поэтому задача поиска оптимальной стратегии Q0 для игрока B может быть сформулирована следующим образом:
эквивалентна максимизации величины 1/V. Поэтому задача поиска оптимальной стратегии Q0 для игрока B может быть сформулирована следующим образом:
y1+y2+..+yn→max
a11*y1+a12*y2+…+a1n*yn≤1
am1*y1+am2*y2+…+amn*yn≤1
yj≥0
Q0=(q10=y10*V, q20=y20*V,…, qn0=yn0*V)
V=1/(y10+y20+…+yn0)
Пример:
Приведем к матрице с положительными элементами, прибавив к каждому ее элементу число, больше макисмального модуля отрицательных элементов матрицы. В данном случае 3>max {│-2│, │-1│}.
Найти максимум целевой функции φ(y1, y2, y3)= y1+ y2+ y3
y1>0, y2>0, y3>0
y1+4 y2+4 y3≤1
6y1+ y2+6y3≤1
5y1+5y2+2y3≤1
25. Основные понятия и определения теории игр с природой.
В игре с природой действуют 2 игрока, только один из которых действует осознанно – этого игрока называют лицом, принимающего решение (А). природа – второй участник игры не является ни союзником, ни противником игрока А, так как природа как сторона игры не действует осознанно злономеренно против игрока А, а принимает случайным образом одно из своих возможных состояний, не преследуя никаких конкретных целей. при этом игрок А не оказывает никакого влияния на состояние природы. В любой момент времени природа может находиться в одном состоянии. Множество состояний природы Sn={П1,П2,Пn}. Совокупность состояний природы формируется либо на основе имеющегося опыта, либо в результате предположений экспертов.
множество стратегий игрока A: SA={S1,S2, Sm}
vij- результат реализации стратегии активного игрока А при j состоянии природы.
Показателем благоприятности состояния Пj природы П для увеличения выигрыша называется наибольший выигрыш при этом состоянии, то есть наибольший элемент в j-ом столбце: ßj=max vij.
Риском rij игрока А при выборе им стратегии Аi в условиях состояния Пjприроды П называется разность между показателем благоприятности 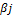 состояния природы природы Пj и выигрышем vij, т.е. разность между выигрышем, который игрок А получил бы, если бы знал заранее, что природа примет состояние Пj, и выигрышем, который он получит при этом же состоянии Пj, выбрав стратегию Аi: rij =
состояния природы природы Пj и выигрышем vij, т.е. разность между выигрышем, который игрок А получил бы, если бы знал заранее, что природа примет состояние Пj, и выигрышем, который он получит при этом же состоянии Пj, выбрав стратегию Аi: rij = 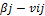 .
.
Таким образом риск rij игрока А при применении им стратегии Аi есть упущенная им возможность максимального выигрыша 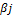 при этом состоянии природы. Эта упущенная возможность определяется как невыигранная часть величины максимального выигрыша.
при этом состоянии природы. Эта упущенная возможность определяется как невыигранная часть величины максимального выигрыша.
Т.е. Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей, а в виде так называемой матрицы рисков или матрицы упущенных возможностей.
rij = 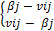 (ГДЕ верхняя строка – матрица выигрышей, нижняя – матрица потерь).
(ГДЕ верхняя строка – матрица выигрышей, нижняя – матрица потерь).
Принятие решений в условиях неопределенности:
Принятие решений в условиях неопределенности основано на том, что вероятности различных вариантов развития событий неизвестны. Принятие решений в условиях риска основано на том, что каждой ситуации развития событий может быть задана вероятность его осуществления.
Байес:
vi0*=max{∑vijqj},
vi0*=min{∑vijqj}
Критерий Лапласа относительно выигрышей (недостаточного основания):
vi0*=max{1/n∑vij}
vi0*=min{1/n∑vij}
Критерий Гермейера
vi0*=max min{ ∑vijqj}
vi0*= min max{ ∑vijqj}
Критерий Ходжа – Лемана
vi0*=max{гамма*∑vijqj+(1-гамма)*minvij},
vi0*=min{гамма*∑vijqj+(1-гамма)*maxvij},
в условиях неопределенности:
Гурвица
vi0*=max{α*max vij+(1-α)*min vij},
vi0*=min{α*min vij+(1-α)*max vij}
Вальда
vi0*=max minvij
vi0*=min maxvij
максимакс
vi0*=max max vij
vi0*=min minvij
Сэвиджа
ri0*=min max rij



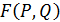 .
.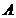 и
и 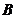 обладает единственной оптимальной смешанной стратегией соответственно P*=(p1*,p2*) и Q*=( q1*,q2* ), где
обладает единственной оптимальной смешанной стратегией соответственно P*=(p1*,p2*) и Q*=( q1*,q2* ), где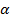
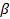




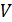 .
.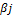 состояния природы природы Пj и выигрышем vij, т.е. разность между выигрышем, который игрок А получил бы, если бы знал заранее, что природа примет состояние Пj, и выигрышем, который он получит при этом же состоянии Пj, выбрав стратегию Аi: rij =
состояния природы природы Пj и выигрышем vij, т.е. разность между выигрышем, который игрок А получил бы, если бы знал заранее, что природа примет состояние Пj, и выигрышем, который он получит при этом же состоянии Пj, выбрав стратегию Аi: rij = 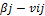 .
.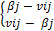 (ГДЕ верхняя строка – матрица выигрышей, нижняя – матрица потерь).
(ГДЕ верхняя строка – матрица выигрышей, нижняя – матрица потерь).


