Рассмотрим следующую игру. Игроки 1 и 2 торгуются о разделе 1 доллара: 1-й игрок предлагает некоторый способ деления, 2-й либо принимает это предложение, либо нет; если нет, то он предлагает способ деления, а 1-й принимает, либо нет и т.д.
Каждое предложение занимает один период, но при этом есть дисконтирующий множитель. Итак, формально рассмотрим следующую трёх-периодную игру.
1.а) В начале первого периода игрок 1 предлагает «свою долю»  доллара, оставляя
доллара, оставляя  игроку 2.
игроку 2.
1.b) Игрок 2 принимает предложение, тогда игра заканчивается, либо отклоняет его. В этом случае игра переходит ко 2-му периоду.
2.a) В начале второго периода игрок 2 предлагает долю 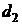 , которую получает игрок 1, оставляя себе
, которую получает игрок 1, оставляя себе  .
.
2.b) Игрок 1 либо принимает предложение, либо нет. В последнем случае игра переходит к 3-му периоду.
3) Игроки в третьем периоде получают доли  ,
, 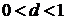 , причём d задан экзогенно.
, причём d задан экзогенно.
Решим данную задачу с помощью обратной индукции. Сначала вычислим, что происходит, если дело доходит до 2-го периода. Игрок 1 может получить d, если отклонит 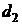 . С учётом дисконтирования (мы сравниваем стоимость в разных (соседних) периодах) игрок 1 примет
. С учётом дисконтирования (мы сравниваем стоимость в разных (соседних) периодах) игрок 1 примет 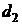 тогда и только тогда, когда
тогда и только тогда, когда  ,
,  – коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением
– коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением  и получением
и получением  в следующем периоде. Дисконтированная стоимость последнего действия есть
в следующем периоде. Дисконтированная стоимость последнего действия есть  , что меньше, чем
, что меньше, чем  , а потому игрок 2 во втором периоде предлагает
, а потому игрок 2 во втором периоде предлагает 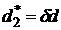 .
.
Таким образом, если игра доходит до второго периода, то 2-й игрок предложит 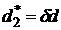 , и игрок 1 примет это предложение.
, и игрок 1 примет это предложение.
Однако игрок 1 может предвидеть, что игрок 2 может получить  во втором периоде, отклоняя предложение
во втором периоде, отклоняя предложение  . В первом периоде стоимость
. В первом периоде стоимость  с учётом дисконтирования составит
с учётом дисконтирования составит  . Значит, игрок 2 принимает
. Значит, игрок 2 принимает  тогда и только тогда, когда
тогда и только тогда, когда  , или
, или  .
.
Поэтому задача игрока 1 в первом периоде состоит в выборе между получением  в этом периоде и получением
в этом периоде и получением 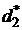 в следующем периоде. Дисконтированная величина
в следующем периоде. Дисконтированная величина 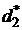 составляет
составляет  , что меньше, чем
, что меньше, чем  . Значит, оптимальное предложение в первом периоде есть
. Значит, оптимальное предложение в первом периоде есть  . Следовательно, в первом периоде игрок 1 предлагает
. Следовательно, в первом периоде игрок 1 предлагает  , а игрок 2 принимает это предложение и получает
, а игрок 2 принимает это предложение и получает  . Таким образом, выигрыш игроков есть
. Таким образом, выигрыш игроков есть  и
и  соответственно.
соответственно.
Модель «инвесторы и банк»
Представим следующую ситуацию. Два инвестора вкладывают по D долларов в банк. Банк инвестировал эти средства в долгосрочный проект. Если форс-мажорные обстоятельства заставляют банк ликвидировать свои инвестиции до того, как проект «созревает», то он покрывает некоторую сумму  , где
, где 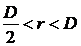 . Если банк позволяет проекту «созреть», то проект принесёт
. Если банк позволяет проекту «созреть», то проект принесёт  ,
,  .
.
Есть два периода, когда вкладчики могут забрать свой вклад: период 1 – до «созревания», период 2 – после созревания. Для упрощения не будем учитывать дисконтирование. Если оба вкладчика забирают вклады в период 1, то оба получают по r и игра заканчивается. Если только один вкладчик забирает в период 1, то он получает D, а второй получает 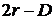 . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает
. Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает 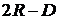 , другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.
, другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.
Дерево игры изображено на рис. 8.16.

Рис. 8.16.
Без строгой формализации игру в период 1 можно изобразить следующим образом:
|
| Забирать
| Не забирать
|
| Забирать
| (r, r)
| (D, 2 r − D)
|
| Не забирать
| (2 r − D, D)
| (Шаг 2)
|
Для периода 2:
|
| Забирать
| Не забирать
|
| Забирать
| (R, R)
| (2 R − D, D)
|
| Не забирать
| (D, 2 R − D)
| (R, R)
|
Рассмотрим внимательно матрицу для периода 2. Поскольку  и
и  , то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:
, то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:
|
| Забирать
| Не забирать
|
| Забирать
| (r, r)
| (D, 2 r − D)
|
| Не забирать
| (2 r − D, D)
| (R, R)
|
Т.к.  и
и  , то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).
, то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).



 доллара, оставляя
доллара, оставляя  игроку 2.
игроку 2.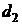 , которую получает игрок 1, оставляя себе
, которую получает игрок 1, оставляя себе  .
. ,
, 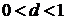 , причём d задан экзогенно.
, причём d задан экзогенно. ,
,  – коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением
– коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением  и получением
и получением  в следующем периоде. Дисконтированная стоимость последнего действия есть
в следующем периоде. Дисконтированная стоимость последнего действия есть  , что меньше, чем
, что меньше, чем  , а потому игрок 2 во втором периоде предлагает
, а потому игрок 2 во втором периоде предлагает 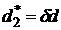 .
. во втором периоде, отклоняя предложение
во втором периоде, отклоняя предложение  . Значит, игрок 2 принимает
. Значит, игрок 2 принимает  , или
, или  .
. в этом периоде и получением
в этом периоде и получением 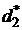 в следующем периоде. Дисконтированная величина
в следующем периоде. Дисконтированная величина  , что меньше, чем
, что меньше, чем  . Следовательно, в первом периоде игрок 1 предлагает
. Следовательно, в первом периоде игрок 1 предлагает  , а игрок 2 принимает это предложение и получает
, а игрок 2 принимает это предложение и получает  . Таким образом, выигрыш игроков есть
. Таким образом, выигрыш игроков есть  и
и  соответственно.
соответственно. , где
, где 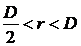 . Если банк позволяет проекту «созреть», то проект принесёт
. Если банк позволяет проекту «созреть», то проект принесёт  ,
,  .
.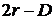 . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает
. Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает 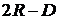 , другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.
, другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.
 , то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:
, то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1: и
и  , то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).
, то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R).


