В одномерном случае производная функции 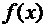 характеризует скорость изменения функции в данной точке в направлении оси
характеризует скорость изменения функции в данной точке в направлении оси 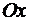 . В двумерном случае частные производные функции
. В двумерном случае частные производные функции 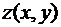 характеризуют то же самое в направлении координатных осей.
характеризуют то же самое в направлении координатных осей.
Естественно поставить вопрос о скорости изменения функции 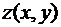 в направлении произвольной оси
в направлении произвольной оси 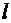 .
.
Пусть функция 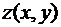 определена в некоторой окрестности точки
определена в некоторой окрестности точки 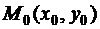 и пусть ось
и пусть ось 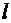 задана углами
задана углами 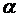 и
и 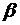 , которые она составляет с осями координат. Ось удобно задавать её ортом:
, которые она составляет с осями координат. Ось удобно задавать её ортом: 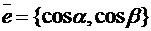 . Будем считать, что ось проходит через точку
. Будем считать, что ось проходит через точку 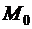 и пусть точка
и пусть точка 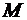 – произвольная точка, лежащая на оси. Тогда
– произвольная точка, лежащая на оси. Тогда 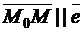 , т.е.
, т.е. 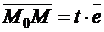 .
.
Определение 1. Пусть точка 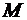 неограниченно приближается к точке
неограниченно приближается к точке 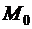 вдоль оси
вдоль оси 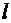 . Предел вида
. Предел вида
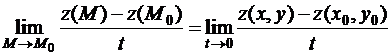 (1)
(1)
называется производной функции 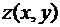 по направлению оси
по направлению оси 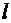 в точке
в точке 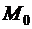 и обозначается одним из символов
и обозначается одним из символов
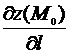 ,
, 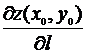 ,
, 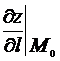 .
.
Теорема 1. Пусть функция 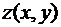 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 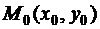 непрерывные частные производные первого порядка и пусть ось
непрерывные частные производные первого порядка и пусть ось 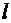 образует с осями координат углы
образует с осями координат углы 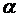 и
и 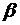 . Тогда производная данной функции по направлению оси
. Тогда производная данной функции по направлению оси 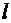 в точке
в точке 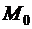 существует и выражается формулой
существует и выражается формулой
 . (2)
. (2)
Доказательство. Пусть 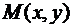 – текущая точка оси
– текущая точка оси 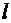 . Так как
. Так как 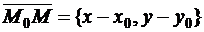 , а
, а 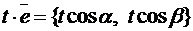 и в силу того, что
и в силу того, что 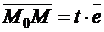 , будем иметь:
, будем иметь:
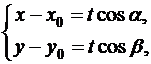
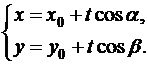
То есть, координаты текущей точки 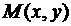 есть функции параметра
есть функции параметра 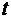 . Тогда:
. Тогда:
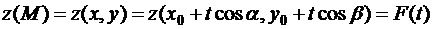 ,
, 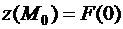
и из (1) имеем:
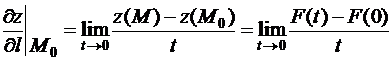 . (3)
. (3)
Последний предел есть производная функции 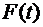 в нуле. Производная же сложной функции
в нуле. Производная же сложной функции 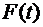 существует, ибо
существует, ибо 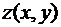 имеет непрерывные производные, а её аргументы
имеет непрерывные производные, а её аргументы 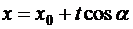 и
и 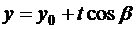 – дифферен-цируемы, при этом:
– дифферен-цируемы, при этом:
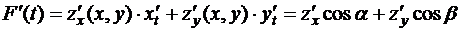 .
.
Рассмотрим последнее равенство при 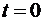 и получим
и получим
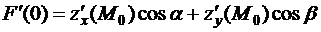 .
.
Теперь формула (3) и доказывает теорему.
Замечание. В случае функции трёх переменных 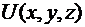 и оси
и оси 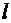 , имеющей орт
, имеющей орт 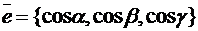 формула (2) приобретает вид
формула (2) приобретает вид
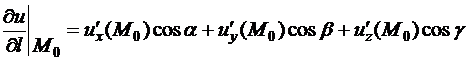 .
.
Пример. Вычислить производную функции 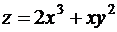 в точке
в точке 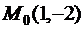 по направлению вектора
по направлению вектора 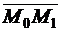 , где
, где 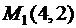 .
.
Решение. Найдём единичный вектор, имеющий данное направление:
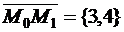 ,
, 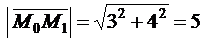 ,
, 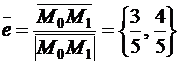 ,
,
откуда 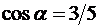 ,
, 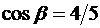 . Далее, вычислим частные производные данной функции в точке
. Далее, вычислим частные производные данной функции в точке 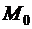 :
: 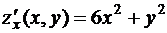 ,
, 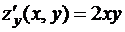 , откуда
, откуда 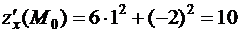 ,
, 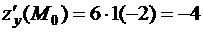 . Теперь по формуле (2) получим
. Теперь по формуле (2) получим
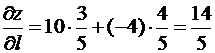 .
.
II Градиент
Определение 2. Вектор, проекциями которого служат частные производные функции 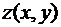 , называется градиентом функции
, называется градиентом функции
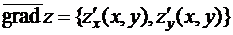 .
.
Для функции трёх переменных 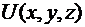 :
:
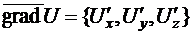 .
.
Связь градиента с производной по направлению даётся следующей теоремой.
Теорема 2. Производная функции по направлению есть проекция её градиента на это направление:
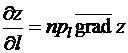 .
.
Доказательство. Проекция вектора на ось – это проекция вектора на орт оси. Проекцию же вектора на вектор можно найти, используя скалярное произведение:
 .
.
Учитывая, что 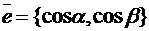 и
и 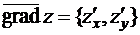 , причём
, причём 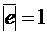 , получим:
, получим:
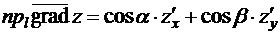 .
.
Правая часть этого равенства в силу Теоремы 1 есть производная по направле-нию. Теорема доказана.
Следствие 1. Производная функции 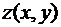 в точке
в точке 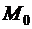 по направлению оси
по направлению оси 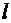 достигает максимума, когда это направление совпадает с градиентом функции, причём
достигает максимума, когда это направление совпадает с градиентом функции, причём
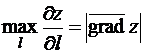 .
.
Таким образом, градиент функции в данной точке характеризует направление и величину максимальной скорости возрастания функции в данной точке.
Следствие 2. Производная функции по направлению, перпендикулярному её градиенту, равна нулю.



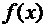 характеризует скорость изменения функции в данной точке в направлении оси
характеризует скорость изменения функции в данной точке в направлении оси 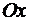 . В двумерном случае частные производные функции
. В двумерном случае частные производные функции 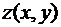 характеризуют то же самое в направлении координатных осей.
характеризуют то же самое в направлении координатных осей.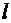 .
.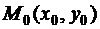 и пусть ось
и пусть ось 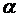 и
и 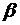 , которые она составляет с осями координат. Ось удобно задавать её ортом:
, которые она составляет с осями координат. Ось удобно задавать её ортом: 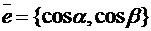 . Будем считать, что ось проходит через точку
. Будем считать, что ось проходит через точку 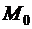 и пусть точка
и пусть точка 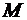 – произвольная точка, лежащая на оси. Тогда
– произвольная точка, лежащая на оси. Тогда 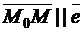 , т.е.
, т.е. 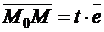 .
.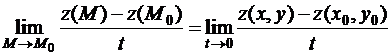 (1)
(1)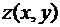 по направлению оси
по направлению оси 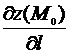 ,
, 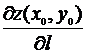 ,
, 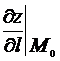 .
. . (2)
. (2)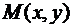 – текущая точка оси
– текущая точка оси 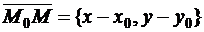 , а
, а 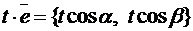 и в силу того, что
и в силу того, что 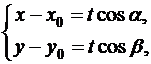
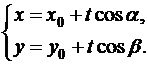
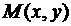 есть функции параметра
есть функции параметра 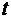 . Тогда:
. Тогда: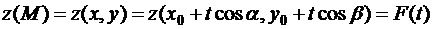 ,
, 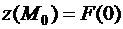
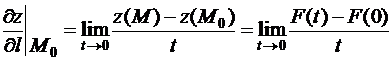 . (3)
. (3)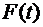 в нуле. Производная же сложной функции
в нуле. Производная же сложной функции 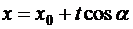 и
и 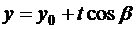 – дифферен-цируемы, при этом:
– дифферен-цируемы, при этом: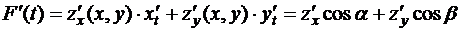 .
.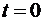 и получим
и получим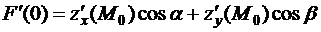 .
.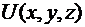 и оси
и оси 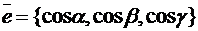 формула (2) приобретает вид
формула (2) приобретает вид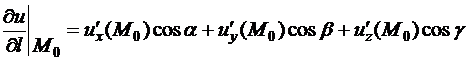 .
.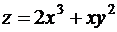 в точке
в точке 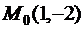 по направлению вектора
по направлению вектора 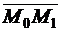 , где
, где 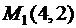 .
.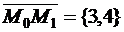 ,
, 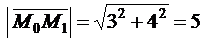 ,
, 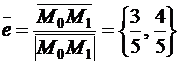 ,
,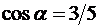 ,
, 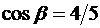 . Далее, вычислим частные производные данной функции в точке
. Далее, вычислим частные производные данной функции в точке 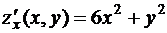 ,
, 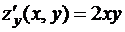 , откуда
, откуда 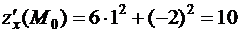 ,
, 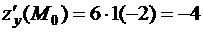 . Теперь по формуле (2) получим
. Теперь по формуле (2) получим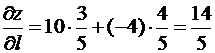 .
.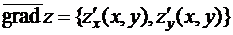 .
.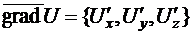 .
.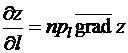 .
. .
.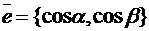 и
и 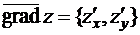 , причём
, причём 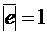 , получим:
, получим: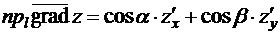 .
.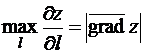 .
.


